人教版七年级数学上册1.3.2.1有理数的减法 教学课件(共27张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.3.2.1有理数的减法 教学课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 275.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 19:21:18 | ||
图片预览





文档简介
(共27张PPT)
1.3.2.1
有理数的减法
第一章
有理数
人教版七年级数学上册
有理数的加法法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
新课导入
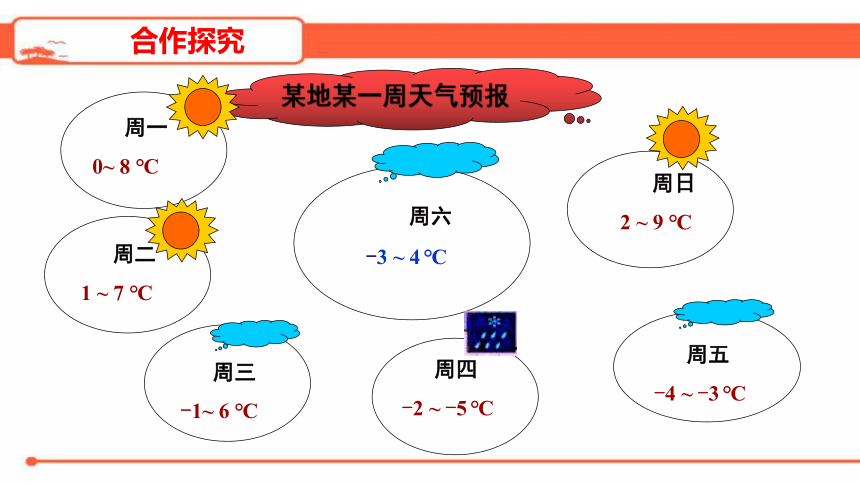
某地某一周天气预报
周三
-1~
6
℃
周五
-4
~
-3
℃
周一
0~
8
℃
周六
-3
~
4
℃
周二
1
~
7
℃
周四
-2
~
-5
℃
周日
2
~
9
℃
合作探究
周六
-3
~
4
℃
0
1
2
3
-1
-2
-3
-4
4
7
你能从温度计看出
4
℃比
–
3
℃高多少度吗?
4-(-3)=
?
合作探究
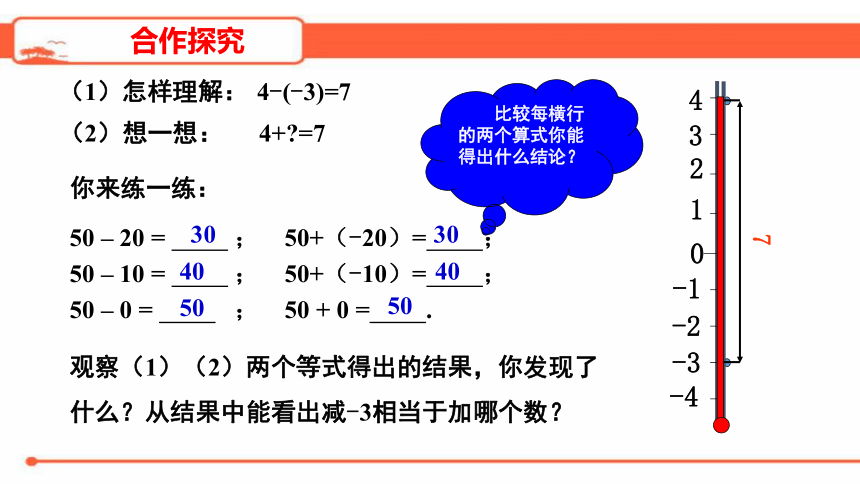
(1)怎样理解:
(2)想一想:
7
你来练一练:
50
–
20
=
;
50+(-20)=
;
50
–
10
=
;
50+(-10)=
;
50
–
0
=
;
50
+
0
=
.
30
30
40
40
50
50
0
1
2
3
-1
-2
-4
4
-3
4-(-3)=7
4+?=7
观察(1)(2)两个等式得出的结果,你发现了什么?从结果中能看出减-3相当于加哪个数?
比较每横行的两个算式你能得出什么结论?
合作探究
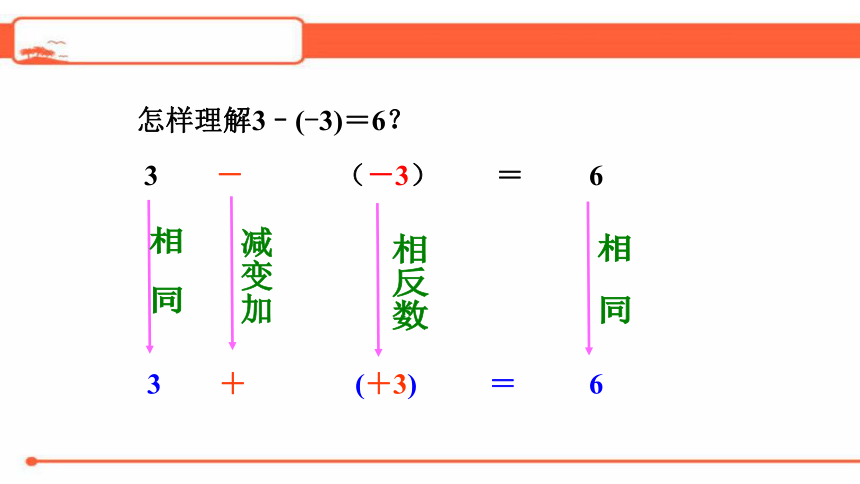
怎样理解3–(-3)=6?
3
-
(-3)
=
6
3
+
(+3)
=
6
相 同
减变加
相反数
相 同
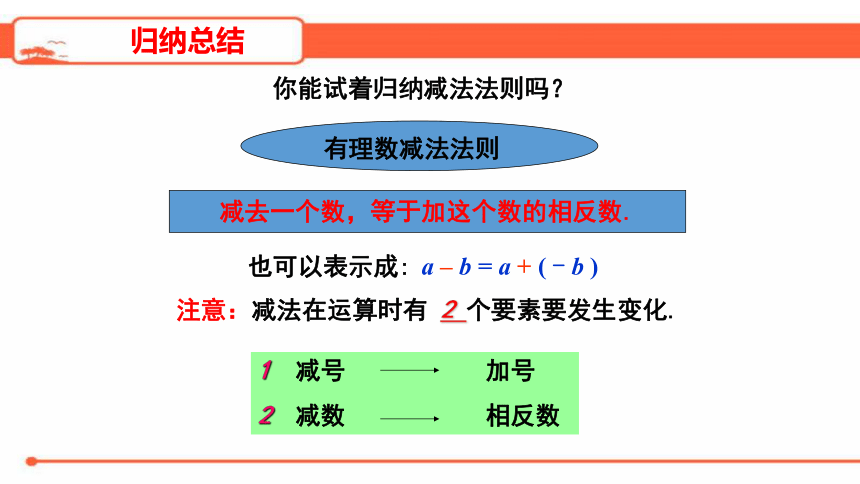
你能试着归纳减法法则吗?
有理数减法法则
减去一个数,等于加这个数的相反数.
也可以表示成:
a
–
b
=
a
+
(
-
b
)
注意:减法在运算时有
2
个要素要发生变化.
1
减号
加号
2
减数
相反数
归纳总结
有理数减法法则:减去一个数,等于加这个数的
相反数;即:a-b=a+(-b).
这里a和b可以
是正,也可以
是负,还可以
为0
由此可见,有理数的减法运算实质转化为加法运算.
转化的思想方法
减法运算步骤:
(1)变减法运算为加法运算,做到“两变一不变”,
“两变”中一变运算符号,减号变加号;二变减
数,减数变为它的相反数;“一不变”被减数
不变;
(2)运用加法法则进行计算.
例1
计算下列各题:
(1)
9
-(-5)
(2)
(-3)-
1
(3)
7.2
–
(-4.8)
解:(1)9-(-5)=
9
+(+
5)
=
14
减去(-5)等于加
-5
的相反数,变成做加法.
(2)(-3)-
1
=(-3)+(-1)
=
-4
减去1等于加1的相反数,变成做加法.
(3)
7.2
–
(-4.8)
=
7.2
+4.8
=
12
减-4.8等于加4.8
例题精析
例2
计算:(1)
(-3)-(-5).
(2)0-7.
(3)7.2-(-4.8).
(4)
解:(1)
(-3)-(-5)=
(-3)+5=2;
(2)0-7=0+(-7)=-7;
(3)7.2-(-4.8)=7.2+4.8=12;
(4)
例题精析
例2
计算:(1)
(+4.5)-(-2.8);
(2)
(3)
导引:
运用减法法则,把“-”号变“+”号,并把减数变为它的相反数.
解:
(1)(+4.5)-(-2.8)=(+4.5)+(+2.8)=7.3.
例题精析
做有理数减法时,我们必须明确两点:
一是进行有理数减法运算的关键在于利用法则
变减法为加法;
二是有理数减法不能直接进行计算,只有转化
为加法后才能进行计算.
例题精析
例3
比较-
与-
的大小.
导引:有理数大小比较中我们介绍了作差比较大
小,并且应用作差比较法比较了两个正数
的大小;这种方法对于两个负数同样适用.
解:
例题精析
两分数大小非常接近时,常用作差法比较大小,
对于任意两个有理数a、b有:
(1)a-b>0?a>b;
(2)a-b=0?a=b;
(3)a-b<0?a例题精析
例4
求出下列每对数在数轴上对应点之间的距离及
这两数的差:
(1)3与-2;(2)4
与2
;(3)-4与4;
(4)-5与-2.
你能发现所得的距离与这两数的差有什么关
系吗?
导引:先在数轴上求出给定的表示两数的点之间的距离.
例题精析
解:(1)3-(-2)=5,对应点之间的距离为5.
(2)4
-2
=2
,对应点之间的距离为2
.
(3)(-4)-4=-8,对应点之间的距离为8.
(4)-5-(-2)=-3,对应点之间的距离为3.
发现:所得的距离与这两数的差的绝对值相等.
例题精析
1.求数轴上两点间的距离的方法:一可利用数轴求.二可利用数轴上两点间的距离公式求(绝对值中阅读题中的结论);
2.数轴上两点间的距离公式:数轴上两点之间的距离等于这两点表示的两个数之差的绝对值.
例题精析
例5
王明同学连续记录了一周内每天的最高气温
和
最低气温,其数据如下表(单位:℃):
星期
一
二
三
四
五
六
日
最高气温
-3
6
8
-2
5
3
11
最低气温
-9
-4
-3
-13
-4
-6
-1
由表中数据分析
:本周内气温最高是多少?气温
最低是多少?哪天的温差最大?温差最大是多少?
例题精析
导引:温差最大即温度差的绝对值最大.
解:本周内气温最高是11
℃,
气温最低是-13
℃,周日的温差最大,
温差最大是11-(-1)=12(℃).
例题精析
2.
计算:1-
=( )
A. B.- C. D.-
1.
在下列括号中填上适当的数.
(1)(-8)-(-6)=(-8)+(________);
(2)(-3)-4=(-3)+(________);
(3)0-
=0+(________);
(4)8-2
020=8+(________).
6
-4
-2020
C
课堂精练
3.
与(-x)-(-y)相等的式子是( )
A.(-x)-(+y)
B.(+x)+(-y)
C.(-x)+y
D.(+x)-(-y)
C
4.
若a为负数,则a减去它的相反数等于( )
A.0
B.2a
C.-2a
D.2a或-2a
5.
若m<0,则|m-(-m)|等于( )
A.2m
B.-2m
C.2m或-2m
D.以上都有可能
B
B
课堂精练
6.
有理数a,b在数轴上所对应的点的位置如图所示,则a-b的值在( )
?A.-3与-2之间
B.-2与-1之间
C.0与1之间
D.2与3之间
D
7.
桂林冬季里某一天最高气温是7
℃,最低气温是-1
℃,这一天桂林的温差是( )
A.-8
℃
B.6
℃
C.7
℃
D.8
℃
D
课堂精练
8.
较小的数减去较大的数,所得的数一定是(
)
A
.
0
B
.
正数
C
.
负数
D
.
0或负数
9.
下列说法正确的是(
)
A
.
减去一个负数,差一定大于被减数
B
.
减去一个正数,差不一定小于被减数
C
.
0减去任何数,差都是负数
D
.
两个数之差一定小于被减数
C
A
课堂精练
10.
下列说法正确的是(
)
A
.
减去一个数,等于加上这个数
B
.
有理数的减法中,被减数不一定比减数大
C
.
0减去一个数
,仍得这个数
D
.
两个相反数相减得
0
11.
差是-5,被减数是-2,则减数为(
)
A
.
-7
B
.
-3
C
.
3
D
.
7
B
C
课堂精练
通过本节课的探讨学习,你获得哪些新知识?
1.
有理数的减法法则是什么?
2.
进行有理数的减法运算时需要注意哪几个步骤?
减去一个数,等于加这个数的相反数.
1
减号
加号
2
减数
相反数
课堂小结
有理数减法法则的实质是将减法转化为加法,
其转化的方法是“两变”:
一是“变”减号为加号;
二是将减数“变”为它的相反数.
课堂小结
1.3.2.1
有理数的减法
第一章
有理数
人教版七年级数学上册
有理数的加法法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
新课导入
某地某一周天气预报
周三
-1~
6
℃
周五
-4
~
-3
℃
周一
0~
8
℃
周六
-3
~
4
℃
周二
1
~
7
℃
周四
-2
~
-5
℃
周日
2
~
9
℃
合作探究
周六
-3
~
4
℃
0
1
2
3
-1
-2
-3
-4
4
7
你能从温度计看出
4
℃比
–
3
℃高多少度吗?
4-(-3)=
?
合作探究
(1)怎样理解:
(2)想一想:
7
你来练一练:
50
–
20
=
;
50+(-20)=
;
50
–
10
=
;
50+(-10)=
;
50
–
0
=
;
50
+
0
=
.
30
30
40
40
50
50
0
1
2
3
-1
-2
-4
4
-3
4-(-3)=7
4+?=7
观察(1)(2)两个等式得出的结果,你发现了什么?从结果中能看出减-3相当于加哪个数?
比较每横行的两个算式你能得出什么结论?
合作探究
怎样理解3–(-3)=6?
3
-
(-3)
=
6
3
+
(+3)
=
6
相 同
减变加
相反数
相 同
你能试着归纳减法法则吗?
有理数减法法则
减去一个数,等于加这个数的相反数.
也可以表示成:
a
–
b
=
a
+
(
-
b
)
注意:减法在运算时有
2
个要素要发生变化.
1
减号
加号
2
减数
相反数
归纳总结
有理数减法法则:减去一个数,等于加这个数的
相反数;即:a-b=a+(-b).
这里a和b可以
是正,也可以
是负,还可以
为0
由此可见,有理数的减法运算实质转化为加法运算.
转化的思想方法
减法运算步骤:
(1)变减法运算为加法运算,做到“两变一不变”,
“两变”中一变运算符号,减号变加号;二变减
数,减数变为它的相反数;“一不变”被减数
不变;
(2)运用加法法则进行计算.
例1
计算下列各题:
(1)
9
-(-5)
(2)
(-3)-
1
(3)
7.2
–
(-4.8)
解:(1)9-(-5)=
9
+(+
5)
=
14
减去(-5)等于加
-5
的相反数,变成做加法.
(2)(-3)-
1
=(-3)+(-1)
=
-4
减去1等于加1的相反数,变成做加法.
(3)
7.2
–
(-4.8)
=
7.2
+4.8
=
12
减-4.8等于加4.8
例题精析
例2
计算:(1)
(-3)-(-5).
(2)0-7.
(3)7.2-(-4.8).
(4)
解:(1)
(-3)-(-5)=
(-3)+5=2;
(2)0-7=0+(-7)=-7;
(3)7.2-(-4.8)=7.2+4.8=12;
(4)
例题精析
例2
计算:(1)
(+4.5)-(-2.8);
(2)
(3)
导引:
运用减法法则,把“-”号变“+”号,并把减数变为它的相反数.
解:
(1)(+4.5)-(-2.8)=(+4.5)+(+2.8)=7.3.
例题精析
做有理数减法时,我们必须明确两点:
一是进行有理数减法运算的关键在于利用法则
变减法为加法;
二是有理数减法不能直接进行计算,只有转化
为加法后才能进行计算.
例题精析
例3
比较-
与-
的大小.
导引:有理数大小比较中我们介绍了作差比较大
小,并且应用作差比较法比较了两个正数
的大小;这种方法对于两个负数同样适用.
解:
例题精析
两分数大小非常接近时,常用作差法比较大小,
对于任意两个有理数a、b有:
(1)a-b>0?a>b;
(2)a-b=0?a=b;
(3)a-b<0?a
例4
求出下列每对数在数轴上对应点之间的距离及
这两数的差:
(1)3与-2;(2)4
与2
;(3)-4与4;
(4)-5与-2.
你能发现所得的距离与这两数的差有什么关
系吗?
导引:先在数轴上求出给定的表示两数的点之间的距离.
例题精析
解:(1)3-(-2)=5,对应点之间的距离为5.
(2)4
-2
=2
,对应点之间的距离为2
.
(3)(-4)-4=-8,对应点之间的距离为8.
(4)-5-(-2)=-3,对应点之间的距离为3.
发现:所得的距离与这两数的差的绝对值相等.
例题精析
1.求数轴上两点间的距离的方法:一可利用数轴求.二可利用数轴上两点间的距离公式求(绝对值中阅读题中的结论);
2.数轴上两点间的距离公式:数轴上两点之间的距离等于这两点表示的两个数之差的绝对值.
例题精析
例5
王明同学连续记录了一周内每天的最高气温
和
最低气温,其数据如下表(单位:℃):
星期
一
二
三
四
五
六
日
最高气温
-3
6
8
-2
5
3
11
最低气温
-9
-4
-3
-13
-4
-6
-1
由表中数据分析
:本周内气温最高是多少?气温
最低是多少?哪天的温差最大?温差最大是多少?
例题精析
导引:温差最大即温度差的绝对值最大.
解:本周内气温最高是11
℃,
气温最低是-13
℃,周日的温差最大,
温差最大是11-(-1)=12(℃).
例题精析
2.
计算:1-
=( )
A. B.- C. D.-
1.
在下列括号中填上适当的数.
(1)(-8)-(-6)=(-8)+(________);
(2)(-3)-4=(-3)+(________);
(3)0-
=0+(________);
(4)8-2
020=8+(________).
6
-4
-2020
C
课堂精练
3.
与(-x)-(-y)相等的式子是( )
A.(-x)-(+y)
B.(+x)+(-y)
C.(-x)+y
D.(+x)-(-y)
C
4.
若a为负数,则a减去它的相反数等于( )
A.0
B.2a
C.-2a
D.2a或-2a
5.
若m<0,则|m-(-m)|等于( )
A.2m
B.-2m
C.2m或-2m
D.以上都有可能
B
B
课堂精练
6.
有理数a,b在数轴上所对应的点的位置如图所示,则a-b的值在( )
?A.-3与-2之间
B.-2与-1之间
C.0与1之间
D.2与3之间
D
7.
桂林冬季里某一天最高气温是7
℃,最低气温是-1
℃,这一天桂林的温差是( )
A.-8
℃
B.6
℃
C.7
℃
D.8
℃
D
课堂精练
8.
较小的数减去较大的数,所得的数一定是(
)
A
.
0
B
.
正数
C
.
负数
D
.
0或负数
9.
下列说法正确的是(
)
A
.
减去一个负数,差一定大于被减数
B
.
减去一个正数,差不一定小于被减数
C
.
0减去任何数,差都是负数
D
.
两个数之差一定小于被减数
C
A
课堂精练
10.
下列说法正确的是(
)
A
.
减去一个数,等于加上这个数
B
.
有理数的减法中,被减数不一定比减数大
C
.
0减去一个数
,仍得这个数
D
.
两个相反数相减得
0
11.
差是-5,被减数是-2,则减数为(
)
A
.
-7
B
.
-3
C
.
3
D
.
7
B
C
课堂精练
通过本节课的探讨学习,你获得哪些新知识?
1.
有理数的减法法则是什么?
2.
进行有理数的减法运算时需要注意哪几个步骤?
减去一个数,等于加这个数的相反数.
1
减号
加号
2
减数
相反数
课堂小结
有理数减法法则的实质是将减法转化为加法,
其转化的方法是“两变”:
一是“变”减号为加号;
二是将减数“变”为它的相反数.
课堂小结
