沪教版八年级数学上册18.1 函数的概念课件(共18张PPT)
文档属性
| 名称 | 沪教版八年级数学上册18.1 函数的概念课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 18:35:33 | ||
图片预览





文档简介
(共18张PPT)
18.1
函数的概念
问题1
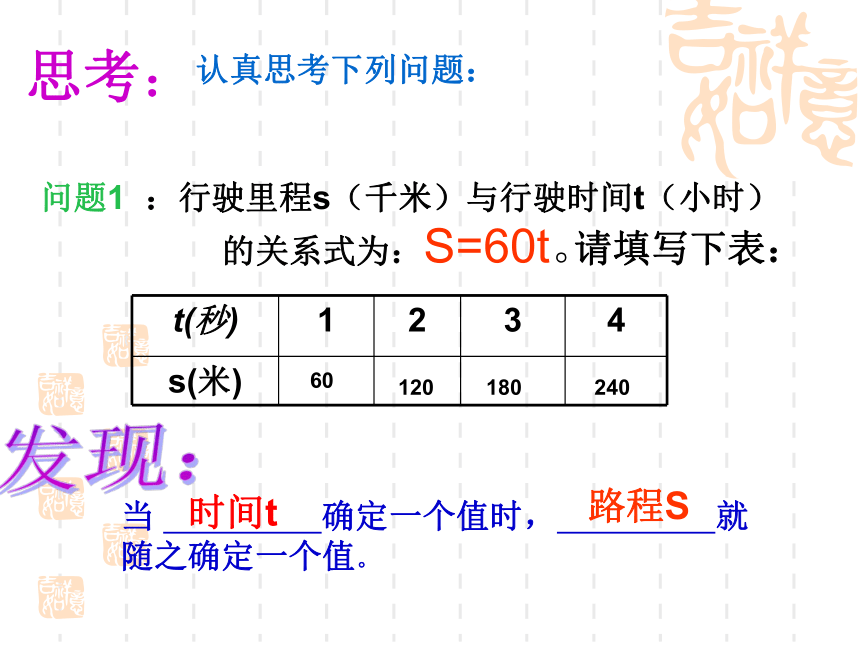
:行驶里程s(千米)与行驶时间t(小时)的关系式为:S=60t。
当
确定一个值时,
就随之确定一个值。
时间t
路程S
t(秒)
1
2
3
4
s(米)
认真思考下列问题:
60
120
240
180
发现:
思考:
请填写下表:
问题2
票房收入y元与售票数量x张的关系式:
y=10x
X=150时
y=1500;
X=205时
y=2050;
当________确定一个值时,_______就随之确定一个值。
售票数量x
票房收入y
发现:
L=10+0.5m
问题3
重物质量
m(Kg)
1
2
3
4
5
弹簧长度
L(cm)
10.5
11
11.5
12
12.5
用含重物质量m(kg)的式子表示受力后的
弹簧长度
L(cm)为:
当
确定一个值时,
就随之确定一个值。
重物质量m
弹簧长度L
发现:
问题4
圆的半径r
与圆的面积s的关系式:
计算:
S=10
时,r=_
_
_
cm
S=20
时,r=
_
_
_
cm
当
_____确定一个值时,_____随之就确定一个值。
面积s
半径r
发现:
一边长为X(m)
4
3
2.5
2
…
另一边长为
(
)(m)
…
长方形面积s(m2)
…
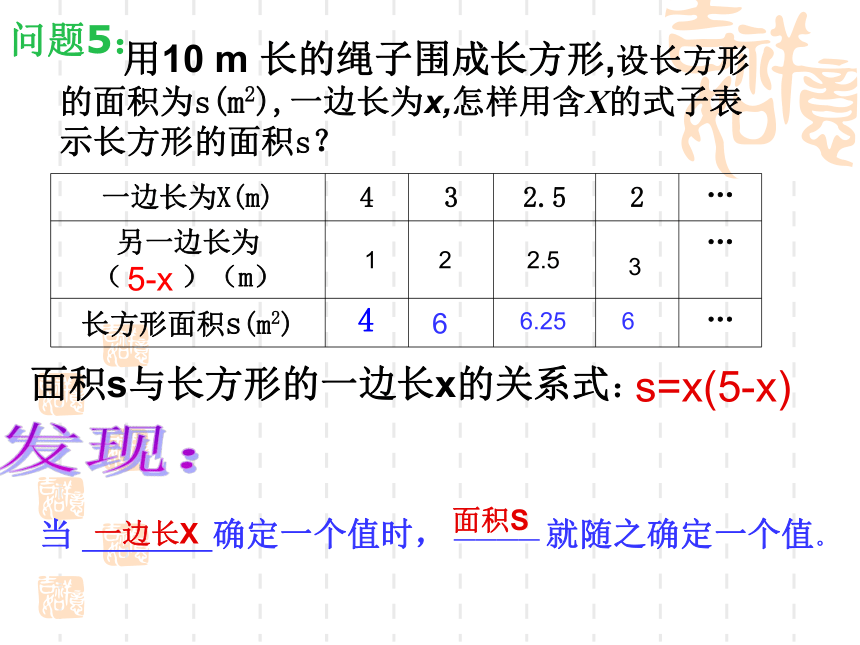
用10
m
长的绳子围成长方形,设长方形的面积为s(m2),一边长为x,怎样用含X的式子表示长方形的面积s?
问题5:
4
1
2
2.5
3
6
6.25
6
5-x
s=x(5-x)
当
确定一个值时,
————
就随之确定一个值。
一边长X
面积S
面积s与长方形的一边长x的关系式:
发现:
归纳
2
两个变量互相联系,当其中一个
变量确定一个值时,另一个变量就(
)。
1
每个变化的过程中都存在着(
)变量.
两个
有唯一确定的值与其对应
(1)下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
o
x
y
思考
(2)在下面的我国人口数统计表中,年份与人口数
可以记作两个变量x与y,对于表中每一个确定的年
份(x),都对应着一个确定的人口数(y)吗?
函数的概念:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
思考:上面五个问题中哪些是自变量,哪些是自变量的函数?
在一个变化过程中,
如果有两个变量x与y,
并且对于x的每一个确定的值,y都有唯
一确定的值与其对应,
那么我们就说x是自变量
,
y是x的函数。
S
=
60
t
L
=
10+0.5m
y
=
10x
S
=
x(5-x)
探究与讨论
(1)在计算器上按照下面的程序进行操作:
输入x(任意一个数)
按键
×
2
+
5
=
显示y(计算结果)
x
1
3
-4
0
101
y
7
11
-3
5
207
问题:显示的数y是x的函数吗?为什么?
y是x的函数,因为x取定一个值时,y都有唯一确定的值与其对应。
上面操作程序中所按的第三个键和第四个键
应是
.
2、在计算器上按照下面的程序进行操作:
?
下表中的x与y分别是输入的6个数及相应的计算结果:
x
-2
-1
0
1
2
3
y
-5
-2
1
4
7
10
+
1
y是X的函数吗?若是,写出它的表达式(用含X的式子表示y).
是。y=3x+1
要考虑实际意义哦!
例1
一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1)写出表示y与x的函数关系的式子。
(2)指出自变量x的取值范围;
(3)汽车行驶200
km时,油箱中还有多少油?
解:(1)
函数关系式为:
y
=
50-0.1x
(2)
由
x≥0
0.1x
≤
50
∴自变量的取值范围是:
0
≤
x
≤
500
(3)把x
=
200代入
y
=50
-0.1x得
:
因此,当汽车行驶200
km时,油箱中还有油30L。
解得 0
≤
x
≤
500
这样的式子叫做函数解析式。
y=50-0.1×200=30
例题反思:
确定自变量的取值范围时,不仅要考虑
函数关系式有意义,而且还要注意问题的实际意义。
1.下列各式中,x是自变量,请判断y
是不是x的函数?若是,求出自变量的取值范围。
3.y=
+
1
x
4.y=
1.y=
2x
2.y=
解:1
y是x的函数。
2、y是x的函数。
∵X-3
≥0∴x
≥3.
3、y不是x的函数。
4、y是x的函数.
x≠0.
X为全体实数。
对于x的每一个值,y总有唯一确定的值与它对应,y才是x的函数。
当堂训练
2.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子。
(1)改变正方形的边长X,正方形的面积S随之改变。
(2)秀水村的耕地面积是106
,这个村人均占有耕地面积y随这个村人数n的变化而变化。
m2
____是自变量,___
是___的函数,
关系式__________。
___是自变量,___是___的函数,
关系式____________。
x
s
x
S=x2
n
y
n
通过这节课的学习,你有什么收获?
用60m的篱笆围成
矩形,使矩形一边靠墙,
另三边用篱笆围成。
(1).写出矩形面积s(m2)与平行于墙的一边长a(m)的关系式;
(2).写出矩形面积s(m2)与垂直于墙的一边长b(m)的关系式。并指出两式中的函数与自变量。
墙
a
b
b
60-a
2
S=a
S=(60-2b)b
18.1
函数的概念
问题1
:行驶里程s(千米)与行驶时间t(小时)的关系式为:S=60t。
当
确定一个值时,
就随之确定一个值。
时间t
路程S
t(秒)
1
2
3
4
s(米)
认真思考下列问题:
60
120
240
180
发现:
思考:
请填写下表:
问题2
票房收入y元与售票数量x张的关系式:
y=10x
X=150时
y=1500;
X=205时
y=2050;
当________确定一个值时,_______就随之确定一个值。
售票数量x
票房收入y
发现:
L=10+0.5m
问题3
重物质量
m(Kg)
1
2
3
4
5
弹簧长度
L(cm)
10.5
11
11.5
12
12.5
用含重物质量m(kg)的式子表示受力后的
弹簧长度
L(cm)为:
当
确定一个值时,
就随之确定一个值。
重物质量m
弹簧长度L
发现:
问题4
圆的半径r
与圆的面积s的关系式:
计算:
S=10
时,r=_
_
_
cm
S=20
时,r=
_
_
_
cm
当
_____确定一个值时,_____随之就确定一个值。
面积s
半径r
发现:
一边长为X(m)
4
3
2.5
2
…
另一边长为
(
)(m)
…
长方形面积s(m2)
…
用10
m
长的绳子围成长方形,设长方形的面积为s(m2),一边长为x,怎样用含X的式子表示长方形的面积s?
问题5:
4
1
2
2.5
3
6
6.25
6
5-x
s=x(5-x)
当
确定一个值时,
————
就随之确定一个值。
一边长X
面积S
面积s与长方形的一边长x的关系式:
发现:
归纳
2
两个变量互相联系,当其中一个
变量确定一个值时,另一个变量就(
)。
1
每个变化的过程中都存在着(
)变量.
两个
有唯一确定的值与其对应
(1)下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
o
x
y
思考
(2)在下面的我国人口数统计表中,年份与人口数
可以记作两个变量x与y,对于表中每一个确定的年
份(x),都对应着一个确定的人口数(y)吗?
函数的概念:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
思考:上面五个问题中哪些是自变量,哪些是自变量的函数?
在一个变化过程中,
如果有两个变量x与y,
并且对于x的每一个确定的值,y都有唯
一确定的值与其对应,
那么我们就说x是自变量
,
y是x的函数。
S
=
60
t
L
=
10+0.5m
y
=
10x
S
=
x(5-x)
探究与讨论
(1)在计算器上按照下面的程序进行操作:
输入x(任意一个数)
按键
×
2
+
5
=
显示y(计算结果)
x
1
3
-4
0
101
y
7
11
-3
5
207
问题:显示的数y是x的函数吗?为什么?
y是x的函数,因为x取定一个值时,y都有唯一确定的值与其对应。
上面操作程序中所按的第三个键和第四个键
应是
.
2、在计算器上按照下面的程序进行操作:
?
下表中的x与y分别是输入的6个数及相应的计算结果:
x
-2
-1
0
1
2
3
y
-5
-2
1
4
7
10
+
1
y是X的函数吗?若是,写出它的表达式(用含X的式子表示y).
是。y=3x+1
要考虑实际意义哦!
例1
一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1)写出表示y与x的函数关系的式子。
(2)指出自变量x的取值范围;
(3)汽车行驶200
km时,油箱中还有多少油?
解:(1)
函数关系式为:
y
=
50-0.1x
(2)
由
x≥0
0.1x
≤
50
∴自变量的取值范围是:
0
≤
x
≤
500
(3)把x
=
200代入
y
=50
-0.1x得
:
因此,当汽车行驶200
km时,油箱中还有油30L。
解得 0
≤
x
≤
500
这样的式子叫做函数解析式。
y=50-0.1×200=30
例题反思:
确定自变量的取值范围时,不仅要考虑
函数关系式有意义,而且还要注意问题的实际意义。
1.下列各式中,x是自变量,请判断y
是不是x的函数?若是,求出自变量的取值范围。
3.y=
+
1
x
4.y=
1.y=
2x
2.y=
解:1
y是x的函数。
2、y是x的函数。
∵X-3
≥0∴x
≥3.
3、y不是x的函数。
4、y是x的函数.
x≠0.
X为全体实数。
对于x的每一个值,y总有唯一确定的值与它对应,y才是x的函数。
当堂训练
2.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子。
(1)改变正方形的边长X,正方形的面积S随之改变。
(2)秀水村的耕地面积是106
,这个村人均占有耕地面积y随这个村人数n的变化而变化。
m2
____是自变量,___
是___的函数,
关系式__________。
___是自变量,___是___的函数,
关系式____________。
x
s
x
S=x2
n
y
n
通过这节课的学习,你有什么收获?
用60m的篱笆围成
矩形,使矩形一边靠墙,
另三边用篱笆围成。
(1).写出矩形面积s(m2)与平行于墙的一边长a(m)的关系式;
(2).写出矩形面积s(m2)与垂直于墙的一边长b(m)的关系式。并指出两式中的函数与自变量。
墙
a
b
b
60-a
2
S=a
S=(60-2b)b
