人教版数学八年级上册 13.3.2 等边三角形课件 (共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.2 等边三角形课件 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 19:30:52 | ||
图片预览




文档简介
(共25张PPT)
13.3.2等边三角形
学习目标
掌握等边三角形的定义
掌握等边三角形的性质
掌握等边三角形的判定
掌握直角三角形中30°所对直角边与斜边的关系
如图
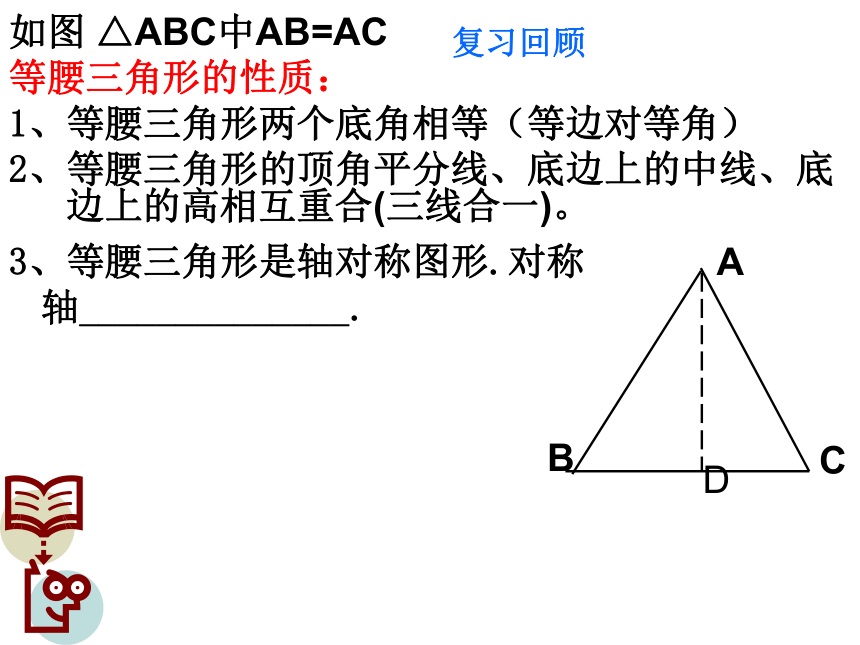
△ABC中AB=AC
等腰三角形的性质:
1、等腰三角形两个底角相等(等边对等角)
2、等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一)。
D
C
B
A
3、等腰三角形是轴对称图形.对称轴______________.
复习回顾
O
A
B
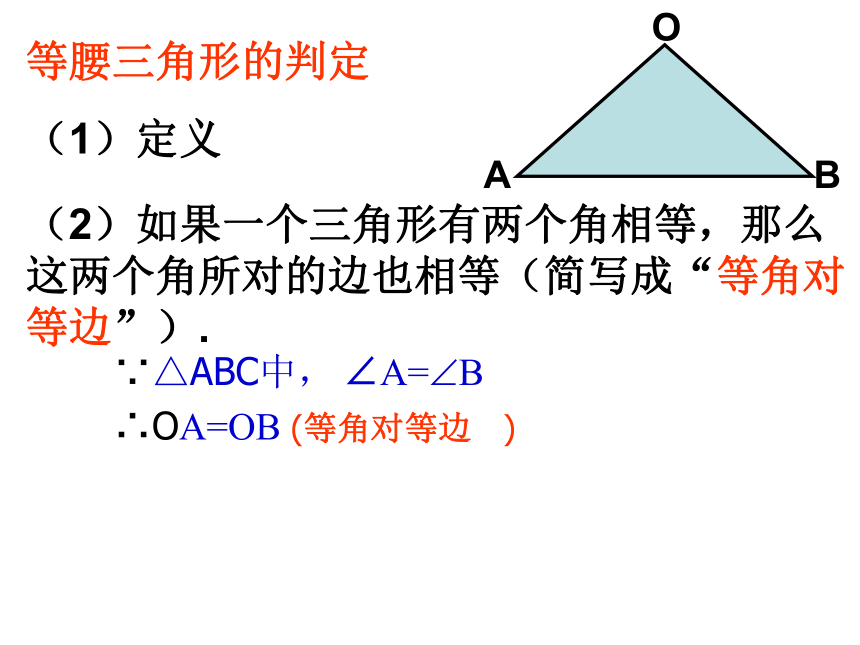
(2)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
∴OA=OB
(等角对等边
)
∵△ABC中,
∠A=?B
等腰三角形的判定
(1)定义
O
A
B
C
M
N
角平分线+平行
等腰三角形
1
2
3
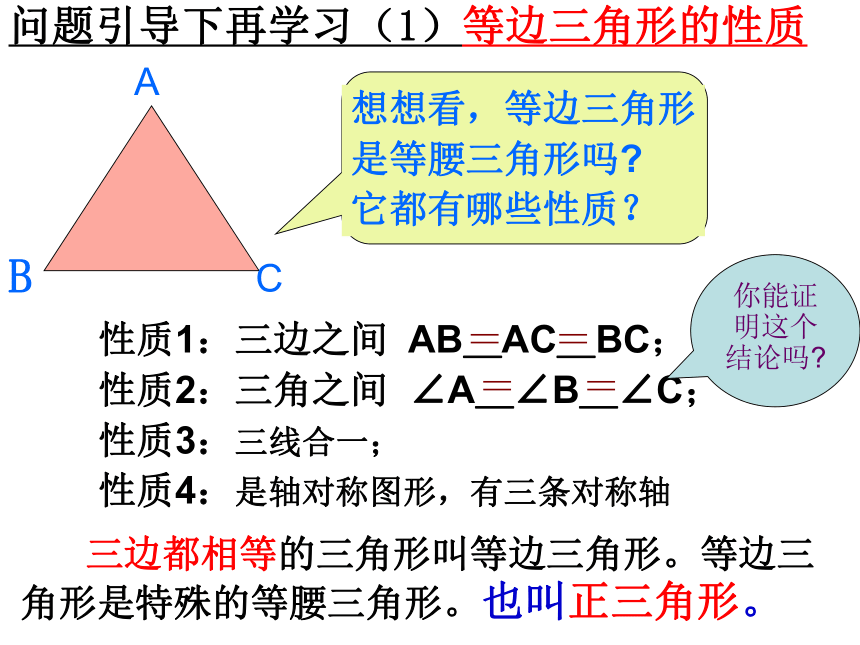
想想看,等边三角形
是等腰三角形吗?
它都有哪些性质?
性质1:三边之间
AB_AC_BC;
性质2:三角之间
∠A_∠B_∠C;
性质3:三线合一;
性质4:是轴对称图形,有三条对称轴
=
=
=
=
你能证明这个结论吗?
问题引导下再学习(1)等边三角形的性质
A
C
B
三边都相等的三角形叫等边三角形。等边三角形是特殊的等腰三角形。也叫正三角形。
A
B
C
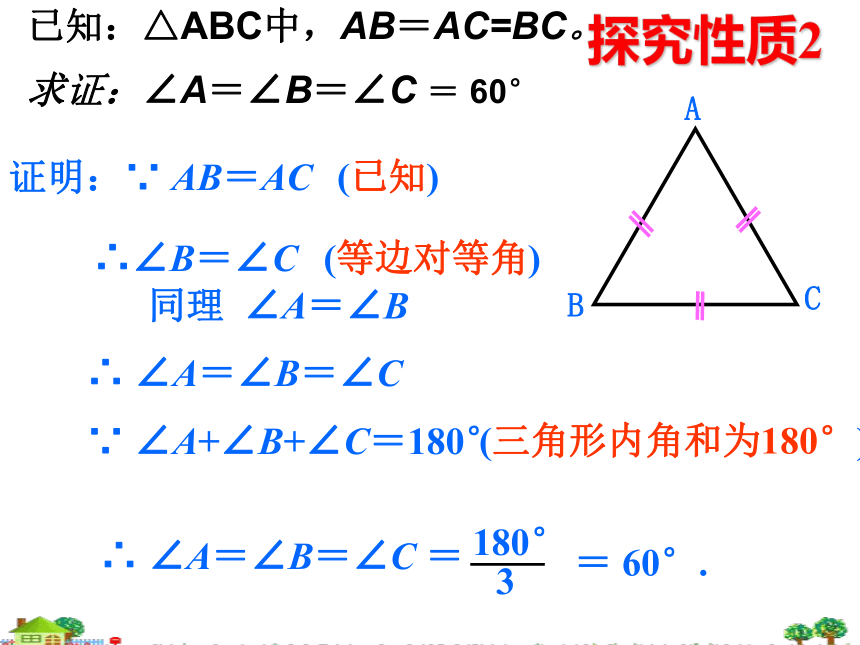
证明:∵
AB=AC
∵
∠A+∠B+∠C=180°
∴
∠A=∠B=∠C
=
∴∠B=∠C
同理
∠A=∠B
∴
∠A=∠B=∠C
180°
3
=
60°.
(等边对等角)
(已知)
(三角形内角和为180°)
已知:△ABC中,AB=AC=BC。
求证:∠A=∠B=∠C
=
60°
探究性质2
归纳
思考题
?
一个三角形满足什么条件
就是等边三角形?
问题引导下再学习(2)等边三角形的判定
方法1:有两边相等的三角形是等腰三角形.(定义)
思维链接:
方法2:有两个角相等的三角形是等腰三角形.(定理)
三条边都相等的三角形
是等边三角形(定义)
三个角都相等的三
角形是等边三角形
有一个角是60°的等腰
三角形是等边三角形
满足什么条件的三角形是等边三角形
?
满足什么条件的三角形是等腰三角形?
结合边和角来看,会有什么新的结论吗?
已知:如图,△ABC中,
∠
A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在△ABC中
∵
∠
A=∠B(已知)
∴BC=CA(等角对等边)
同理
CA=AB
∴BC=CA=AB
推论1:
三个角都相等的三角形是等边三角形?
A
B
C
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
判定1:三个角都相等的三角形是等边三角形。
已知:
△ABC中,AB=AC,
∠
A=600。
求证:AB=AC=BC
A
B
C
证明:
△ABC中
∵AB=AC,
∴
∠B=∠C
(等边对等角)
∵
∠
A=600
∴
∠B=∠C
=
600
∴AB=AC=BC(等角对等边)
判定2:(边角综合)
有一个角是
60°的等腰三角形是等边三角形。
A
B
C
∵
∠B=600
AB=BC
∴△ABC是等边三角形
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
1.三边都相等的三角形是等边三角形.(定义)
一般三角形
等边三角形
A
B
C
等腰三角形
等边三角形
A
B
C
∵AB=BC=AC
∴△ABC是等边三角形
∵
∠B=600
AB=BC
∴△ABC是等边三角形
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
等边三角形的判定方法
归纳
当堂训练
1.下列说法中,正确说法的个数为(
)
(1)若等腰三角形有一个角等于60°,则这个三角形为等边三角形
(2)等边三角形一定是等腰三角形,而等腰三角形不一定是等边三角形
(3)有两个角是60°的三角形一定是等边三角形
(4)等边三角形中所有的中线、高、角平分线总条数是3条
A.1个
B.2个
C.3个
D.4个
D
2.如果一个三角形是轴对称图形,且有一个外角是120°,那么这个三角形是(
)
A.直角三角形
B.等腰直角三角形
C.正三角形
D.含30°角的直角三角形
3.如图,△ABC是等边三角形,且∠1=∠2=∠3,则∠D等于(
)
A.90°
B.80°
C.45°
D.60°
A
B
C
D
E
F
1
2
3
C
D
3、
如图,等边三角形ABC中,AD是BC上的高,∠BDE=
∠CDF=60°,结合图形,你能得出哪些结论?
结论:
线:BD=DC=BE=DE=DF=CF
=AF=AE
角:∠ADE=
∠ADF=
∠EAD=
∠DAF=
30°
形:△ADE和△ADF是等腰三角形
△BED和△CFD是等边三角形
其他:DE∥AC,DF∥AB等.
A
C
B
D
E
F
将两个含有30°角的直角三角尺摆放在一起,你能借助这个图形,找出Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
问题引导下再学习(3)含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等30°,
那么它所对的直角边等于斜边的一半。
含30°角的直角三角形的性质
例3右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,
∠A=
30
°,立柱BC、DE要多长?
解:
∵DE⊥AC,BC⊥AC,
∠A=
30
°
∴BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又∵点D是AB的中点
∴AD=1/2AB=3.7(m)
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.
B
A
D
C
E
5如图,在△ABC
中∠C=90°,∠B=15°,AB的垂直平
分线交BC于D,交AB于M,且BD=8㎝,求AC之长.
6等腰三角形的底角为15°,腰长为2a,求腰上的高.
已知:如图,在△ABC中,AB=AC=2a,
∠ABC=∠ACB=15°,
CD
是腰AB上的高。
求:CD的长.
M
C
B
D
A
5题图
6题图
C
4.如图所示,AC=BC=10cm,∠B=15°,
AD⊥BC于点D,则AD的长为
( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
解析:
∵AC=BC,∴∠B=∠BAC=15°,∴∠ACD=∠B+
∠BAC=15°+15°=30°,∵AD⊥BC,∴AD=
AC
=
×10=5(cm).故选C.
等边三角形与等腰三角形异同
定义
性质
判定
等腰
三角形
等边
三角形
有两条边相等
①两边、两角相等
②三线合一
③一条对称轴
①三边、三角相等
②三线合一
③三条对称轴
有三条边相等
①定义
②等角对等边
①定义
②三个角都相等
③等腰三角形有一
个角是60°
关系:等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形.
小结
13.3.2等边三角形
学习目标
掌握等边三角形的定义
掌握等边三角形的性质
掌握等边三角形的判定
掌握直角三角形中30°所对直角边与斜边的关系
如图
△ABC中AB=AC
等腰三角形的性质:
1、等腰三角形两个底角相等(等边对等角)
2、等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一)。
D
C
B
A
3、等腰三角形是轴对称图形.对称轴______________.
复习回顾
O
A
B
(2)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
∴OA=OB
(等角对等边
)
∵△ABC中,
∠A=?B
等腰三角形的判定
(1)定义
O
A
B
C
M
N
角平分线+平行
等腰三角形
1
2
3
想想看,等边三角形
是等腰三角形吗?
它都有哪些性质?
性质1:三边之间
AB_AC_BC;
性质2:三角之间
∠A_∠B_∠C;
性质3:三线合一;
性质4:是轴对称图形,有三条对称轴
=
=
=
=
你能证明这个结论吗?
问题引导下再学习(1)等边三角形的性质
A
C
B
三边都相等的三角形叫等边三角形。等边三角形是特殊的等腰三角形。也叫正三角形。
A
B
C
证明:∵
AB=AC
∵
∠A+∠B+∠C=180°
∴
∠A=∠B=∠C
=
∴∠B=∠C
同理
∠A=∠B
∴
∠A=∠B=∠C
180°
3
=
60°.
(等边对等角)
(已知)
(三角形内角和为180°)
已知:△ABC中,AB=AC=BC。
求证:∠A=∠B=∠C
=
60°
探究性质2
归纳
思考题
?
一个三角形满足什么条件
就是等边三角形?
问题引导下再学习(2)等边三角形的判定
方法1:有两边相等的三角形是等腰三角形.(定义)
思维链接:
方法2:有两个角相等的三角形是等腰三角形.(定理)
三条边都相等的三角形
是等边三角形(定义)
三个角都相等的三
角形是等边三角形
有一个角是60°的等腰
三角形是等边三角形
满足什么条件的三角形是等边三角形
?
满足什么条件的三角形是等腰三角形?
结合边和角来看,会有什么新的结论吗?
已知:如图,△ABC中,
∠
A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在△ABC中
∵
∠
A=∠B(已知)
∴BC=CA(等角对等边)
同理
CA=AB
∴BC=CA=AB
推论1:
三个角都相等的三角形是等边三角形?
A
B
C
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
判定1:三个角都相等的三角形是等边三角形。
已知:
△ABC中,AB=AC,
∠
A=600。
求证:AB=AC=BC
A
B
C
证明:
△ABC中
∵AB=AC,
∴
∠B=∠C
(等边对等角)
∵
∠
A=600
∴
∠B=∠C
=
600
∴AB=AC=BC(等角对等边)
判定2:(边角综合)
有一个角是
60°的等腰三角形是等边三角形。
A
B
C
∵
∠B=600
AB=BC
∴△ABC是等边三角形
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
1.三边都相等的三角形是等边三角形.(定义)
一般三角形
等边三角形
A
B
C
等腰三角形
等边三角形
A
B
C
∵AB=BC=AC
∴△ABC是等边三角形
∵
∠B=600
AB=BC
∴△ABC是等边三角形
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
等边三角形的判定方法
归纳
当堂训练
1.下列说法中,正确说法的个数为(
)
(1)若等腰三角形有一个角等于60°,则这个三角形为等边三角形
(2)等边三角形一定是等腰三角形,而等腰三角形不一定是等边三角形
(3)有两个角是60°的三角形一定是等边三角形
(4)等边三角形中所有的中线、高、角平分线总条数是3条
A.1个
B.2个
C.3个
D.4个
D
2.如果一个三角形是轴对称图形,且有一个外角是120°,那么这个三角形是(
)
A.直角三角形
B.等腰直角三角形
C.正三角形
D.含30°角的直角三角形
3.如图,△ABC是等边三角形,且∠1=∠2=∠3,则∠D等于(
)
A.90°
B.80°
C.45°
D.60°
A
B
C
D
E
F
1
2
3
C
D
3、
如图,等边三角形ABC中,AD是BC上的高,∠BDE=
∠CDF=60°,结合图形,你能得出哪些结论?
结论:
线:BD=DC=BE=DE=DF=CF
=AF=AE
角:∠ADE=
∠ADF=
∠EAD=
∠DAF=
30°
形:△ADE和△ADF是等腰三角形
△BED和△CFD是等边三角形
其他:DE∥AC,DF∥AB等.
A
C
B
D
E
F
将两个含有30°角的直角三角尺摆放在一起,你能借助这个图形,找出Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
问题引导下再学习(3)含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等30°,
那么它所对的直角边等于斜边的一半。
含30°角的直角三角形的性质
例3右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,
∠A=
30
°,立柱BC、DE要多长?
解:
∵DE⊥AC,BC⊥AC,
∠A=
30
°
∴BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又∵点D是AB的中点
∴AD=1/2AB=3.7(m)
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.
B
A
D
C
E
5如图,在△ABC
中∠C=90°,∠B=15°,AB的垂直平
分线交BC于D,交AB于M,且BD=8㎝,求AC之长.
6等腰三角形的底角为15°,腰长为2a,求腰上的高.
已知:如图,在△ABC中,AB=AC=2a,
∠ABC=∠ACB=15°,
CD
是腰AB上的高。
求:CD的长.
M
C
B
D
A
5题图
6题图
C
4.如图所示,AC=BC=10cm,∠B=15°,
AD⊥BC于点D,则AD的长为
( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
解析:
∵AC=BC,∴∠B=∠BAC=15°,∴∠ACD=∠B+
∠BAC=15°+15°=30°,∵AD⊥BC,∴AD=
AC
=
×10=5(cm).故选C.
等边三角形与等腰三角形异同
定义
性质
判定
等腰
三角形
等边
三角形
有两条边相等
①两边、两角相等
②三线合一
③一条对称轴
①三边、三角相等
②三线合一
③三条对称轴
有三条边相等
①定义
②等角对等边
①定义
②三个角都相等
③等腰三角形有一
个角是60°
关系:等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形.
小结
