人教版数学八年级上册 13.3.2等边三角形——含30°角的直角三角形的性质课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.2等边三角形——含30°角的直角三角形的性质课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
13.3.2(2)含30?角的直角三角形的性质
预习检测
1.通过拼图,探素、发现、归纳、证明含30°角的直角三角形的性质.
2.能说出有一个角为30°的直角三角形的性质
并会简单应用.
重点:含30°角的直角三角形的性质定理及应用.
难点:含30°角的直角三角形的性质定理及应用.
学习目标
重点难点
问题引导下再学习
新知探究
探究:如图将两个含30°角的三角尺摆放在一起.你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
A
B
C
D
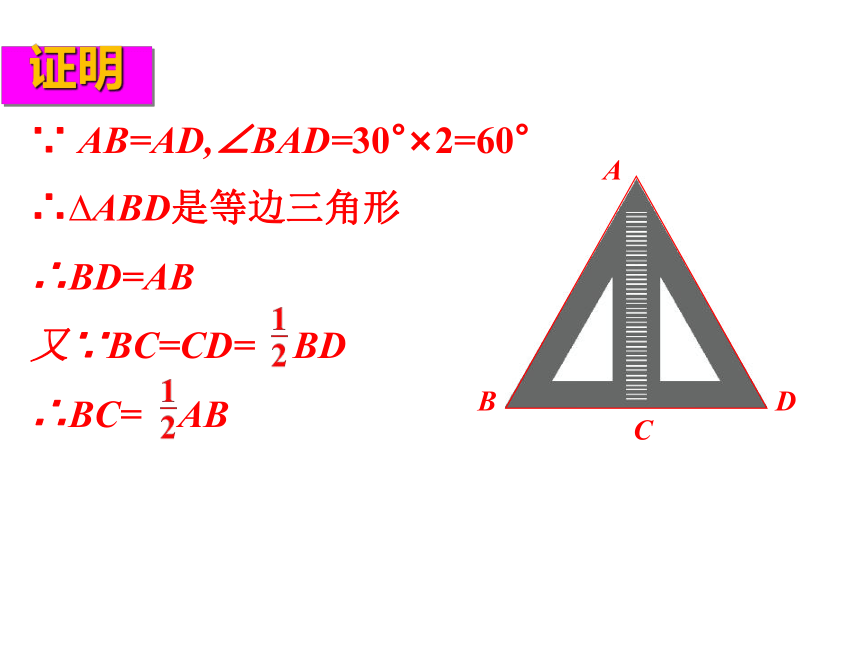
证明
A
B
C
D
∵
AB=AD,∠BAD=30°×2=60°
∴?ABD是等边三角形
∴BD=AB
又∵BC=CD=
BD
∴BC=
AB
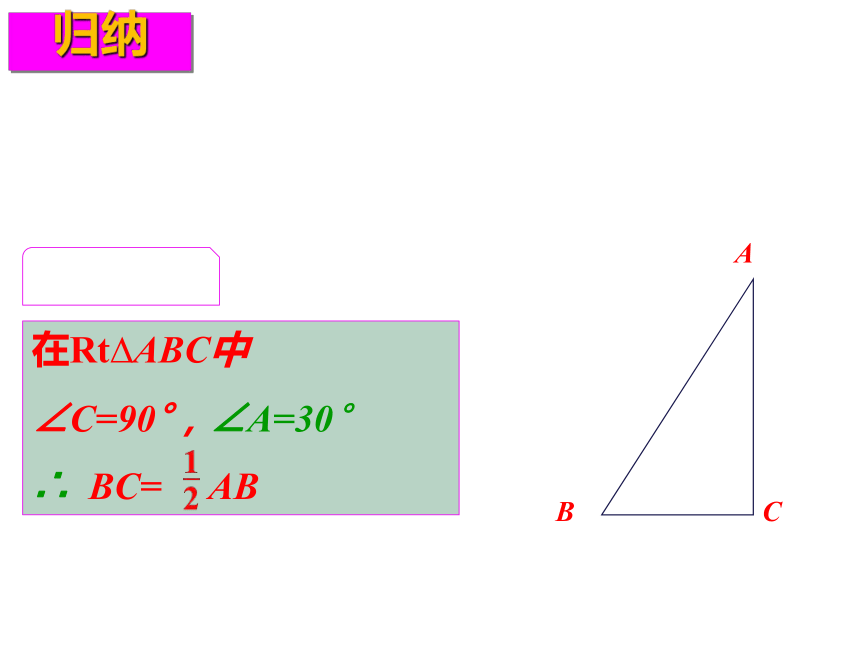
归纳
在直角三角形中,如果一个锐角等于
30°,那么它所对的直角边等于斜边的一半.
A
B
C
几何语言
在Rt?ABC中
∠C=90°,∠A=30°
∴
BC=
AB
当堂训练
1.有一直角三角尺,30°角所对直角边长是6cm,则斜边的长是(
)
A
.3cm
B.
6
cmc
C.10
cm
D.
12
cm
2.如图,在等边三角形ABC中,AB=10cm,D是AB的中点,过点D作DE⊥AC于点E,则EC的长是(
)
A.
2.5
cm
B.
5
cm
C.7
cm
D.
7.5
cm
D
D
A
B
D
E
C
∟
3.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则BD的长是(
).
C
A
B
D
C
∟
4.如图,在Rt△ABC中,∠ACB=90°,∠B=15°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18cm,则AC的长是
.
9cm
A
B
D
C
∟
E
当堂训练
5.如图所示,点P是∠AOB平分线上的一点,过点P作PC∥OA交OB于点C,若∠AOB=30°,OC=4,求点P到OA的距离PD.
A
B
O
D
P
C
∟
E
解:过P作PE⊥OB,如图所示
∵PC∥OA∴∠PCB=∠AOB=30°
∠AOP=∠OPC,
∵OP是∠AOB平分线
∴∠AOP=∠POB,PD=PE,
∴∠POB=∠OPC,
∴CO=PC,
∵OC=4,∴PC=4
∵∠PCB=30°,PE⊥OB,
∴PE=
PC=2,∴PD=2
1
2
归纳总结
利用含30°角的直角三角形的性质解决问题的方法
解题时,一般是先寻找30°角所在的直角三角形,得到斜边与直角边的关系,当30°角不在一个直角三角形中时,可考虑作垂线得到含30°角的直角三角形,或作等腰三角形构造顶角的邻补角为60°.当三角形中含15°,30°,60°,120°角时,也可通过添加辅助线,构造含30°角的直角三角形求解.
达标检测
1.右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,
∠A=
30
°,
则BC=
m、DE=
m.
3.7
1.85
2.如图,一棵树在一次强台风中于离地面3m处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为(
)
A.6
m
B.9
m
C.12m
D.15m
B
30°
3.如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC,AB于点M,N,且BM=3,则CM=
.
6
A
B
M
C
∟
N
达标检测
4.如图所示是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h=_____
m
4
150°
A
B
M
C
D
达标检测
5.如图,已知∠MAN=120°,AC平分∠MAN,B,D分别在射线AN,AM上.
(1)若∠ABC=∠ADC=90°,如图1,求证:AD+AB=AC
A
B
D
N
M
C
∟
∟
图1
达标检测
(2)若∠ABC+∠ADC=180°,如图2,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由
A
B
图2
D
N
M
C
达标检测
课堂小结
直角三角形的性质
1.例2、变式2;
达标2、3;
提能5-8;
2.预习13.4最短路径;
作业布置
13.3.2(2)含30?角的直角三角形的性质
预习检测
1.通过拼图,探素、发现、归纳、证明含30°角的直角三角形的性质.
2.能说出有一个角为30°的直角三角形的性质
并会简单应用.
重点:含30°角的直角三角形的性质定理及应用.
难点:含30°角的直角三角形的性质定理及应用.
学习目标
重点难点
问题引导下再学习
新知探究
探究:如图将两个含30°角的三角尺摆放在一起.你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
A
B
C
D
证明
A
B
C
D
∵
AB=AD,∠BAD=30°×2=60°
∴?ABD是等边三角形
∴BD=AB
又∵BC=CD=
BD
∴BC=
AB
归纳
在直角三角形中,如果一个锐角等于
30°,那么它所对的直角边等于斜边的一半.
A
B
C
几何语言
在Rt?ABC中
∠C=90°,∠A=30°
∴
BC=
AB
当堂训练
1.有一直角三角尺,30°角所对直角边长是6cm,则斜边的长是(
)
A
.3cm
B.
6
cmc
C.10
cm
D.
12
cm
2.如图,在等边三角形ABC中,AB=10cm,D是AB的中点,过点D作DE⊥AC于点E,则EC的长是(
)
A.
2.5
cm
B.
5
cm
C.7
cm
D.
7.5
cm
D
D
A
B
D
E
C
∟
3.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则BD的长是(
).
C
A
B
D
C
∟
4.如图,在Rt△ABC中,∠ACB=90°,∠B=15°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18cm,则AC的长是
.
9cm
A
B
D
C
∟
E
当堂训练
5.如图所示,点P是∠AOB平分线上的一点,过点P作PC∥OA交OB于点C,若∠AOB=30°,OC=4,求点P到OA的距离PD.
A
B
O
D
P
C
∟
E
解:过P作PE⊥OB,如图所示
∵PC∥OA∴∠PCB=∠AOB=30°
∠AOP=∠OPC,
∵OP是∠AOB平分线
∴∠AOP=∠POB,PD=PE,
∴∠POB=∠OPC,
∴CO=PC,
∵OC=4,∴PC=4
∵∠PCB=30°,PE⊥OB,
∴PE=
PC=2,∴PD=2
1
2
归纳总结
利用含30°角的直角三角形的性质解决问题的方法
解题时,一般是先寻找30°角所在的直角三角形,得到斜边与直角边的关系,当30°角不在一个直角三角形中时,可考虑作垂线得到含30°角的直角三角形,或作等腰三角形构造顶角的邻补角为60°.当三角形中含15°,30°,60°,120°角时,也可通过添加辅助线,构造含30°角的直角三角形求解.
达标检测
1.右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,
∠A=
30
°,
则BC=
m、DE=
m.
3.7
1.85
2.如图,一棵树在一次强台风中于离地面3m处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为(
)
A.6
m
B.9
m
C.12m
D.15m
B
30°
3.如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC,AB于点M,N,且BM=3,则CM=
.
6
A
B
M
C
∟
N
达标检测
4.如图所示是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h=_____
m
4
150°
A
B
M
C
D
达标检测
5.如图,已知∠MAN=120°,AC平分∠MAN,B,D分别在射线AN,AM上.
(1)若∠ABC=∠ADC=90°,如图1,求证:AD+AB=AC
A
B
D
N
M
C
∟
∟
图1
达标检测
(2)若∠ABC+∠ADC=180°,如图2,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由
A
B
图2
D
N
M
C
达标检测
课堂小结
直角三角形的性质
1.例2、变式2;
达标2、3;
提能5-8;
2.预习13.4最短路径;
作业布置
