人教版数学八年级上册14.1.2 幂的乘方课件(共30张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.1.2 幂的乘方课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 812.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览









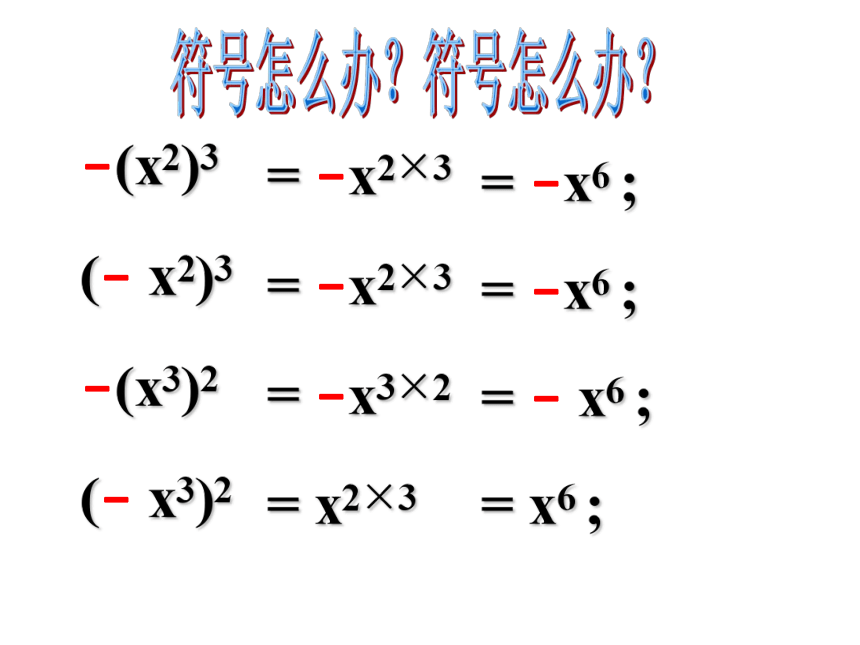
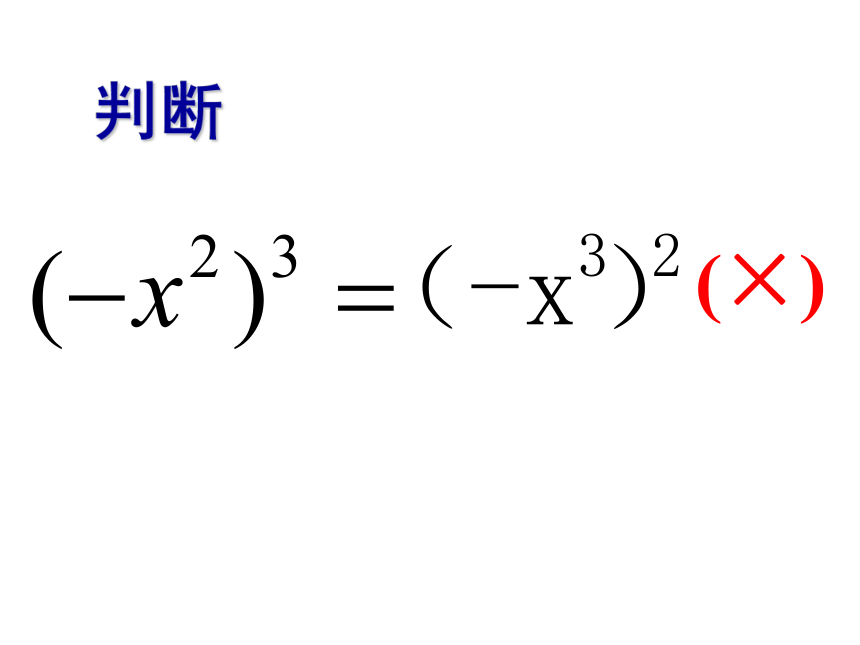
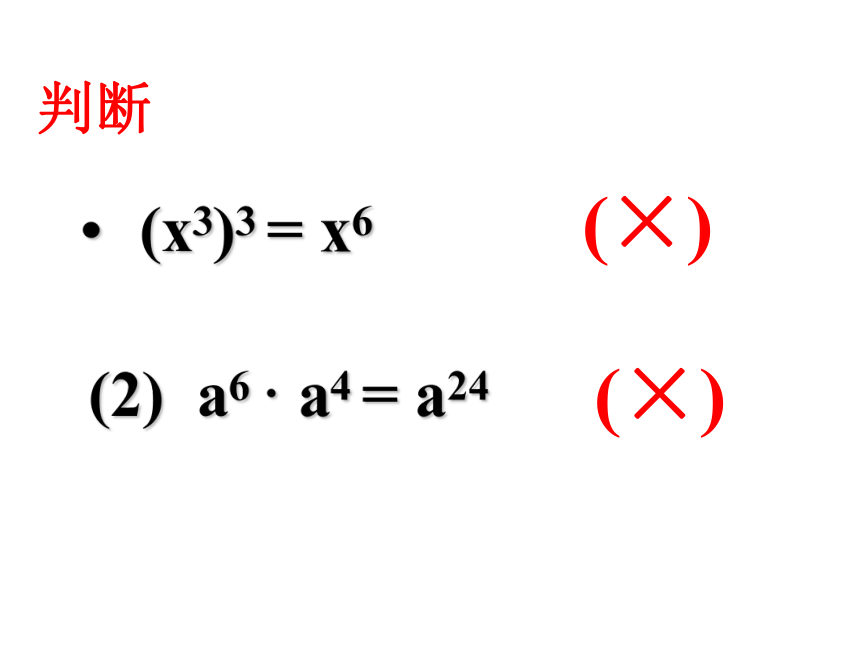
文档简介
(共30张PPT)
14.1.2
幂的乘方
同底数幂的乘法:
am
·
an
=
am+n
(m、n为正整数)
同底数幂相乘,底数不变,指数相加。
am
·
an
·
ap
=
am+n+p
(
m、n、p为正整数)
知识回顾
如果三个正方体的棱长分别为10?、104、a?,其体积分别为多少?
解:
从上面的计算中你发现了什么???
(104)3
=1012
=104×104×104
问题引导下再学习
猜想:
(am)n
=amn
(m,n都是正整数).
幂的乘方,
底数
,指数
。
不变
相乘
如
(23)4
=23×4
=212
幂的乘方公式
(1)
(103)5
(2)
(a4)4
(3)
(am)2
(4)
-(x4)3
跟踪练习
当堂训练幂的乘方法则(重点)
计算:
(1)(x2)3;
(3)(a3)2-(a2)3;
(2)-(x9)8;
(4)(a2)3·a5.
思路导引:运用幂的乘方法则,运算时要先确定符号.
幂的乘方的逆运算:
(1)x13·x7=x(
)=(
)5=(
)4=(
)10;
(2)a2m
=(
)2
=(
)m
(m为正整数).
20
x4
x5
x2
am
a2
探究二幂的乘方法则的逆用
1.(m2)3·m4等于(
)
B
A.m9
B.m10
C.m12
D.m14
2.计算:
(1)[(x+y)2]6=____________;
(2)a8+(a2)4=____________.
2a8
3.已知
x2n=3,则(xn)4=________.
9
点拔:(xn)4=x4n=(x2n)2=32=9.
(x+y)12
4.已知
10a=5,10b=6,则
102a+103b的值为________.
241
点拨:102a+103b=(10a)2+(10b)3=52+63=241.
跟踪训练
例题训练:已知
ax=3,ay=2,试求
a2x+3y
【规律总结】对于幂的乘方与同底数幂的乘法的混合运算,
先算乘方,再算同底数幂的乘法;幂的乘方与加减混合运算时,
先乘方,后加减,注意合并同类项.
的值.
-(x2)3
八年级
数学
=
-x2×3
=
-x6
;
符号怎么办?
(-
x2)3
=
-x2×3
=
-x6
;
-(x3)2
=
-x3×2
=
-
x6
;
(-
x3)2
=
x2×3
=
x6
;
判断
(×)
(×)
(×)
(2)
a6
·
a4
=
a24
(x3)3
=
x6
判断
运算
种类
公式
法则
中运算
计算结果
底数
指数
同底数幂乘法
幂的乘方
乘法
乘方
不变
不变
指数
相加
指数
相乘
幂的乘方和同底数幂的乘法的比较
达标检测
⑵(a-b)3[(a-b)3]2
⑶[(x-y)2]2[(y-x)2]3
1、
3.
已知3×9n=37,求:n的值.
2.
已知53n=25,求:n的值.
4、(1)已知2x+5y-3=0,求
4x
·
32y的值
(2)已知
2x
=a,
2y
=b,求
22x+3y
的值
(3)已知
22n+1
+
4n
=48,
求
n
的值
(4)比较375,2100的大小
(5)若(9n)2
=
38
,则n为______
小结:
今天,我们学到了什么?
幂的乘方的运算性质:
(am)n
=
amn
(
m,n
都是正整数
).
同底数幂乘法的运算性质:
am
·
an=
am+n
(
m,n
都是正整数
)
底数 ,指数 。
不变
相加
底数 ,指数 。
不变
相乘
问题引导下再学习
一般地,对于任意底数a,b与任意正整数n,我们都有
即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘
积的因式为三项或三项以上运算法则仍成立:
当堂训练
2.已知
xn=3,yn=2,求(xy)3n的值.
达标检测
3.已知,xm=
,xn=3.求下列各式的值:
(1)x
m+n;
(2)
x2m?x2n;
(3)
x
3m+2n.
解:
(1)
x
m+n=x
m?x
n=
×3=
;
(2)
x2m?x2n=(x
m
)2?(x
n)2=(
)2×32=
×
9
=
;
(3)
x
3m+2n=x3m?x2n=(x
m)3?(x
n)2=(
)3×32
=
×
9
=
小结
1.
积的乘方的法则:
用式子表示:(ab)n=__(n是正整数).
语言叙述:积的乘方,等于把积的每一个因式分别__,再把所得的幂__.
2.
运用积的乘方法则时要注意什么?
(1)每一个因式都要乘方,
(2)还有符号问题.
3.积的乘方法则的逆用:
anbn=
(n是正整数)
八年级
数学
练一练
多重乘方也具有这一性质
相信你准能做对哟
练习
计算:
(103)3;
(2)
(x3)2;
(3)
-
(
xm
)5
;
(4)
(a2
)3?
a5;
(5)
0.254?82;
(6)
8?86?0.255;
(7)
[(m-n)2]3+(m-n)3(n-m)3.
1.已知,44?83=2x,求x的值.
实践与创新
在255,344,433,522这四个幂中,
数值最大的一个是———。
解:255=25×11=(25)11=3211
344=34×11=(34)11=8111
433=43×11=(43)11=6411
522=52×11=(52)11=2511
所以数值最大的一个是______
344
拓展:
3
.
2
同类训练
方法指导
b>c>a
∵124>123>122,
a>b>c
14.1.2
幂的乘方
同底数幂的乘法:
am
·
an
=
am+n
(m、n为正整数)
同底数幂相乘,底数不变,指数相加。
am
·
an
·
ap
=
am+n+p
(
m、n、p为正整数)
知识回顾
如果三个正方体的棱长分别为10?、104、a?,其体积分别为多少?
解:
从上面的计算中你发现了什么???
(104)3
=1012
=104×104×104
问题引导下再学习
猜想:
(am)n
=amn
(m,n都是正整数).
幂的乘方,
底数
,指数
。
不变
相乘
如
(23)4
=23×4
=212
幂的乘方公式
(1)
(103)5
(2)
(a4)4
(3)
(am)2
(4)
-(x4)3
跟踪练习
当堂训练幂的乘方法则(重点)
计算:
(1)(x2)3;
(3)(a3)2-(a2)3;
(2)-(x9)8;
(4)(a2)3·a5.
思路导引:运用幂的乘方法则,运算时要先确定符号.
幂的乘方的逆运算:
(1)x13·x7=x(
)=(
)5=(
)4=(
)10;
(2)a2m
=(
)2
=(
)m
(m为正整数).
20
x4
x5
x2
am
a2
探究二幂的乘方法则的逆用
1.(m2)3·m4等于(
)
B
A.m9
B.m10
C.m12
D.m14
2.计算:
(1)[(x+y)2]6=____________;
(2)a8+(a2)4=____________.
2a8
3.已知
x2n=3,则(xn)4=________.
9
点拔:(xn)4=x4n=(x2n)2=32=9.
(x+y)12
4.已知
10a=5,10b=6,则
102a+103b的值为________.
241
点拨:102a+103b=(10a)2+(10b)3=52+63=241.
跟踪训练
例题训练:已知
ax=3,ay=2,试求
a2x+3y
【规律总结】对于幂的乘方与同底数幂的乘法的混合运算,
先算乘方,再算同底数幂的乘法;幂的乘方与加减混合运算时,
先乘方,后加减,注意合并同类项.
的值.
-(x2)3
八年级
数学
=
-x2×3
=
-x6
;
符号怎么办?
(-
x2)3
=
-x2×3
=
-x6
;
-(x3)2
=
-x3×2
=
-
x6
;
(-
x3)2
=
x2×3
=
x6
;
判断
(×)
(×)
(×)
(2)
a6
·
a4
=
a24
(x3)3
=
x6
判断
运算
种类
公式
法则
中运算
计算结果
底数
指数
同底数幂乘法
幂的乘方
乘法
乘方
不变
不变
指数
相加
指数
相乘
幂的乘方和同底数幂的乘法的比较
达标检测
⑵(a-b)3[(a-b)3]2
⑶[(x-y)2]2[(y-x)2]3
1、
3.
已知3×9n=37,求:n的值.
2.
已知53n=25,求:n的值.
4、(1)已知2x+5y-3=0,求
4x
·
32y的值
(2)已知
2x
=a,
2y
=b,求
22x+3y
的值
(3)已知
22n+1
+
4n
=48,
求
n
的值
(4)比较375,2100的大小
(5)若(9n)2
=
38
,则n为______
小结:
今天,我们学到了什么?
幂的乘方的运算性质:
(am)n
=
amn
(
m,n
都是正整数
).
同底数幂乘法的运算性质:
am
·
an=
am+n
(
m,n
都是正整数
)
底数 ,指数 。
不变
相加
底数 ,指数 。
不变
相乘
问题引导下再学习
一般地,对于任意底数a,b与任意正整数n,我们都有
即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘
积的因式为三项或三项以上运算法则仍成立:
当堂训练
2.已知
xn=3,yn=2,求(xy)3n的值.
达标检测
3.已知,xm=
,xn=3.求下列各式的值:
(1)x
m+n;
(2)
x2m?x2n;
(3)
x
3m+2n.
解:
(1)
x
m+n=x
m?x
n=
×3=
;
(2)
x2m?x2n=(x
m
)2?(x
n)2=(
)2×32=
×
9
=
;
(3)
x
3m+2n=x3m?x2n=(x
m)3?(x
n)2=(
)3×32
=
×
9
=
小结
1.
积的乘方的法则:
用式子表示:(ab)n=__(n是正整数).
语言叙述:积的乘方,等于把积的每一个因式分别__,再把所得的幂__.
2.
运用积的乘方法则时要注意什么?
(1)每一个因式都要乘方,
(2)还有符号问题.
3.积的乘方法则的逆用:
anbn=
(n是正整数)
八年级
数学
练一练
多重乘方也具有这一性质
相信你准能做对哟
练习
计算:
(103)3;
(2)
(x3)2;
(3)
-
(
xm
)5
;
(4)
(a2
)3?
a5;
(5)
0.254?82;
(6)
8?86?0.255;
(7)
[(m-n)2]3+(m-n)3(n-m)3.
1.已知,44?83=2x,求x的值.
实践与创新
在255,344,433,522这四个幂中,
数值最大的一个是———。
解:255=25×11=(25)11=3211
344=34×11=(34)11=8111
433=43×11=(43)11=6411
522=52×11=(52)11=2511
所以数值最大的一个是______
344
拓展:
3
.
2
同类训练
方法指导
b>c>a
∵124>123>122,
a>b>c
