人教版数学八年级上册14.2.1平方差公式课件(共27张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.2.1平方差公式课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 23:47:50 | ||
图片预览








文档简介
(共27张PPT)
问题引入
某学校对操场进行改造,原来操场是长方形,改建后为正方形,设正方形的边长为a米,正方形的边长比原来长方形的长少b米,比原来长方形的宽多b米,问操场的面积比原来大了还是小了?前后相差了多少平方米?
14.2.1
平方差公式
1.掌握平方差公式的结构特征,能运用公式进行计算。
学习目标
重点:平方差公式的探究及应用.
难点:灵活运用平方差公式进行计算.
问题引导下再学习
复习备用
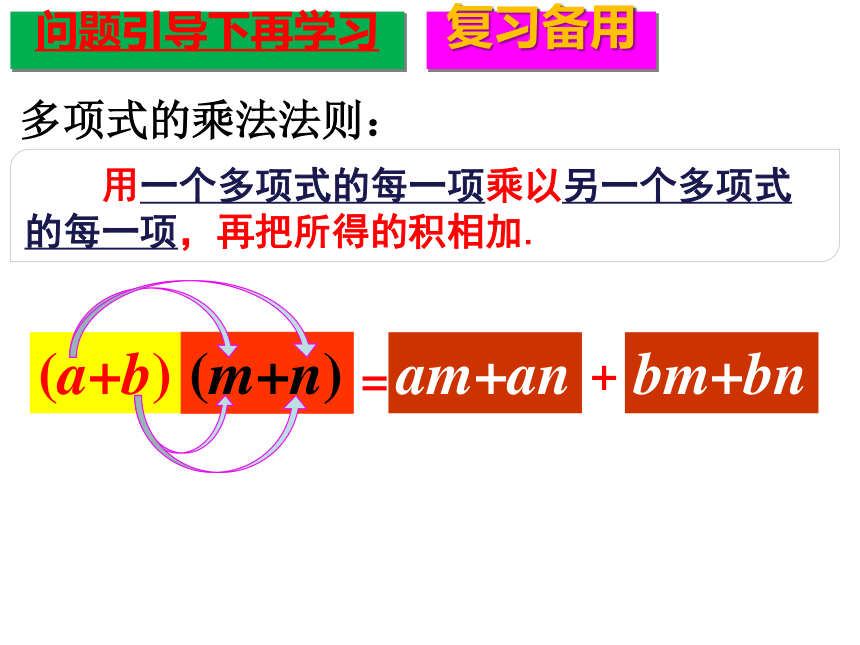
多项式的乘法法则:
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
am+an
bm+bn
+
=
(m+n)
(a+b)
知识点一:平方差公式
探究:计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x﹣1)=
;
(2)(m+2)(m﹣2)=
;
(3)(2x+1)(2x﹣1)=
.
x2-1
4x
2-1
m2-4
这几个运算都是形如a+b的多项式与形如a
-b的多项式相乘.
(a+b)(a-b)=a2-ab+ab-b2
=a2-b2
新知归纳
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积等于这两个数的平方差.
平方差公式:
知识点一:平方差公式
注:这里的两数可以是两个数字,也可以是两个整式等等.
新知归纳
(a+b)(a-b)
=
a
2
-
b
2
平方差公式:
知识点一:平方差公式
平方差公式变式:
(b+a)(-b+a)=a2-b2
(-a+b)(-a-b)=(-a)2-b2
相同为a
相同项2-相反项2
相反为b
合理加括号
(
)
(
)
当堂训练
(1)(2+a)(a?2)
(2)(?4k+3)(?4k?3)
(3)(1?x)(?x?1)
(4)(?x?1)(x+1)
(5)(x+3)(x?2)
(6)(a+b+c)(a+b?c)
可以
可以
可以
不可以
不可以
可以
a2?22
(-4k)2?32
(-x)2?12
(a+b)2?c2
1、下列式子可以用平方差公式计算吗?
当堂训练:即时3
归纳总结
变化形式
应用举例
平方差公式的变化及应用
(4)指数变化
(a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4
(1)位置变化
(b+a)(-b+a)=(a+b)(a-b)=a2-b2
(2)符号变化
(-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
(3)系数变化
(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2
(6)连用公式变化
(a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4
(5)增项变化
(a-b+c)(a-b-c)=(a-b)2-c2
当堂训练
例1:用平方差公式计算
(1)
(3x+2)(3x-2)
;
(2)
(b+2a)(2a﹣b);
(3)
(-x+2y)(-x-2y).
找符号相同项与符号相反项,相同为a
,相反为b,结果为:相同项2-相反项2
题型一:计算
注意
?
1、先把要计算的式子与公式对照,
2、哪个是
a
哪个是
b
(1)平方差公式中的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式.
(2)在运用公式时,要分清哪个相当于公式中的a,哪个相当于公式中的b,不要混淆.
归纳总结
当堂训练:例1
当堂训练
当堂训练
题型二:简便计算
当堂训练:
当堂训练:变式3
观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,7×9=82-1,…把发现的规律用含字母n(n为正整数)的等式表示为
.
(2n-1)(2n+1)=4n2-1
当堂训练
题型三:规律问题
当堂训练:提能7
解:原式=(100+99)(100-99)+
(98+97)(98-97)+…+(2+1)(2-1)
=100+99+98+97+…+2+1
=5050
计算:
1002
–992
+982
-972+
…
+22
-12
3、计算:
当堂训练:提能9
当堂训练:提能9
例、(c-a+b)(b-c+a),
是否可用平方差公式计算?
怎样应用公式计算?
练习、将下列各式变形为可利用平方差公式计算的形式:
(1)(a+2b+3)(a+2b-3)
(2)(a+2b-3)(a-2b+3)
(3)(a-2b+3)(a-2b-3)
(4)(a-2b-3)(a+2b-3)
(5)(3a-5b-2c)(-3a-5b+2c)
(6)(x-y+m-n)(x+y-m-n)
达标检测
1.计算(1-m)(-m-1),结果正确的是(
)
A.m2-2m-1
B.m2-1
C.1-m
D.m2-2m+1
2.三个连续整数,中间的一个是n,则这三个整数的积是(
)
A
.3n
B.n3
C.n3-1
D.n3-n
3.若x+y=6,x-y=5,则x2-y2的值是
.
4.若计算(x+m)(x+
)的结果不含字母x的一次项,则(x+m)(x-m)=
.
B
D
30
达标检测
5.化简(x+y+z)2ー(x+yー2)2的结果是(
)
A.
4yz
B
.8xy
C
.4yz+4xz
D
.8xz
6.阅读理解:引人新数i,新数i满足分配律、结合律交换律.已知i2=-1,那么(1+2i)?(1-2i)=
.
7.如果(2a+2b-3)(2a+2b+3)=40,那么a+b=
.
8.已知xーy=2,yーz=2,z+x=2,则x2-z2的值是
.
9.1003×997=
.
C
5
±3.5
8
999991
问题引入
某学校对操场进行改造,原来操场是长方形,改建后为正方形,设正方形的边长为a米,正方形的边长比原来长方形的长少b米,比原来长方形的宽多b米,问操场的面积比原来大了还是小了?前后相差了多少平方米?
14.2.1
平方差公式
1.掌握平方差公式的结构特征,能运用公式进行计算。
学习目标
重点:平方差公式的探究及应用.
难点:灵活运用平方差公式进行计算.
问题引导下再学习
复习备用
多项式的乘法法则:
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
am+an
bm+bn
+
=
(m+n)
(a+b)
知识点一:平方差公式
探究:计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x﹣1)=
;
(2)(m+2)(m﹣2)=
;
(3)(2x+1)(2x﹣1)=
.
x2-1
4x
2-1
m2-4
这几个运算都是形如a+b的多项式与形如a
-b的多项式相乘.
(a+b)(a-b)=a2-ab+ab-b2
=a2-b2
新知归纳
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积等于这两个数的平方差.
平方差公式:
知识点一:平方差公式
注:这里的两数可以是两个数字,也可以是两个整式等等.
新知归纳
(a+b)(a-b)
=
a
2
-
b
2
平方差公式:
知识点一:平方差公式
平方差公式变式:
(b+a)(-b+a)=a2-b2
(-a+b)(-a-b)=(-a)2-b2
相同为a
相同项2-相反项2
相反为b
合理加括号
(
)
(
)
当堂训练
(1)(2+a)(a?2)
(2)(?4k+3)(?4k?3)
(3)(1?x)(?x?1)
(4)(?x?1)(x+1)
(5)(x+3)(x?2)
(6)(a+b+c)(a+b?c)
可以
可以
可以
不可以
不可以
可以
a2?22
(-4k)2?32
(-x)2?12
(a+b)2?c2
1、下列式子可以用平方差公式计算吗?
当堂训练:即时3
归纳总结
变化形式
应用举例
平方差公式的变化及应用
(4)指数变化
(a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4
(1)位置变化
(b+a)(-b+a)=(a+b)(a-b)=a2-b2
(2)符号变化
(-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
(3)系数变化
(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2
(6)连用公式变化
(a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4
(5)增项变化
(a-b+c)(a-b-c)=(a-b)2-c2
当堂训练
例1:用平方差公式计算
(1)
(3x+2)(3x-2)
;
(2)
(b+2a)(2a﹣b);
(3)
(-x+2y)(-x-2y).
找符号相同项与符号相反项,相同为a
,相反为b,结果为:相同项2-相反项2
题型一:计算
注意
?
1、先把要计算的式子与公式对照,
2、哪个是
a
哪个是
b
(1)平方差公式中的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式.
(2)在运用公式时,要分清哪个相当于公式中的a,哪个相当于公式中的b,不要混淆.
归纳总结
当堂训练:例1
当堂训练
当堂训练
题型二:简便计算
当堂训练:
当堂训练:变式3
观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,7×9=82-1,…把发现的规律用含字母n(n为正整数)的等式表示为
.
(2n-1)(2n+1)=4n2-1
当堂训练
题型三:规律问题
当堂训练:提能7
解:原式=(100+99)(100-99)+
(98+97)(98-97)+…+(2+1)(2-1)
=100+99+98+97+…+2+1
=5050
计算:
1002
–992
+982
-972+
…
+22
-12
3、计算:
当堂训练:提能9
当堂训练:提能9
例、(c-a+b)(b-c+a),
是否可用平方差公式计算?
怎样应用公式计算?
练习、将下列各式变形为可利用平方差公式计算的形式:
(1)(a+2b+3)(a+2b-3)
(2)(a+2b-3)(a-2b+3)
(3)(a-2b+3)(a-2b-3)
(4)(a-2b-3)(a+2b-3)
(5)(3a-5b-2c)(-3a-5b+2c)
(6)(x-y+m-n)(x+y-m-n)
达标检测
1.计算(1-m)(-m-1),结果正确的是(
)
A.m2-2m-1
B.m2-1
C.1-m
D.m2-2m+1
2.三个连续整数,中间的一个是n,则这三个整数的积是(
)
A
.3n
B.n3
C.n3-1
D.n3-n
3.若x+y=6,x-y=5,则x2-y2的值是
.
4.若计算(x+m)(x+
)的结果不含字母x的一次项,则(x+m)(x-m)=
.
B
D
30
达标检测
5.化简(x+y+z)2ー(x+yー2)2的结果是(
)
A.
4yz
B
.8xy
C
.4yz+4xz
D
.8xz
6.阅读理解:引人新数i,新数i满足分配律、结合律交换律.已知i2=-1,那么(1+2i)?(1-2i)=
.
7.如果(2a+2b-3)(2a+2b+3)=40,那么a+b=
.
8.已知xーy=2,yーz=2,z+x=2,则x2-z2的值是
.
9.1003×997=
.
C
5
±3.5
8
999991
