人教版七年级数学上册 1.2.1 有理数 课件 (共25张PPT)
文档属性
| 名称 | 人教版七年级数学上册 1.2.1 有理数 课件 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
1.2.1
有理数
第一章
有理数
人教版七年级数学上册
通过前面的学习,我们已经知道很多不同类型的
数,现在请同学们任意说出你认为是不同类型的几个
数.
新课导入
问题1:同学们在数学课上学习了很多种不同类型的数,你能举几个例子吗?
我们学过的数有:
正整数,如1,2,3,.
.
.;
零,0;
负整数,如-1,-2,-3,.
.
.;
正分数,如
.
.
.;
负分数,如
.
.
.;
所有正整数组成正整数集合,所有负整数组成负整数集合
这里的小数可以化出分数,我们也把它们看成分数
合作探究
问题2:观察下列这些数,能否将所写的数按如下类型进行归类呢?
正整数
负整数
负分数
负分数
合作探究
正整数
0
负整数
整数
正分数
负分数
分数
有理数
从小学开始,我们首先认识正整数,后来又增加了0和正分数,在认识了负整数和负分数后,对数的认识就扩充到有理数范围.
归纳总结
1.
定义:整数和分数统称有理数.
(1)
一个有理数不是整数就是分数.
(2)
如果一个数既不是整数也不是分数,那么它一定
不是有理数.
2.
整数和分数:正整数、0、负整数统称整数.正分数、
负分数统称分数.
归纳总结
3.
几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数.
归纳总结
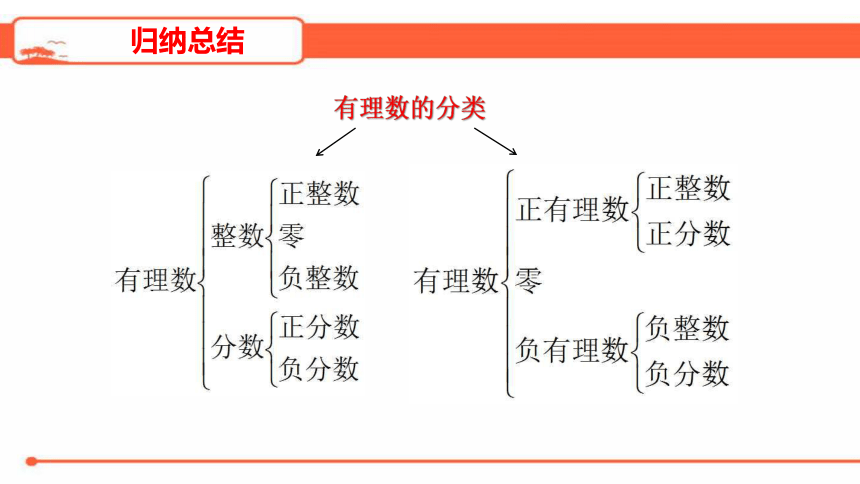
问题3:你能对有理数进行分类吗?
方法1:按定义分类.
方法2:按性质符号分类:
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
归纳总结
有理数的分类
归纳总结
例1
把下列各数填入相应的集合圈里:
.
.
.
正数集合
.
.
.
负数集合
.
.
.
整数集合
.
.
.
分数集合
变式练习:同桌之间,一名同学说出几个有理数,另一名同学指出每个数属于哪一类?
例题精析
定义:把满足一定条件的所有数放在一起,就组成一类
数的集合.
(1)
一类数的集合必须是符合条件的所有数,不能遗漏.
(2)
若一类数的集合有无数个数,则表示这个数的集合
时,除写上题中给定的有限个数之外,必须加上省
略号.
归纳总结
例2
〈易错题〉在-3.5,
,0,
,0.161
616…
中,有理数共有( )
A.5个 B.4个 C.3个 D.2个
导引:判断有理数要紧扣其定义,也就是看这个数是
否是整数或分数.
例题精析
整数和分数统称为有理数.对于分数的识别有两个
误区:(1)不是所有的小数都能化成分数,如无限不循
环的小数就不能化成分数;(2)有些数形似分数,但不
是分数,例如本题中
归纳总结
例3
下列说法正确的有几个?
①零是整数;
②零是有理数;
③零是自然数;
④零是正数;
⑤零是负数;
⑥零是非负数.
例4
下列说法错误的有几个?
①负整数和负分数统称为负有理数;
②正整数,0和负整数统称为整数;
③正有理数与负有理数组成全体有理数;
④存在最小的有理数;
⑤存在最小的正整数;
⑥存在最小的正数
例题精析
例5
〈易错题〉把下列各数分别填入相应的集合里:
-2,0,-0.314,25%,11,
非负有理数集合:{ ,…};
整数集合:{ ,…};
自然数集合:{ ,…};
分数集合:{
,…};
非正整数集合:{ ,…}.
导引:要严格按照各类数的概念进行填写,非负有理数包
含正有理数和0;非正整数包含负整数和0.
例题精析
(1)非负有理数一定是有理数,它包含正有理数和0,
不要误认为是除负有理数以外的任何数;
(2)非正整数一定是整数;
(3)找各类数时,要时刻考虑它是否包括“0”.
归纳总结
2.
不属于( )
A.负数
B.分数
C.负分数
D.整数
1. 在数
0,2,-3,-1.2
中,属于负整数的是
( )
A.0
B.2
C.-3
D.-1.2
3.
下列说法不正确的是( )
A.-0.5不是分数
B.0是整数
C.
不是整数
D.-2既是负数又是整数
C
D
A
课堂精练
4.
下列说法错误的是( )
A.负整数和负分数统称为负有理数
B.正整数、负整数和0统称为整数
C.正有理数和负有理数统称为有理数
D.0是整数,但不是分数
C
课堂精练
5.
给出一个有理数-107.987及下列判断:
(1)这个数不是分数,但是有理数;
(2)这个数是负数,也是分数;
(3)这个数与π一样,不是有理数;
(4)这个数是一个负小数,也是负分数.
其中判断正确的个数是( )
A.1
B.2
C.3
D.4
B
课堂精练
6.
将下列各数填入下图所示的相应的圈内.
-1,0,2,
正数集合
整数集合
负数集合
导引:圈中的公共部分的意义:各个集合的公共部分;题中2
是正数,也是整数;-3,-1既是整数,又是负数.
课堂精练
将数填入带有交叉部分的集合中,先填交叉的部
分,如:正数和整数的交叉部分,先填正整数,然后
在正数集合中填除正整数外的正数,即正分数.
课堂精练
7.
下列选项中,所填的数正确的是( )
A.正数集合:
B.非负数集合:
C.分数集合:
D.整数集合:
8.
所有的正整数和负整数合在一起构成( )
A.整数集合
B.有理数集合
C.自然数集合
D.以上说法都不对
A
D
课堂精练
请同学们回顾本节课所学知识,回答下列问题:
1.有理数是怎样定义的?
2.有理数有几种分类方法?具体是怎样分类的?
3.有理数的学习过程中,应注意什么?
课堂小结
有理数有两种常用的分类方式.
课堂小结
有理数的分类:对有理数分类时,要注意分类标准,做到不重复、不遗漏;若按集合分类,则每个集合
最后要加上“…”.
有理数的判别技巧:
(1)凡是整数、分数,都是有理数.
(2)有限小数和无限循环小数都可化为分数,所以是有理
数;无限不循环小数不能化为分数,所以不是有理数.
课堂小结
1.2.1
有理数
第一章
有理数
人教版七年级数学上册
通过前面的学习,我们已经知道很多不同类型的
数,现在请同学们任意说出你认为是不同类型的几个
数.
新课导入
问题1:同学们在数学课上学习了很多种不同类型的数,你能举几个例子吗?
我们学过的数有:
正整数,如1,2,3,.
.
.;
零,0;
负整数,如-1,-2,-3,.
.
.;
正分数,如
.
.
.;
负分数,如
.
.
.;
所有正整数组成正整数集合,所有负整数组成负整数集合
这里的小数可以化出分数,我们也把它们看成分数
合作探究
问题2:观察下列这些数,能否将所写的数按如下类型进行归类呢?
正整数
负整数
负分数
负分数
合作探究
正整数
0
负整数
整数
正分数
负分数
分数
有理数
从小学开始,我们首先认识正整数,后来又增加了0和正分数,在认识了负整数和负分数后,对数的认识就扩充到有理数范围.
归纳总结
1.
定义:整数和分数统称有理数.
(1)
一个有理数不是整数就是分数.
(2)
如果一个数既不是整数也不是分数,那么它一定
不是有理数.
2.
整数和分数:正整数、0、负整数统称整数.正分数、
负分数统称分数.
归纳总结
3.
几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数.
归纳总结
问题3:你能对有理数进行分类吗?
方法1:按定义分类.
方法2:按性质符号分类:
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
归纳总结
有理数的分类
归纳总结
例1
把下列各数填入相应的集合圈里:
.
.
.
正数集合
.
.
.
负数集合
.
.
.
整数集合
.
.
.
分数集合
变式练习:同桌之间,一名同学说出几个有理数,另一名同学指出每个数属于哪一类?
例题精析
定义:把满足一定条件的所有数放在一起,就组成一类
数的集合.
(1)
一类数的集合必须是符合条件的所有数,不能遗漏.
(2)
若一类数的集合有无数个数,则表示这个数的集合
时,除写上题中给定的有限个数之外,必须加上省
略号.
归纳总结
例2
〈易错题〉在-3.5,
,0,
,0.161
616…
中,有理数共有( )
A.5个 B.4个 C.3个 D.2个
导引:判断有理数要紧扣其定义,也就是看这个数是
否是整数或分数.
例题精析
整数和分数统称为有理数.对于分数的识别有两个
误区:(1)不是所有的小数都能化成分数,如无限不循
环的小数就不能化成分数;(2)有些数形似分数,但不
是分数,例如本题中
归纳总结
例3
下列说法正确的有几个?
①零是整数;
②零是有理数;
③零是自然数;
④零是正数;
⑤零是负数;
⑥零是非负数.
例4
下列说法错误的有几个?
①负整数和负分数统称为负有理数;
②正整数,0和负整数统称为整数;
③正有理数与负有理数组成全体有理数;
④存在最小的有理数;
⑤存在最小的正整数;
⑥存在最小的正数
例题精析
例5
〈易错题〉把下列各数分别填入相应的集合里:
-2,0,-0.314,25%,11,
非负有理数集合:{ ,…};
整数集合:{ ,…};
自然数集合:{ ,…};
分数集合:{
,…};
非正整数集合:{ ,…}.
导引:要严格按照各类数的概念进行填写,非负有理数包
含正有理数和0;非正整数包含负整数和0.
例题精析
(1)非负有理数一定是有理数,它包含正有理数和0,
不要误认为是除负有理数以外的任何数;
(2)非正整数一定是整数;
(3)找各类数时,要时刻考虑它是否包括“0”.
归纳总结
2.
不属于( )
A.负数
B.分数
C.负分数
D.整数
1. 在数
0,2,-3,-1.2
中,属于负整数的是
( )
A.0
B.2
C.-3
D.-1.2
3.
下列说法不正确的是( )
A.-0.5不是分数
B.0是整数
C.
不是整数
D.-2既是负数又是整数
C
D
A
课堂精练
4.
下列说法错误的是( )
A.负整数和负分数统称为负有理数
B.正整数、负整数和0统称为整数
C.正有理数和负有理数统称为有理数
D.0是整数,但不是分数
C
课堂精练
5.
给出一个有理数-107.987及下列判断:
(1)这个数不是分数,但是有理数;
(2)这个数是负数,也是分数;
(3)这个数与π一样,不是有理数;
(4)这个数是一个负小数,也是负分数.
其中判断正确的个数是( )
A.1
B.2
C.3
D.4
B
课堂精练
6.
将下列各数填入下图所示的相应的圈内.
-1,0,2,
正数集合
整数集合
负数集合
导引:圈中的公共部分的意义:各个集合的公共部分;题中2
是正数,也是整数;-3,-1既是整数,又是负数.
课堂精练
将数填入带有交叉部分的集合中,先填交叉的部
分,如:正数和整数的交叉部分,先填正整数,然后
在正数集合中填除正整数外的正数,即正分数.
课堂精练
7.
下列选项中,所填的数正确的是( )
A.正数集合:
B.非负数集合:
C.分数集合:
D.整数集合:
8.
所有的正整数和负整数合在一起构成( )
A.整数集合
B.有理数集合
C.自然数集合
D.以上说法都不对
A
D
课堂精练
请同学们回顾本节课所学知识,回答下列问题:
1.有理数是怎样定义的?
2.有理数有几种分类方法?具体是怎样分类的?
3.有理数的学习过程中,应注意什么?
课堂小结
有理数有两种常用的分类方式.
课堂小结
有理数的分类:对有理数分类时,要注意分类标准,做到不重复、不遗漏;若按集合分类,则每个集合
最后要加上“…”.
有理数的判别技巧:
(1)凡是整数、分数,都是有理数.
(2)有限小数和无限循环小数都可化为分数,所以是有理
数;无限不循环小数不能化为分数,所以不是有理数.
课堂小结
