人教版七年级数学上册1.2.2 数轴 教学课件(共27张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.2.2 数轴 教学课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 841.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
1.2.2
数轴
第一章
有理数
人教版七年级数学上册
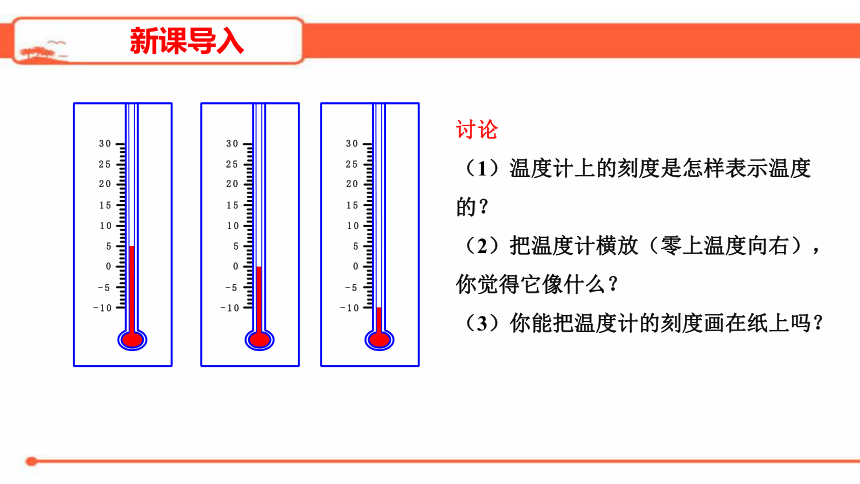
新课导入
讨论
(1)温度计上的刻度是怎样表示温度的?
(2)把温度计横放(零上温度向右),你觉得它像什么?
(3)你能把温度计的刻度画在纸上吗?
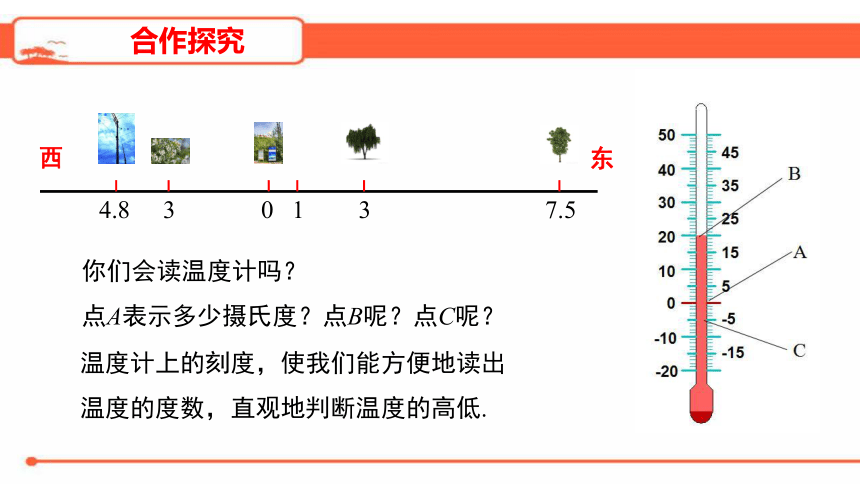
问题1:在一条东西向的马路上,有一个汽车站牌,汽车站牌往东3
m和7.5
m处分别有一棵柳树和一棵杨树,汽车站牌往西3
m和4.8
m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
提问:(1)马路可以用什么几何图形代表?
(2)你认为站牌起什么作用?
合作探究
(3)你是怎么确定问题中各物体的位置的?
问题:如何用数表示这些树、电线杆与汽车站牌的相对位置呢?
合作探究
0
1
3
7.5
3
4.8
东
西
你们会读温度计吗?
点A表示多少摄氏度?点B呢?点C呢?
温度计上的刻度,使我们能方便地读出温度的度数,直观地判断温度的高低.
合作探究
请同学们根据以下提示简单介绍一下温度计:
(1)温度计刻度的正负是怎样规定的?
以什么为基准?基准刻度线表示多少摄氏度?
(2)每摄氏度两条刻度线之间的距离有什么特点?
合作探究
现在我们将温度计水平放置,是否给我们以直线的形象.
既然温度计上的刻度,使我们能够方便地读出温度的度数,那么我们能否尝试着仿照温度计的模式,设计一条特殊的直线,从而用这条直线上的点表示所学的数呢?
合作探究
问题:
(1)画数轴的步骤是什么?
(2)根据上述实例的经验,“原点”起什么作用?
(3)你是怎么理解“选取适当的长度为单位长度”的?
(4)数轴上,在原点的右边,离原点越远的点所表示的数
;在原点的左边,离原点越远的点所表示的数
.
合作探究
如何画数轴?
1.首先画一条水平直线;
2.在直线上任意取一点表示0,我们把这点称为原点.
3.把这条直线上从原点向右的方向规定为正方向,画箭头表示,向左方向规定为负方向.
4.最后根据需要选取适当的长度作为单位长度,在直线上,从原点向右每隔一个单位长度取一点,依次表示1,2,3,…从原点向左每隔一个单位长度取一点,依次表示-1,-2,-3,…与温度计一样,两条刻度线之间的距离要相等.单位长度要统一.
这样的直线我们把它称为数轴.
合作探究
思考:谁能根据我们刚才所画的数轴,说说数轴包含哪些方面?
数轴的三要素
原点
正方向
单位长度
那什么是数轴呢?
数轴:像这样规定了原点、正方向和单位长度的直线叫做数轴.
合作探究
①观察数轴上的有理数位于数轴左(下)边的数总比右(上)
的数小.
②一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数a的点在原点的____边,与原点的距离是____个单位长度.
合作探究
(1)数轴是一条直线
数轴的特征
(2)数轴三要素
原点
正方向
单位长度
归纳总结
问题:
(1)画数轴的步骤是什么?
(2)根据上述实例的经验,“原点”起什么作用?
(3)你是怎么理解“选取适当的长度为单位长度”的?
(4)数轴上,在原点的右边,离原点越远的点所表示的数__________;在原点的左边,离原点越远的点所表示的数_____________.
合作探究
数轴的画法:
一画:画一条直线(一般是水平直线);
二取:选取原点,并用这点表示数字0;
三定:确定正方向,用箭头表示(一般规定向右为正);
四统一:单位长度应统一;
五标数:在原点左右两边依次标上对应的刻度数.
归纳总结
例1
下列图形中哪些是数轴,哪些不是,为什么?
A
1
C
0
-1
2
3
B
1
0
2
-1
D
0
-2
1
2
识别数轴,要紧扣数轴的定义,围绕数轴的“三要素”进行判断,三者缺一不可.
例题精析
例1
如图,写出数轴上点A,B,C,D,E表示的数.
例题精析
例2
如何把一个有理数用数轴上的点来表示?
在数轴上画出表示下列各数的点:
思考:有理数都可以用数轴上的一个点来表示吗?
例题精析
(1)
画数轴关键就是在一条直线上画出数轴的“三要素”;
(2)
数轴被原点分成两个区域:
①从原点向右表示正数区域,标数时从左至右;
②从原点向左表示负数区域,标数时从右至左;
(3)
数标注在直线刻度下方.
归纳总结
例3
在数轴上,表示数-2,2.6,
,
0,
,-1的点中,在原点左边的点有
个.
例4
在数轴上点A表示-4,如果把原点O向负方向移动1.5个单位,那么在新数轴上点A表示的数是(
)
A.
B.
C.
D.
例题精析
例5
如图,数轴上有三点A,B,C.
请回答:
(1)三点A,B,C中,任意两点之间的距离是多少个单位长度?
(2)将点C沿数轴向左移动8个单位长度,此时点A,B,C
中任意两点之间的距离是多少个单位长度?
例题精析
在数轴上求两个点之间的距离,只需要数一数两
个点之间相隔多少个单位长度即可.注意:距离不可
能是负数.
归纳总结
1 下列各图中,所画数轴正确的是( )
D
2 下列说法中,错误的是( )
A.在数轴上,原点位置的确定是任意的
B.在数轴上,正方向可以是从原点向右,也可以是
从原点向左
C.在数轴上,确定单位长度时可根据需要任意选取
D.数轴是规定了原点、正方向、单位长度的直线
B
课堂精练
3
如图,分别用数轴上的点A,B,C,D表示数,正确的是( )
A.点D表示-2.5 B.点C表示-1.25
C.点B表示1.5
D.点A表示1.25
C
4
在数轴上表示-2,0,6.3,
的点中,在原点右边的点
有( )
A.0个 B.1个 C.2个 D.3个
C
课堂精练
5
a,b,c在数轴上的位置如图所示,下列说法正确的是( )
A.a,b,c都表示正数
B.a,b,c都表示负数
C.a,b表示正数,c表示负数
D.a,b表示负数,c表示正数
C
6
在数轴上表示数-1和2
019的两点分别为A和B,则A,B两点之间的距离为( )
A.2
018
B.2
019
C.2
020
D.2
021
C
课堂精练
7
如图,已知数轴上的点A,B,C,D分别表示数-2,1,2,3,则表示3-
的点P应落在线段
( )
A.AD上
B.OB上
C.BC上
D.CD上
B
课堂精练
1.数轴定义包含三层含义:
(1)数轴是一条直线;
(2)数轴有“三要素”:原点、正方向、单位长度;
(3)“规定”是指原点位置、正方向选取、单位长度大小都根据需要而定.
课堂小结
2.数轴的“两点应用”:(1)根据有理数在数轴上找到表示该有理数的点;(2)根据数轴上表示有理数的点读出其表示的有理数,简单地说,一是知数画点,二是知点读数.
3.数轴上的点与有理数间的关系:所有的有理数都可用数轴上的点来表示,但数轴上的点表示的不一定都是有理数.
课堂小结
1.2.2
数轴
第一章
有理数
人教版七年级数学上册
新课导入
讨论
(1)温度计上的刻度是怎样表示温度的?
(2)把温度计横放(零上温度向右),你觉得它像什么?
(3)你能把温度计的刻度画在纸上吗?
问题1:在一条东西向的马路上,有一个汽车站牌,汽车站牌往东3
m和7.5
m处分别有一棵柳树和一棵杨树,汽车站牌往西3
m和4.8
m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
提问:(1)马路可以用什么几何图形代表?
(2)你认为站牌起什么作用?
合作探究
(3)你是怎么确定问题中各物体的位置的?
问题:如何用数表示这些树、电线杆与汽车站牌的相对位置呢?
合作探究
0
1
3
7.5
3
4.8
东
西
你们会读温度计吗?
点A表示多少摄氏度?点B呢?点C呢?
温度计上的刻度,使我们能方便地读出温度的度数,直观地判断温度的高低.
合作探究
请同学们根据以下提示简单介绍一下温度计:
(1)温度计刻度的正负是怎样规定的?
以什么为基准?基准刻度线表示多少摄氏度?
(2)每摄氏度两条刻度线之间的距离有什么特点?
合作探究
现在我们将温度计水平放置,是否给我们以直线的形象.
既然温度计上的刻度,使我们能够方便地读出温度的度数,那么我们能否尝试着仿照温度计的模式,设计一条特殊的直线,从而用这条直线上的点表示所学的数呢?
合作探究
问题:
(1)画数轴的步骤是什么?
(2)根据上述实例的经验,“原点”起什么作用?
(3)你是怎么理解“选取适当的长度为单位长度”的?
(4)数轴上,在原点的右边,离原点越远的点所表示的数
;在原点的左边,离原点越远的点所表示的数
.
合作探究
如何画数轴?
1.首先画一条水平直线;
2.在直线上任意取一点表示0,我们把这点称为原点.
3.把这条直线上从原点向右的方向规定为正方向,画箭头表示,向左方向规定为负方向.
4.最后根据需要选取适当的长度作为单位长度,在直线上,从原点向右每隔一个单位长度取一点,依次表示1,2,3,…从原点向左每隔一个单位长度取一点,依次表示-1,-2,-3,…与温度计一样,两条刻度线之间的距离要相等.单位长度要统一.
这样的直线我们把它称为数轴.
合作探究
思考:谁能根据我们刚才所画的数轴,说说数轴包含哪些方面?
数轴的三要素
原点
正方向
单位长度
那什么是数轴呢?
数轴:像这样规定了原点、正方向和单位长度的直线叫做数轴.
合作探究
①观察数轴上的有理数位于数轴左(下)边的数总比右(上)
的数小.
②一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数a的点在原点的____边,与原点的距离是____个单位长度.
合作探究
(1)数轴是一条直线
数轴的特征
(2)数轴三要素
原点
正方向
单位长度
归纳总结
问题:
(1)画数轴的步骤是什么?
(2)根据上述实例的经验,“原点”起什么作用?
(3)你是怎么理解“选取适当的长度为单位长度”的?
(4)数轴上,在原点的右边,离原点越远的点所表示的数__________;在原点的左边,离原点越远的点所表示的数_____________.
合作探究
数轴的画法:
一画:画一条直线(一般是水平直线);
二取:选取原点,并用这点表示数字0;
三定:确定正方向,用箭头表示(一般规定向右为正);
四统一:单位长度应统一;
五标数:在原点左右两边依次标上对应的刻度数.
归纳总结
例1
下列图形中哪些是数轴,哪些不是,为什么?
A
1
C
0
-1
2
3
B
1
0
2
-1
D
0
-2
1
2
识别数轴,要紧扣数轴的定义,围绕数轴的“三要素”进行判断,三者缺一不可.
例题精析
例1
如图,写出数轴上点A,B,C,D,E表示的数.
例题精析
例2
如何把一个有理数用数轴上的点来表示?
在数轴上画出表示下列各数的点:
思考:有理数都可以用数轴上的一个点来表示吗?
例题精析
(1)
画数轴关键就是在一条直线上画出数轴的“三要素”;
(2)
数轴被原点分成两个区域:
①从原点向右表示正数区域,标数时从左至右;
②从原点向左表示负数区域,标数时从右至左;
(3)
数标注在直线刻度下方.
归纳总结
例3
在数轴上,表示数-2,2.6,
,
0,
,-1的点中,在原点左边的点有
个.
例4
在数轴上点A表示-4,如果把原点O向负方向移动1.5个单位,那么在新数轴上点A表示的数是(
)
A.
B.
C.
D.
例题精析
例5
如图,数轴上有三点A,B,C.
请回答:
(1)三点A,B,C中,任意两点之间的距离是多少个单位长度?
(2)将点C沿数轴向左移动8个单位长度,此时点A,B,C
中任意两点之间的距离是多少个单位长度?
例题精析
在数轴上求两个点之间的距离,只需要数一数两
个点之间相隔多少个单位长度即可.注意:距离不可
能是负数.
归纳总结
1 下列各图中,所画数轴正确的是( )
D
2 下列说法中,错误的是( )
A.在数轴上,原点位置的确定是任意的
B.在数轴上,正方向可以是从原点向右,也可以是
从原点向左
C.在数轴上,确定单位长度时可根据需要任意选取
D.数轴是规定了原点、正方向、单位长度的直线
B
课堂精练
3
如图,分别用数轴上的点A,B,C,D表示数,正确的是( )
A.点D表示-2.5 B.点C表示-1.25
C.点B表示1.5
D.点A表示1.25
C
4
在数轴上表示-2,0,6.3,
的点中,在原点右边的点
有( )
A.0个 B.1个 C.2个 D.3个
C
课堂精练
5
a,b,c在数轴上的位置如图所示,下列说法正确的是( )
A.a,b,c都表示正数
B.a,b,c都表示负数
C.a,b表示正数,c表示负数
D.a,b表示负数,c表示正数
C
6
在数轴上表示数-1和2
019的两点分别为A和B,则A,B两点之间的距离为( )
A.2
018
B.2
019
C.2
020
D.2
021
C
课堂精练
7
如图,已知数轴上的点A,B,C,D分别表示数-2,1,2,3,则表示3-
的点P应落在线段
( )
A.AD上
B.OB上
C.BC上
D.CD上
B
课堂精练
1.数轴定义包含三层含义:
(1)数轴是一条直线;
(2)数轴有“三要素”:原点、正方向、单位长度;
(3)“规定”是指原点位置、正方向选取、单位长度大小都根据需要而定.
课堂小结
2.数轴的“两点应用”:(1)根据有理数在数轴上找到表示该有理数的点;(2)根据数轴上表示有理数的点读出其表示的有理数,简单地说,一是知数画点,二是知点读数.
3.数轴上的点与有理数间的关系:所有的有理数都可用数轴上的点来表示,但数轴上的点表示的不一定都是有理数.
课堂小结
