人教版七年级数学上册 1.2.3 相反数 教学课件(27张PPT)
文档属性
| 名称 | 人教版七年级数学上册 1.2.3 相反数 教学课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
1.2.3
相反数
第一章
有理数
人教版七年级数学上册
活动:看图讲故事.
新课导入
探究
在数轴上,与原点的距离是2的点有几个?这些点各
表示哪个数?
设a是一个正数.
数轴上与原点的距离等于a的点有几
个?这些点表示的数有什么关系?
合作探究
两位同学A、B背靠背,一人向右走2步,一人向左走2步
.
一人向右走5步,一人向左走5步
.
请问:如果向右为正,向左为负,
向右走2步,向左走2步各记作什么?
向右走5步,向左走5步各记作什么?
向右走2步记作
;向左走2步记作
,
向右走5步记作
;向左走5步记作
.
+2
-2
+5
-5
合作探究
大家来观察一下这个数轴,请问:
数轴上与原点的距离是2的点有 个,
它们分别是 和
.
数轴上与原点的距离是5的点有 个,
它们分别是 和
.
2
2
-2
2
5
-5
合作探究
探究问题:观察下列数,并把它们在数轴上标出:
6和-6,
和
,7和-7,
和
.
(1)上述各对数之间有什么特点?
(2)表示每对数的两个点在数轴上有什么特点?
(3)你能够写出具有上述特点的数么?
合作探究
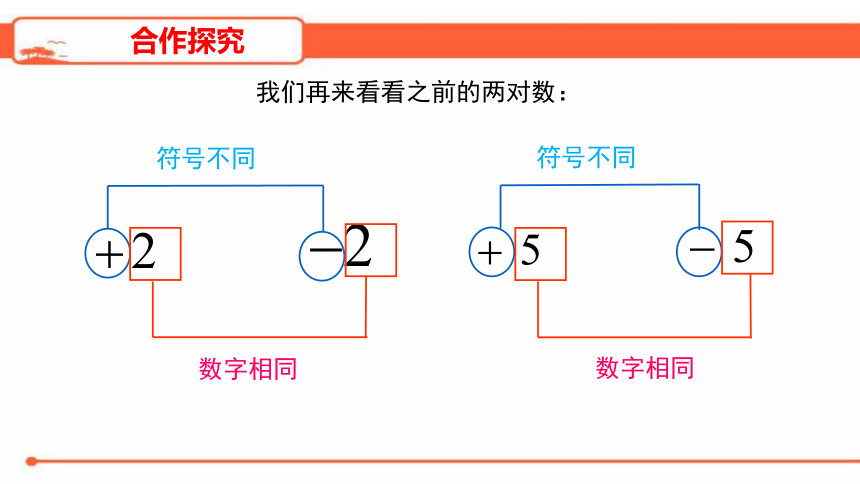
我们再来看看之前的两对数:
符号不同
数字相同
符号不同
数字相同
合作探究
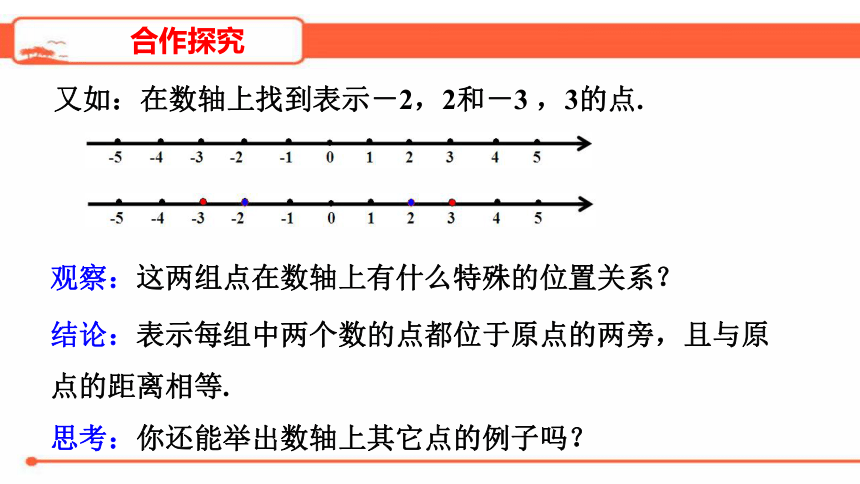
又如:在数轴上找到表示-2,2和-3
,3的点.
观察:这两组点在数轴上有什么特殊的位置关系?
结论:表示每组中两个数的点都位于原点的两旁,且与原点的距离相等.
思考:你还能举出数轴上其它点的例子吗?
合作探究
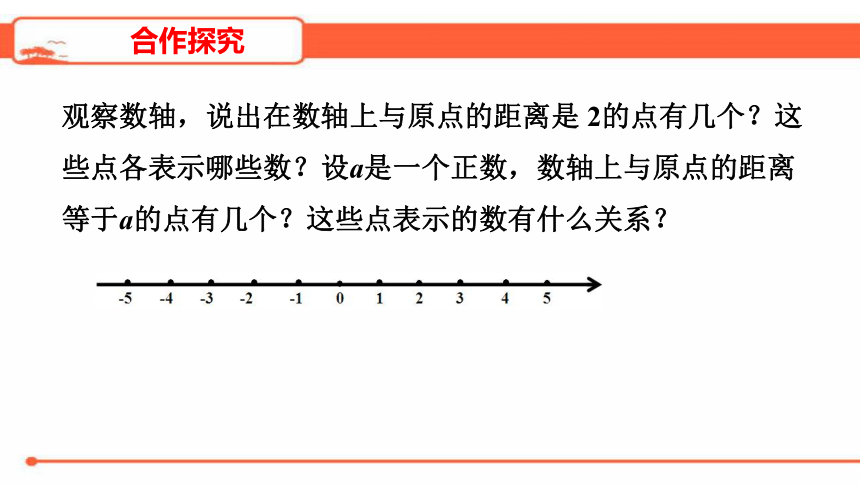
观察数轴,说出在数轴上与原点的距离是
2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
合作探究
数轴上与原点的距离是
2的点有两个,表示为-
2和2;如果a是一个正数,数轴上与原点的距离是a的
点有两个,它们分别在原点左右,表示为-a和a,我
们说这两个点关于原点对称.
归纳总结
定义:像-2和2,-5和5这样,只有符号不同的两个数称互为相反数.
例如:3的相反数是-3,;-3的相反数是3;
-1.5的相反数是1.5;1.5是-1.5的相反数.
相反数的几何意义:互为相反数的两个数分布在原点两侧且到原点的距离相等.位于原点两边且到原点的距离相等的两个点所表示的数是相反数.
规定:0的相反数是0.
什么叫相反数?
归纳总结
相反数的代数意义:只有符号不同的两个数叫做
互为相反数.特殊规定:0的相反数是0.
2.
相反数的求法:求一个数的相反数就是在这个数
的前面加上“-”号,即a的相反数是-a,其实
质是改变这个数的符号.
归纳总结
例1
抢
答
1.2.5的相反数是
____
2.8.2和____是相反数
3.0的相反数是
_____
4.______是-100的相反数
5.-1.1是______
的相反数
6.______的相反数是-5
例题精析
例2
判断
1.-5是相反数
(
)
2.符号不同的两个数是相反数(
)
3.互为相反数的两个数一定不相等(
)
4.任何一个正数的相反数都是负数(
)
5.一个数的相反数的相反数等于这个数(
)
例题精析
例3
已知有理数m,-3,n在数轴上的位置如图所示,请将m,-3,n的相反数在数轴上表示出来,并将这六个数用“<”连接起来.
互为相反数的两个数分布在原点两侧且到原点的距离相等
例题精析
例4
下列说法正确的是( )
A.-2是相反数
B.
与-2互为相反数
C.-3与+2互为相反数
D.
与0.5互为相反数
导引:判断两个数是否互为相反数,按其定义从两个
方面去看:符号(+、-)和所含数字(相同).
例题精析
(1)相反数不能单独存在,前提是“互为”;
(2)判断两个数是否互为相反数,要从两个方面看,
一是符号不能相同;
二是数字一定要相同.
归纳总结
例5
分别写出下列各数的相反数.
-3,2,4.5,0,-
.
导引:根据相反数的代数意义(只有符号不同的两个数
互为相反数),直接写出一个数的相反数.
例题精析
(1)在一个省略正号的正数的前面添加负号,即可
得到这个数的相反数;
(2)直接去掉负数的负号即可得到它的相反数,0的相反数是0,任何有理数有且只有一个相反数.
归纳总结
例6
化简下列各数:
(1)-[+(-1)];(2)-{[-…(-1)
…]}.
导引:(1)-[+(-1)]表示+(-1)的相反数,即-1的相反数;
(2)2n-1为奇数,所以结果为负数.
(2n-1)个负号,n为正整数
例题精析
从上面的学习中你发现了什么?
观察归纳:
在一个数前面加上“-”号,表示它的相反数;
在一个数前面加上“+”号,表示它的本身.
一般的,数a和-a互为相反数,特别的,0的相反数是0
.
例如:+3的相反数是-(+3)=-3,数a的相反数是-a.
归纳总结
(共n个负号)
在一个数的前面加“+”或“-”,结果的符号与前面“-”的个数有关:
①若有奇数个“-”,则最后结果为“-”;
②若有偶数个“-”,则最后结果为“+”;
③它与“+”的个数无关
.
归纳总结
1
-15的相反数是( )
A.15 B.-15 C.±15 D.
2
一个数的相反数是3,这个数是( )
A.
B.-
C.3
D.-3
A
D
3
在2,-2,6,8这四个数中,互为相反数
的是( )
A.-2与2
B.2与8
C.-2与6
D.6与8
A
课堂精练
4 如图,表示互为相反数的两个数的点是________.
B
C
5 判断下列说法是否正确:
(1)-3是相反数
;
(2)+3是相反数;
(3)3是-3的相反数;
(4)-3与+3互为相反数.
×
×
√
√
课堂精练
7
化简下列各数:
-(-68)
,-(+0.75),
,
-(+3.8)
68,-0.75,
,-3.8
6
如果a=-
a,那么表示a
的点在数轴上的什么位置?
原点
8
a的相反数是-(+5),则a=________.
5
课堂精练
9
化简下列各数:
(1)-[-(+2)]=______;
(2)-[-(-2
017)]=________;
(3)-[+(-18)]=__________;
(4)
___________.
2
-2017
18
10 下列说法:①m与-m互为相反数,因此它们一定不相等;②相反数等于它本身的数只有0;③正数和负数互为相反数;④负数的相反数是正数;⑤a的相反数一定是负数.其中正确的个数是( )
A.1
B.2
C.3
D.4
B
课堂精练
1.相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a的相反
数是-a,特殊地:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个点
所表示的数互为相反数.
2.多重符号化简的方法规律:
方法一:把所有的正号去掉;负号的个数是偶数个时结果为正,是奇数个时结果为负,即“奇负偶正”.
方法二:采用两个同号得正,异号得负,分层化简.
课堂小结
1.2.3
相反数
第一章
有理数
人教版七年级数学上册
活动:看图讲故事.
新课导入
探究
在数轴上,与原点的距离是2的点有几个?这些点各
表示哪个数?
设a是一个正数.
数轴上与原点的距离等于a的点有几
个?这些点表示的数有什么关系?
合作探究
两位同学A、B背靠背,一人向右走2步,一人向左走2步
.
一人向右走5步,一人向左走5步
.
请问:如果向右为正,向左为负,
向右走2步,向左走2步各记作什么?
向右走5步,向左走5步各记作什么?
向右走2步记作
;向左走2步记作
,
向右走5步记作
;向左走5步记作
.
+2
-2
+5
-5
合作探究
大家来观察一下这个数轴,请问:
数轴上与原点的距离是2的点有 个,
它们分别是 和
.
数轴上与原点的距离是5的点有 个,
它们分别是 和
.
2
2
-2
2
5
-5
合作探究
探究问题:观察下列数,并把它们在数轴上标出:
6和-6,
和
,7和-7,
和
.
(1)上述各对数之间有什么特点?
(2)表示每对数的两个点在数轴上有什么特点?
(3)你能够写出具有上述特点的数么?
合作探究
我们再来看看之前的两对数:
符号不同
数字相同
符号不同
数字相同
合作探究
又如:在数轴上找到表示-2,2和-3
,3的点.
观察:这两组点在数轴上有什么特殊的位置关系?
结论:表示每组中两个数的点都位于原点的两旁,且与原点的距离相等.
思考:你还能举出数轴上其它点的例子吗?
合作探究
观察数轴,说出在数轴上与原点的距离是
2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
合作探究
数轴上与原点的距离是
2的点有两个,表示为-
2和2;如果a是一个正数,数轴上与原点的距离是a的
点有两个,它们分别在原点左右,表示为-a和a,我
们说这两个点关于原点对称.
归纳总结
定义:像-2和2,-5和5这样,只有符号不同的两个数称互为相反数.
例如:3的相反数是-3,;-3的相反数是3;
-1.5的相反数是1.5;1.5是-1.5的相反数.
相反数的几何意义:互为相反数的两个数分布在原点两侧且到原点的距离相等.位于原点两边且到原点的距离相等的两个点所表示的数是相反数.
规定:0的相反数是0.
什么叫相反数?
归纳总结
相反数的代数意义:只有符号不同的两个数叫做
互为相反数.特殊规定:0的相反数是0.
2.
相反数的求法:求一个数的相反数就是在这个数
的前面加上“-”号,即a的相反数是-a,其实
质是改变这个数的符号.
归纳总结
例1
抢
答
1.2.5的相反数是
____
2.8.2和____是相反数
3.0的相反数是
_____
4.______是-100的相反数
5.-1.1是______
的相反数
6.______的相反数是-5
例题精析
例2
判断
1.-5是相反数
(
)
2.符号不同的两个数是相反数(
)
3.互为相反数的两个数一定不相等(
)
4.任何一个正数的相反数都是负数(
)
5.一个数的相反数的相反数等于这个数(
)
例题精析
例3
已知有理数m,-3,n在数轴上的位置如图所示,请将m,-3,n的相反数在数轴上表示出来,并将这六个数用“<”连接起来.
互为相反数的两个数分布在原点两侧且到原点的距离相等
例题精析
例4
下列说法正确的是( )
A.-2是相反数
B.
与-2互为相反数
C.-3与+2互为相反数
D.
与0.5互为相反数
导引:判断两个数是否互为相反数,按其定义从两个
方面去看:符号(+、-)和所含数字(相同).
例题精析
(1)相反数不能单独存在,前提是“互为”;
(2)判断两个数是否互为相反数,要从两个方面看,
一是符号不能相同;
二是数字一定要相同.
归纳总结
例5
分别写出下列各数的相反数.
-3,2,4.5,0,-
.
导引:根据相反数的代数意义(只有符号不同的两个数
互为相反数),直接写出一个数的相反数.
例题精析
(1)在一个省略正号的正数的前面添加负号,即可
得到这个数的相反数;
(2)直接去掉负数的负号即可得到它的相反数,0的相反数是0,任何有理数有且只有一个相反数.
归纳总结
例6
化简下列各数:
(1)-[+(-1)];(2)-{[-…(-1)
…]}.
导引:(1)-[+(-1)]表示+(-1)的相反数,即-1的相反数;
(2)2n-1为奇数,所以结果为负数.
(2n-1)个负号,n为正整数
例题精析
从上面的学习中你发现了什么?
观察归纳:
在一个数前面加上“-”号,表示它的相反数;
在一个数前面加上“+”号,表示它的本身.
一般的,数a和-a互为相反数,特别的,0的相反数是0
.
例如:+3的相反数是-(+3)=-3,数a的相反数是-a.
归纳总结
(共n个负号)
在一个数的前面加“+”或“-”,结果的符号与前面“-”的个数有关:
①若有奇数个“-”,则最后结果为“-”;
②若有偶数个“-”,则最后结果为“+”;
③它与“+”的个数无关
.
归纳总结
1
-15的相反数是( )
A.15 B.-15 C.±15 D.
2
一个数的相反数是3,这个数是( )
A.
B.-
C.3
D.-3
A
D
3
在2,-2,6,8这四个数中,互为相反数
的是( )
A.-2与2
B.2与8
C.-2与6
D.6与8
A
课堂精练
4 如图,表示互为相反数的两个数的点是________.
B
C
5 判断下列说法是否正确:
(1)-3是相反数
;
(2)+3是相反数;
(3)3是-3的相反数;
(4)-3与+3互为相反数.
×
×
√
√
课堂精练
7
化简下列各数:
-(-68)
,-(+0.75),
,
-(+3.8)
68,-0.75,
,-3.8
6
如果a=-
a,那么表示a
的点在数轴上的什么位置?
原点
8
a的相反数是-(+5),则a=________.
5
课堂精练
9
化简下列各数:
(1)-[-(+2)]=______;
(2)-[-(-2
017)]=________;
(3)-[+(-18)]=__________;
(4)
___________.
2
-2017
18
10 下列说法:①m与-m互为相反数,因此它们一定不相等;②相反数等于它本身的数只有0;③正数和负数互为相反数;④负数的相反数是正数;⑤a的相反数一定是负数.其中正确的个数是( )
A.1
B.2
C.3
D.4
B
课堂精练
1.相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a的相反
数是-a,特殊地:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个点
所表示的数互为相反数.
2.多重符号化简的方法规律:
方法一:把所有的正号去掉;负号的个数是偶数个时结果为正,是奇数个时结果为负,即“奇负偶正”.
方法二:采用两个同号得正,异号得负,分层化简.
课堂小结
