1.2 一定是直角三角形吗课件(共24张PPT)
文档属性
| 名称 | 1.2 一定是直角三角形吗课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 22:33:45 | ||
图片预览





文档简介
(共24张PPT)
数学北师大版
八年级
1.2
一定是直角三角形吗
在一个直角三角形中,两直角边的平方和等于斜边的平方.反过来,如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形吗?
分别以5,12,13;3,
4,
5;8,15,17;7,24,25为三边长作三角形,用量角器量一量,它们都是直角三角形吗?
每个三角形都满足较小两边长的平方和等于第三边长的平方.
做一做:
勾股定理逆定理:如果三角形的三边长a,b,c
满足a2+b2=c2
,那么这个三角形是直角三角形.
区别:勾股定理是直角三角形的性质定理,其逆定理是直角三角形的判定定理.
变式:
c2-b2
=a2
c2-a2
=b2
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
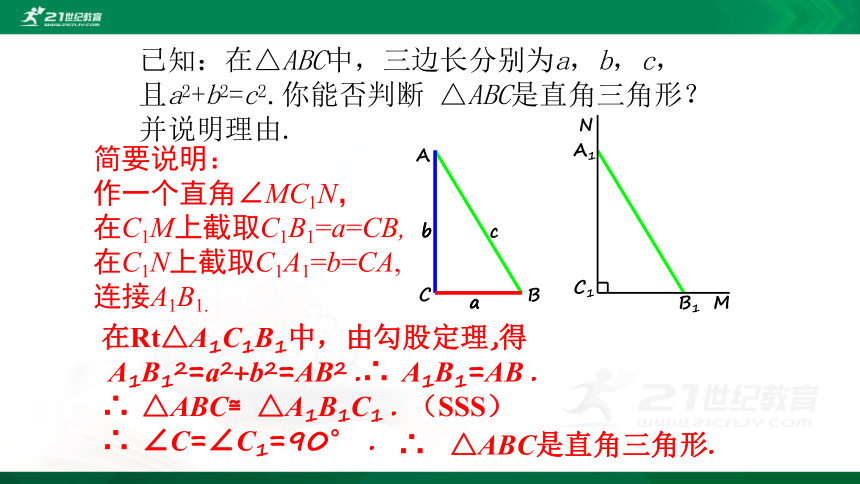
已知:在△ABC中,三边长分别为a,b,c,
且a2+b2=c2.你能否判断
△ABC是直角三角形?
并说明理由.
简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.
在Rt△A1C1B1中,由勾股定理,得
A1B12=a2+b2=AB2
.∴
A1B1=AB
.
∴
△ABC≌△A1B1C1
.
(SSS)
∴
∠C=∠C1=90°
.
∴
△ABC是直角三角形.
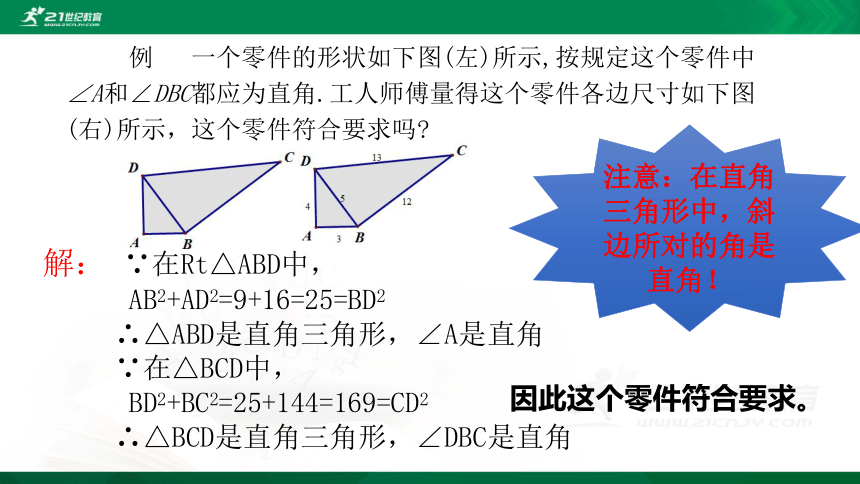
例
一个零件的形状如下图(左)所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如下图(右)所示,这个零件符合要求吗?
注意:在直角三角形中,斜边所对的角是直角!
解:
∵在Rt△ABD中,
AB2+AD2=9+16=25=BD2
∴△ABD是直角三角形,∠A是直角
∵在△BCD中,
BD2+BC2=25+144=169=CD2
∴△BCD是直角三角形,∠DBC是直角
因此这个零件符合要求。
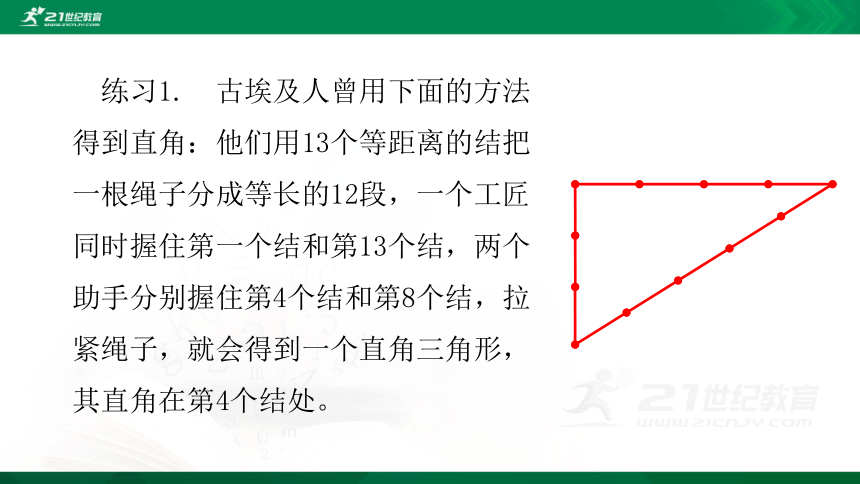
练习1.
古埃及人曾用下面的方法得到直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
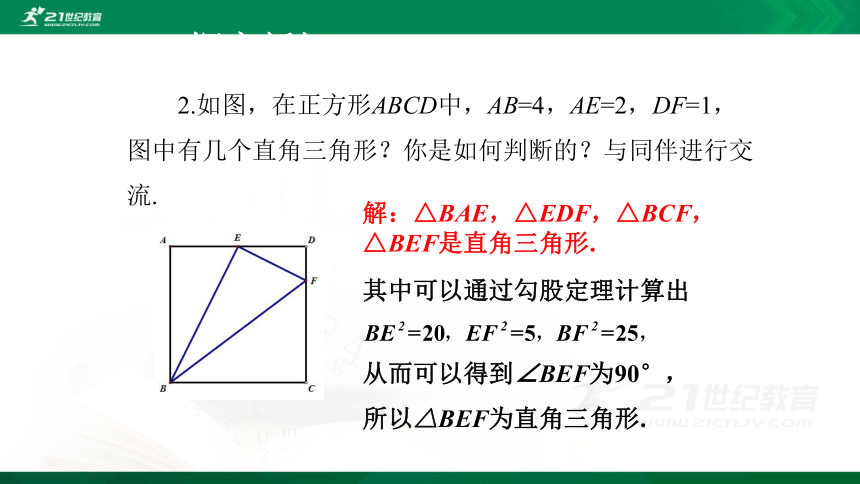
2.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形?你是如何判断的?与同伴进行交流.
探究新知
解:△BAE,△EDF,△BCF,△BEF是直角三角形.
其中可以通过勾股定理计算出
从而可以得到∠BEF为90°,
所以△BEF为直角三角形.
常用的勾股数:必是正整数
3,
4,
5
5,
12,
13
7,
24,
25
8,
15,
17
9,
40,
41
11,
60,
61
10,
24,
26
12,
35,
37
20,
21,
29
它们的K倍也成立,如3K,4K.5K还是勾股数.
(3k)2+(4k)2=25k2
=(5k)2
判断下列哪组数是勾股数:
(1)6,7,8;
(2)8,15,6;
(3)a=n2-1,b=2n,c=n2+1
(n>1)
(4)a=m2-n2,b=2mn,c=m2+n2
(m>n>0)
例2
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD
的面积。
解:连结BD,在Rt△ABD中,由勾股定理得BD=5cm
又∵在三角形BDC中,三边分别是5,12,13,满足勾股定理,
∴三角形BDC是直角三角形。
因此,四边形ABCD的面积为36平方厘米。
S四边形=SΔABD+SΔBDC=
解:(1)S△ABC=4×4-12×1×2-12×4×3-12×2×4=16-1-6-4=5.
所以△ABC的面积为5.
(2)△ABC是直角三角形.
理由如下.
因为小方格的边长为1,所以AB2=12+22=5,
AC2=22+42=20,BC2=32+42=25.所以B2+AC2=5+20=25=BC2.所以.
【例3】如图所示网格中的△ABC,若小方格的边长为1,请你根据所学的知识,解答下列问题:
(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
AB2+AC2=5+20=25=BC2.所以△ABC为直角三角形
课堂练习:1.
如图1-2-3,△ABC中,AD⊥BC,垂足为点D.
如果AD=6,BD=9,CD=4,那么∠BAC是直角吗?说明理由.
解:∠BAC是直角.理由如下.
因为AD⊥BC,所以∠ADB=∠ADC=90°.
因为AD=6,BD=9,CD=4,
所以AB2=AD2+BD2=117,AC2=AD2+CD2=52.
因为BC=BD+CD=13,
所以AB2+AC2=BC2=169.
所以∠BAC=90°.
2.
如图1-2-6,∠ABC为直角,BC长为3,AB长为4,AF长为12,正方形的面积为169,求△AFC的面积.
解:因为∠ABC为直角,BC长为3,AB长为4,
所以AC2=AB2+BC2=16+9=25.
因为正方形的面积为169,
所以FC2=169.
因为AF2+AC2=144+25=169=FC2,
所以△AFC为直角三角形.
所以∠FAC为直角.
所以S△AFC=0.5AF·AC=0.5×12×5=30.
3.已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,则下列条件:①a=4,b=
?,c=
?;②a2∶b2∶c2=1∶3∶2;③∠A
∶∠B∶∠C=3∶4∶5;④∠A=2∠B=2∠C.其中能判断△ABC是直角三角形的有?( )
A.1个 ????B.2个 ????C.3个 ????D.4个
答案????C ①∵a2+b2=?=
?,c2=
?=?,
∴此三角形是直角三角形;
②∵a2∶b2∶c2=1∶3∶2,∴a2+c2=b2,∴此三角形是直角三角形;
③∵∠A∶∠B∶∠C=3∶4∶5,∴设∠A=3x,则∠B=4x,
∠C=5x,∵∠A+∠B+∠C=180°,∴3x+4x+5x=180°,
解得x=15°,∴∠A=45°,∠B=60°,∠C=75°,
∴此三角形不是直角三角形;
④∵∠A=2∠B=2∠C,∴设∠B=∠C=x,则∠A=2x,∴x+x+
2x=180°,解得x=45°,∴∠A=2x=90°,
∴此三角形是直角三角形.故选C.
∴a2+b2=c2,
作业布置;
习题1.3
1,2,3,4
选讲内容
1.如图,点E是正方形ABCD内的一点,连接AE、BE、CE,△ABE≌△CBE'.若AE=1,BE=2,CE=3,则∠BE'C= ????度.
解析 连接EE',?
∵△ABE≌△CBE',
∴AE=CE',BE=BE',∠ABE=∠CBE',
∴∠EBE'是直角,∴△EBE'是直角三角形,∠BEE'=∠BE'E=45°,
∵AE=1,BE=2,∴BE'=2,E'C=1.
∵EE'2=22+22=8,CE'=1,EC=3,∴EC2=E′C2+EE'2,
∴△EE'C是直角三角形,∴∠EE'C=90°,
∴∠BE'C=135°.
2.在△ABC中,∠A,∠B,∠C的对边分别为a
,b,c,且满足c十a=2b,c-a=0.5b,则△ABC是什么特殊三角形?
解:∵c+a=2b,c-a=
0.5b,
∴(c+a)(c-a)=b2
即a2+b2=c2,
∴c2-a2=b2
∴△ABC是直角三角形,∠C=
90°
3.如图1
-2-8,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
解:(1)AP=CQ.证明如下:
∵△ABC为等边三角形,
∴AB=BC,∠ABC=60°.
又∵∠PBQ=60°,BQ
=
BP,
∴∠ABP=∠CBQ,△BPQ为等边三角形
∴△ABP≌△CBQ
∴AP=
CQ.
(2)若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
(2)△PQC为直角三角形.理由如下:
由(1)得AP=CQ,PQ=PB,
则CQ:
PQ:
PC=3:4:5
从而CQ2
+PQ2
=PC2,
∴∠PQC=90
∴△PQC为直角三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
八年级
1.2
一定是直角三角形吗
在一个直角三角形中,两直角边的平方和等于斜边的平方.反过来,如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形吗?
分别以5,12,13;3,
4,
5;8,15,17;7,24,25为三边长作三角形,用量角器量一量,它们都是直角三角形吗?
每个三角形都满足较小两边长的平方和等于第三边长的平方.
做一做:
勾股定理逆定理:如果三角形的三边长a,b,c
满足a2+b2=c2
,那么这个三角形是直角三角形.
区别:勾股定理是直角三角形的性质定理,其逆定理是直角三角形的判定定理.
变式:
c2-b2
=a2
c2-a2
=b2
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
已知:在△ABC中,三边长分别为a,b,c,
且a2+b2=c2.你能否判断
△ABC是直角三角形?
并说明理由.
简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.
在Rt△A1C1B1中,由勾股定理,得
A1B12=a2+b2=AB2
.∴
A1B1=AB
.
∴
△ABC≌△A1B1C1
.
(SSS)
∴
∠C=∠C1=90°
.
∴
△ABC是直角三角形.
例
一个零件的形状如下图(左)所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如下图(右)所示,这个零件符合要求吗?
注意:在直角三角形中,斜边所对的角是直角!
解:
∵在Rt△ABD中,
AB2+AD2=9+16=25=BD2
∴△ABD是直角三角形,∠A是直角
∵在△BCD中,
BD2+BC2=25+144=169=CD2
∴△BCD是直角三角形,∠DBC是直角
因此这个零件符合要求。
练习1.
古埃及人曾用下面的方法得到直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
2.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形?你是如何判断的?与同伴进行交流.
探究新知
解:△BAE,△EDF,△BCF,△BEF是直角三角形.
其中可以通过勾股定理计算出
从而可以得到∠BEF为90°,
所以△BEF为直角三角形.
常用的勾股数:必是正整数
3,
4,
5
5,
12,
13
7,
24,
25
8,
15,
17
9,
40,
41
11,
60,
61
10,
24,
26
12,
35,
37
20,
21,
29
它们的K倍也成立,如3K,4K.5K还是勾股数.
(3k)2+(4k)2=25k2
=(5k)2
判断下列哪组数是勾股数:
(1)6,7,8;
(2)8,15,6;
(3)a=n2-1,b=2n,c=n2+1
(n>1)
(4)a=m2-n2,b=2mn,c=m2+n2
(m>n>0)
例2
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD
的面积。
解:连结BD,在Rt△ABD中,由勾股定理得BD=5cm
又∵在三角形BDC中,三边分别是5,12,13,满足勾股定理,
∴三角形BDC是直角三角形。
因此,四边形ABCD的面积为36平方厘米。
S四边形=SΔABD+SΔBDC=
解:(1)S△ABC=4×4-12×1×2-12×4×3-12×2×4=16-1-6-4=5.
所以△ABC的面积为5.
(2)△ABC是直角三角形.
理由如下.
因为小方格的边长为1,所以AB2=12+22=5,
AC2=22+42=20,BC2=32+42=25.所以B2+AC2=5+20=25=BC2.所以.
【例3】如图所示网格中的△ABC,若小方格的边长为1,请你根据所学的知识,解答下列问题:
(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
AB2+AC2=5+20=25=BC2.所以△ABC为直角三角形
课堂练习:1.
如图1-2-3,△ABC中,AD⊥BC,垂足为点D.
如果AD=6,BD=9,CD=4,那么∠BAC是直角吗?说明理由.
解:∠BAC是直角.理由如下.
因为AD⊥BC,所以∠ADB=∠ADC=90°.
因为AD=6,BD=9,CD=4,
所以AB2=AD2+BD2=117,AC2=AD2+CD2=52.
因为BC=BD+CD=13,
所以AB2+AC2=BC2=169.
所以∠BAC=90°.
2.
如图1-2-6,∠ABC为直角,BC长为3,AB长为4,AF长为12,正方形的面积为169,求△AFC的面积.
解:因为∠ABC为直角,BC长为3,AB长为4,
所以AC2=AB2+BC2=16+9=25.
因为正方形的面积为169,
所以FC2=169.
因为AF2+AC2=144+25=169=FC2,
所以△AFC为直角三角形.
所以∠FAC为直角.
所以S△AFC=0.5AF·AC=0.5×12×5=30.
3.已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,则下列条件:①a=4,b=
?,c=
?;②a2∶b2∶c2=1∶3∶2;③∠A
∶∠B∶∠C=3∶4∶5;④∠A=2∠B=2∠C.其中能判断△ABC是直角三角形的有?( )
A.1个 ????B.2个 ????C.3个 ????D.4个
答案????C ①∵a2+b2=?=
?,c2=
?=?,
∴此三角形是直角三角形;
②∵a2∶b2∶c2=1∶3∶2,∴a2+c2=b2,∴此三角形是直角三角形;
③∵∠A∶∠B∶∠C=3∶4∶5,∴设∠A=3x,则∠B=4x,
∠C=5x,∵∠A+∠B+∠C=180°,∴3x+4x+5x=180°,
解得x=15°,∴∠A=45°,∠B=60°,∠C=75°,
∴此三角形不是直角三角形;
④∵∠A=2∠B=2∠C,∴设∠B=∠C=x,则∠A=2x,∴x+x+
2x=180°,解得x=45°,∴∠A=2x=90°,
∴此三角形是直角三角形.故选C.
∴a2+b2=c2,
作业布置;
习题1.3
1,2,3,4
选讲内容
1.如图,点E是正方形ABCD内的一点,连接AE、BE、CE,△ABE≌△CBE'.若AE=1,BE=2,CE=3,则∠BE'C= ????度.
解析 连接EE',?
∵△ABE≌△CBE',
∴AE=CE',BE=BE',∠ABE=∠CBE',
∴∠EBE'是直角,∴△EBE'是直角三角形,∠BEE'=∠BE'E=45°,
∵AE=1,BE=2,∴BE'=2,E'C=1.
∵EE'2=22+22=8,CE'=1,EC=3,∴EC2=E′C2+EE'2,
∴△EE'C是直角三角形,∴∠EE'C=90°,
∴∠BE'C=135°.
2.在△ABC中,∠A,∠B,∠C的对边分别为a
,b,c,且满足c十a=2b,c-a=0.5b,则△ABC是什么特殊三角形?
解:∵c+a=2b,c-a=
0.5b,
∴(c+a)(c-a)=b2
即a2+b2=c2,
∴c2-a2=b2
∴△ABC是直角三角形,∠C=
90°
3.如图1
-2-8,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
解:(1)AP=CQ.证明如下:
∵△ABC为等边三角形,
∴AB=BC,∠ABC=60°.
又∵∠PBQ=60°,BQ
=
BP,
∴∠ABP=∠CBQ,△BPQ为等边三角形
∴△ABP≌△CBQ
∴AP=
CQ.
(2)若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
(2)△PQC为直角三角形.理由如下:
由(1)得AP=CQ,PQ=PB,
则CQ:
PQ:
PC=3:4:5
从而CQ2
+PQ2
=PC2,
∴∠PQC=90
∴△PQC为直角三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
