人教版数学八年级上册:12.2三角形全等的判定(边边边)课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册:12.2三角形全等的判定(边边边)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 604.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
12.2
全等三角形的判定
(一)复习旧知,导入新课
能够完全重合的两个三角形叫做全等三角形。
全等三角形的对应边相等,全等三角形的对应角相等。
什么是全等三角形?
全等三角形的性质是什么?
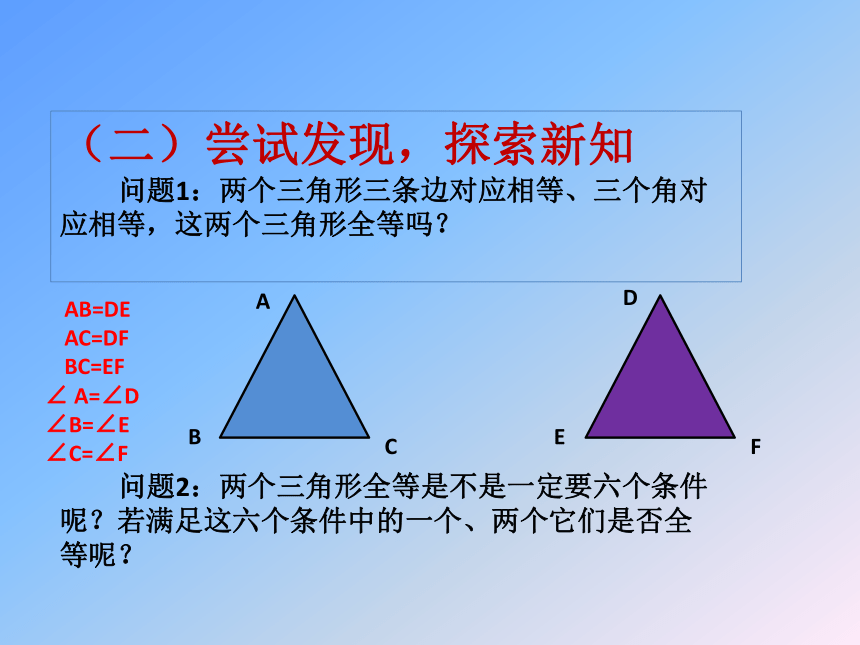
(二)尝试发现,探索新知
问题1:两个三角形三条边对应相等、三个角对应相等,这两个三角形全等吗?
问题2:两个三角形全等是不是一定要六个条件呢?若满足这六个条件中的一个、两个它们是否全等呢?
AB=DE
AC=DF
BC=EF
∠
A=∠D
∠B=∠E
∠C=∠F
A
B
C
D
E
F
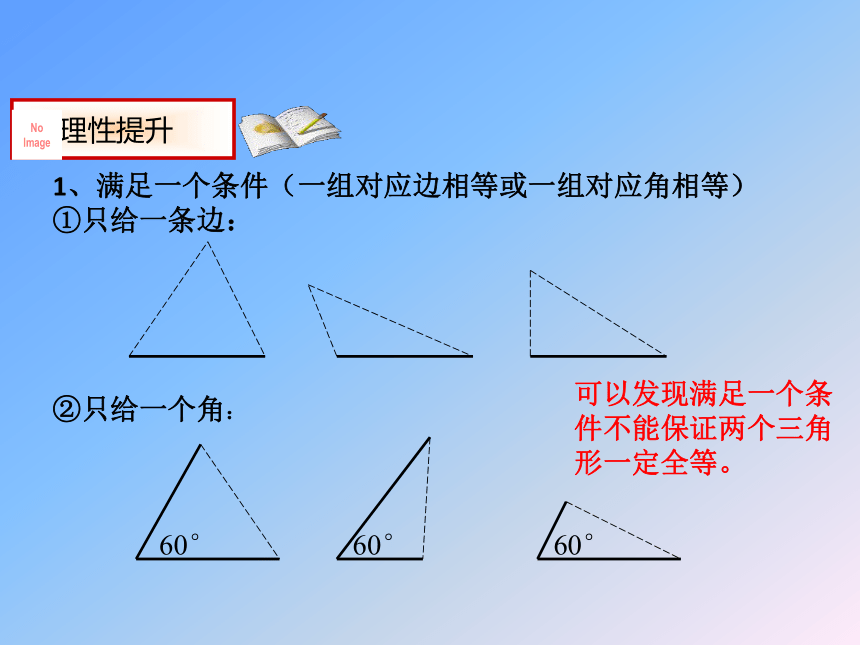
1、满足一个条件(一组对应边相等或一组对应角相等)
①只给一条边:
②只给一个角:
60°
60°
60°
可以发现满足一个条件不能保证两个三角形一定全等。
理性提升
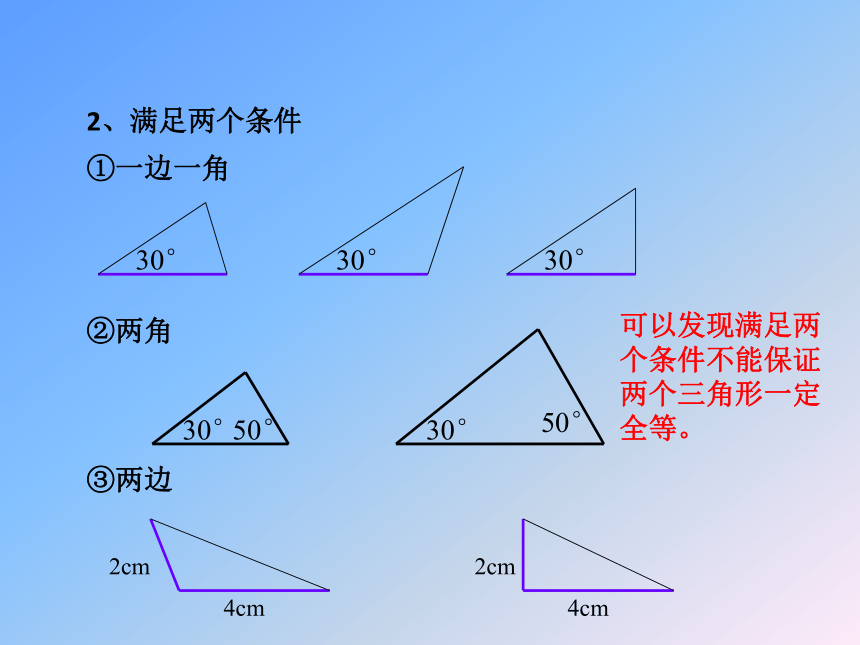
2、满足两个条件
①一边一角
30°
30°
30°
②两角
30°
30°
50°
50°
③两边
2cm
2cm
4cm
4cm
可以发现满足两个条件不能保证两个三角形一定全等。
问题3:两个三角形若满足这六个条件中的三个条件能保证它们全等吗?满足三个条件有几种情形呢?
三边对应相等
三角对应相等
两边一角对应相等
两角一边对应相等
已知三角形三条边分别是
3cm,4cm,5cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
想一想该如何画?
理性提升
(三)
动手操作,增强体验
画法:
1、画线段AB=3㎝;
2、分别以A、B为圆心,4㎝和5㎝长为半径画弧,两弧交于点C;
3、连接线段AC、BC。
像这样只用无刻度的直尺圆规作图的方法称为尺规作图。
再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
3cm
4cm
5cm
3cm
4cm
5cm
结论:两个三角形的三边对应相等,它们是全等的。
三角形全等的判定:
三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”。
在△ABC和△
DEF中
AB=DE
BC=EF
CA=FD
∴
△ABC
≌△
DEF(SSS)
A
B
C
D
E
F
例
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD
理性提升
要证明△
ABD≌
△
ACD,首先看这两个三角形的三条边是否对应相等。
方法构想
(四)
例题讲解,深刻理解
例
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD。
理性提升
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
随堂练习
(五)
随堂练习,提升认识
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
A
B
C
D
解:△ABC与△DCB全等,
理由如下:
在△ABC与△DCB中
AB=CD
BC=CB(公共边)
AC=BD
∴
△ABC≌
△DCB
(sss)
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
A
B
C
D
已知如图:AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB。
求证:△ABC
≌△
FDE
中考链接
1
(六)反思小结,体验收获
小结归纳
2
(1)如何用“边边边”判定条件证明三角形全等。
(2)证明全等三角形的书写格式和应注意的问题。
(七)布置作业,巩固提高
必做题:P37
第1、2题
选做题:P44
第9题
独立
作业
再
见
12.2
全等三角形的判定
(一)复习旧知,导入新课
能够完全重合的两个三角形叫做全等三角形。
全等三角形的对应边相等,全等三角形的对应角相等。
什么是全等三角形?
全等三角形的性质是什么?
(二)尝试发现,探索新知
问题1:两个三角形三条边对应相等、三个角对应相等,这两个三角形全等吗?
问题2:两个三角形全等是不是一定要六个条件呢?若满足这六个条件中的一个、两个它们是否全等呢?
AB=DE
AC=DF
BC=EF
∠
A=∠D
∠B=∠E
∠C=∠F
A
B
C
D
E
F
1、满足一个条件(一组对应边相等或一组对应角相等)
①只给一条边:
②只给一个角:
60°
60°
60°
可以发现满足一个条件不能保证两个三角形一定全等。
理性提升
2、满足两个条件
①一边一角
30°
30°
30°
②两角
30°
30°
50°
50°
③两边
2cm
2cm
4cm
4cm
可以发现满足两个条件不能保证两个三角形一定全等。
问题3:两个三角形若满足这六个条件中的三个条件能保证它们全等吗?满足三个条件有几种情形呢?
三边对应相等
三角对应相等
两边一角对应相等
两角一边对应相等
已知三角形三条边分别是
3cm,4cm,5cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
想一想该如何画?
理性提升
(三)
动手操作,增强体验
画法:
1、画线段AB=3㎝;
2、分别以A、B为圆心,4㎝和5㎝长为半径画弧,两弧交于点C;
3、连接线段AC、BC。
像这样只用无刻度的直尺圆规作图的方法称为尺规作图。
再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
3cm
4cm
5cm
3cm
4cm
5cm
结论:两个三角形的三边对应相等,它们是全等的。
三角形全等的判定:
三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”。
在△ABC和△
DEF中
AB=DE
BC=EF
CA=FD
∴
△ABC
≌△
DEF(SSS)
A
B
C
D
E
F
例
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD
理性提升
要证明△
ABD≌
△
ACD,首先看这两个三角形的三条边是否对应相等。
方法构想
(四)
例题讲解,深刻理解
例
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD。
理性提升
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
随堂练习
(五)
随堂练习,提升认识
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
A
B
C
D
解:△ABC与△DCB全等,
理由如下:
在△ABC与△DCB中
AB=CD
BC=CB(公共边)
AC=BD
∴
△ABC≌
△DCB
(sss)
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
A
B
C
D
已知如图:AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB。
求证:△ABC
≌△
FDE
中考链接
1
(六)反思小结,体验收获
小结归纳
2
(1)如何用“边边边”判定条件证明三角形全等。
(2)证明全等三角形的书写格式和应注意的问题。
(七)布置作业,巩固提高
必做题:P37
第1、2题
选做题:P44
第9题
独立
作业
再
见
