2019-2020学年黑龙江省哈尔滨市平房区八年级下学期期末数学试卷(五四学制) (word解析版)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨市平房区八年级下学期期末数学试卷(五四学制) (word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 970.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 06:51:37 | ||
图片预览



文档简介
2019-2020学年黑龙江省哈尔滨市平房区八年级第二学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列方程是一元二次方程的是( )
A.x+y=1 B.+2=6 C.x2=7 D.x3+4=x3
2.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
3.在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
4.下列方程中,没有实数根的是( )
A.x2﹣x﹣2=0 B.x2﹣2x+1=0 C.x2=4 D.x2﹣x+1=0
5.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
6.如图,在正方形ABCD的外侧,作等边△CDE,连接AE、BD,线段AE与DD相交于点O,则∠DOE的大小为( )
A.55° B.60° C.67.5° D.75°
7.用配方法解方程x2+6x+4=0,变形后结果正确的是( )
A.(x+3)2=﹣13 B.(x+3)2=5 C.(x+3)2=13 D.(x﹣3)2=5
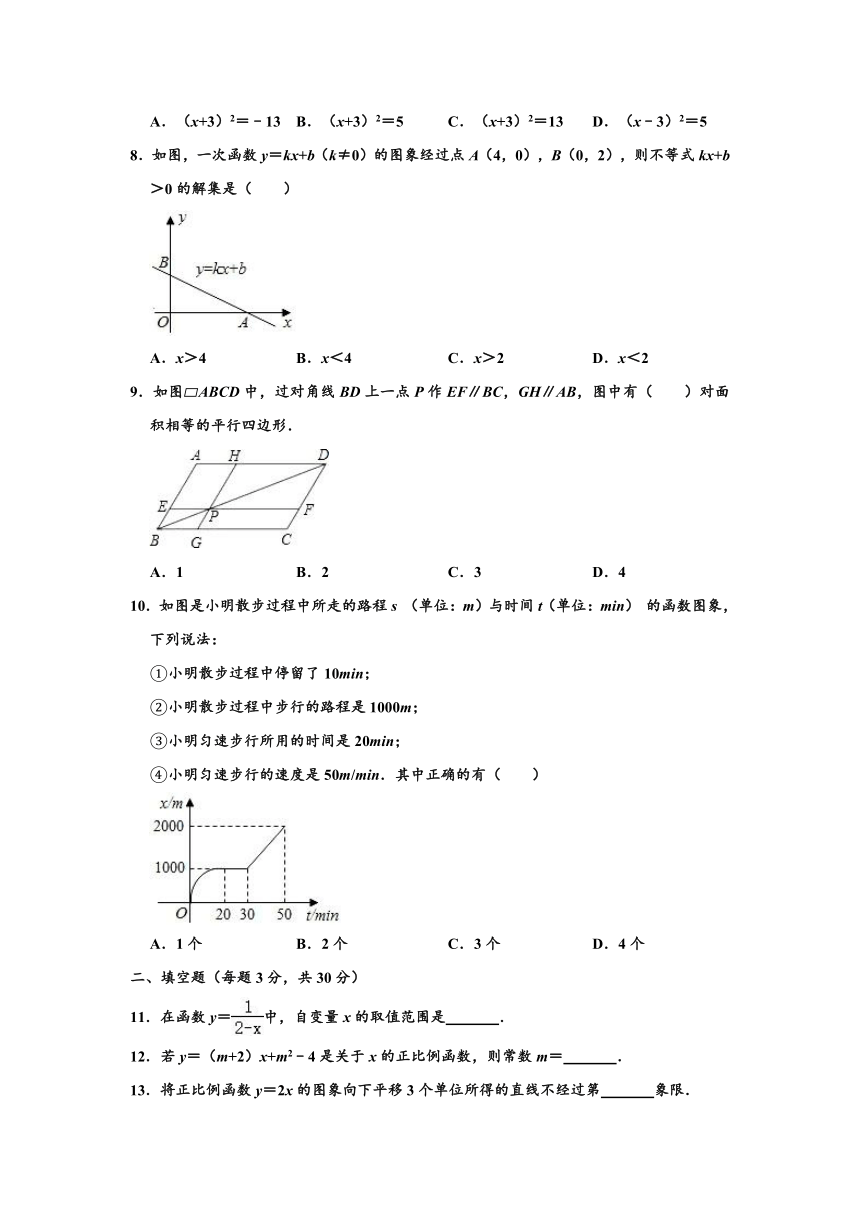
8.如图,一次函数y=kx+b(k≠0)的图象经过点A(4,0),B(0,2),则不等式kx+b>0的解集是( )
A.x>4 B.x<4 C.x>2 D.x<2
9.如图?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中有( )对面积相等的平行四边形.
A.1 B.2 C.3 D.4
10.如图是小明散步过程中所走的路程s (单位:m)与时间t(单位:min) 的函数图象,下列说法:
①小明散步过程中停留了10min;
②小明散步过程中步行的路程是1000m;
③小明匀速步行所用的时间是20min;
④小明匀速步行的速度是50m/min.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共30分)
11.在函数y=中,自变量x的取值范围是 .
12.若y=(m+2)x+m2﹣4是关于x的正比例函数,则常数m= .
13.将正比例函数y=2x的图象向下平移3个单位所得的直线不经过第 象限.
14.关于x的方程x2﹣2x﹣2a=0有一根为﹣2,则a的值是 .
15.菱形ABCD的周长为36,且∠ABC=60°,则较短的对角线AC的长为 .
16.如图,有一块矩形铁皮,长为100cm,宽50cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为1400cm2,那么铁皮各角切去的正方形的边长为 cm.
17.如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF,若CD=14,则EF的长是 .
18.如图,点E为正方形ABCD的边AD的中点,将△ABE沿BE折叠,点A'为点A的对应点,BA'的延长线交CD于点F,若四边形EDFA'的面积为8,则BE的长为 .
19.矩形ABCD的对角线交于点O,AE为△ABD的高,OD=2OE,AB=3,则AD= .
20.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=2∠ABD,若AC=2,CD=3,则线段AD的长为 .
三、简答题
21.解方程:
①x2﹣8x+12=0;
②x2﹣2x﹣8=0.
22.图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,线段的端点均在小正方形的顶点上,点C在小正方形的顶点上,连接AC、BC,并按照下面的要求分别画出满足要求的△ABC.
(1)在图1中,画出一个△ABC,使得△ABC是面积为5的直角三角形;
(2)在图2中,画出一个△ABC,使得△ABC是钝角等腰三角形.
23.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.
(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航向不变,继续航行多长时间与小岛C的距离恰好为20海里?
24.如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交 BC于点O.
(1)若∠BOD=2∠A,求证:四边形BECD是矩形;
(2)在不添加任何辅助线的情况下,请写出图中所有与△ABD全等的三角形.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
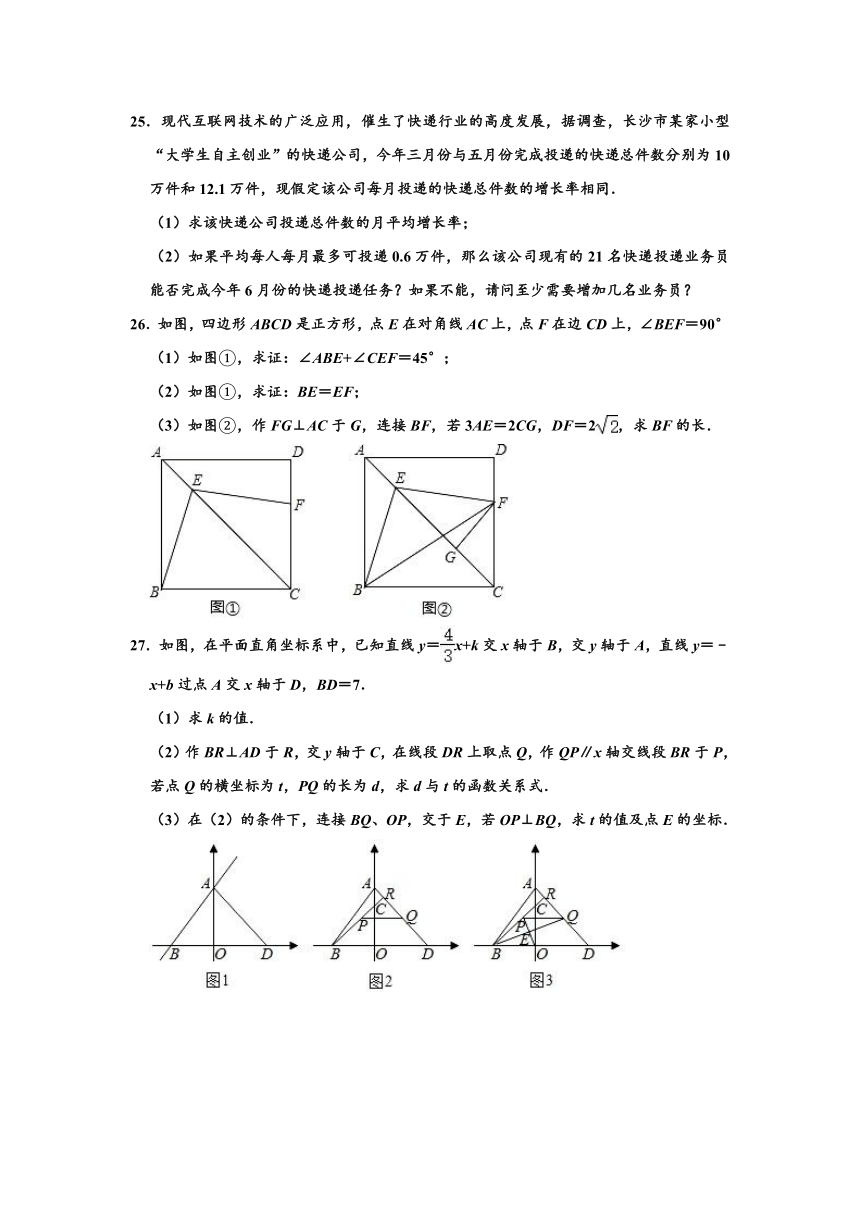
26.如图,四边形ABCD是正方形,点E在对角线AC上,点F在边CD上,∠BEF=90°
(1)如图①,求证:∠ABE+∠CEF=45°;
(2)如图①,求证:BE=EF;
(3)如图②,作FG⊥AC于G,连接BF,若3AE=2CG,DF=2,求BF的长.
27.如图,在平面直角坐标系中,已知直线y=x+k交x轴于B,交y轴于A,直线y=﹣x+b过点A交x轴于D,BD=7.
(1)求k的值.
(2)作BR⊥AD于R,交y轴于C,在线段DR上取点Q,作QP∥x轴交线段BR于P,若点Q的横坐标为t,PQ的长为d,求d与t的函数关系式.
(3)在(2)的条件下,连接BQ、OP,交于E,若OP⊥BQ,求t的值及点E的坐标.
参考答案
一、选择题(共10小题).
1.下列方程是一元二次方程的是( )
A.x+y=1 B.+2=6 C.x2=7 D.x3+4=x3
解:A、是二元一次方程,故A不符合题意;
B、是分式方程,故B不符合题意;
C、是一元二次方程,故C符合题意;
D、不是一元二次方程,故D不符合题意.
故选:C.
2.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
解:A、不是轴对称图形,符合题意;
B、是轴对称图形,不合题意;
C、是轴对称图形,不合题意;
D、是轴对称图形,不合题意.
故选:A.
3.在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
解:∵一个三角形一条直角边长是3,另一条直角边长是4,
∴斜边长==5.
故选:A.
4.下列方程中,没有实数根的是( )
A.x2﹣x﹣2=0 B.x2﹣2x+1=0 C.x2=4 D.x2﹣x+1=0
解:A、△=(﹣1)2﹣4×1×(﹣2)=9>0,方程有两个不相等的实数根,不符合题意;
B、△=(﹣2)2﹣4×1×1=0,方程有两个相等的实数根,不符合题意;
C、方程变形为x2﹣4=0,△=0﹣4×1×(﹣4)=16>0,方程有两个不相等的实数根,不符合题意;
D、△=(﹣1)2﹣4×1×1=﹣3<0,方程没有实数根,符合题意.
故选:D.
5.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
解:A、一组邻边相等的平行四边形是菱形,故选项错误;
B、正确;
C、对角线垂直的平行四边形是菱形,故选项错误;
D、两组对边平行的四边形才是平行四边形,故选项错误.
故选:B.
6.如图,在正方形ABCD的外侧,作等边△CDE,连接AE、BD,线段AE与DD相交于点O,则∠DOE的大小为( )
A.55° B.60° C.67.5° D.75°
解:∵正方形ABCD,
∴AD=DC,∠ADO=45°,∠ADC=90°
∵等边三角形DCE,
∴DC=DE,∠CDE=60°
∴AD=DE,
∴∠ADE=90°+60°=150°,
∴∠DAE=∠DEA=15°,
∴∠DOE=∠DAE+∠ADO=15°+45°=60°,
故选:B.
7.用配方法解方程x2+6x+4=0,变形后结果正确的是( )
A.(x+3)2=﹣13 B.(x+3)2=5 C.(x+3)2=13 D.(x﹣3)2=5
解:∵x2+6x+4=0,
∴x2+6x=﹣4,
则x2+6x+9=﹣4+9,即(x+3)2=5,
故选:B.
8.如图,一次函数y=kx+b(k≠0)的图象经过点A(4,0),B(0,2),则不等式kx+b>0的解集是( )
A.x>4 B.x<4 C.x>2 D.x<2
解:由题意知一次函数y=kx+b的图象经过点A(4,0),并且函数值y随x的增大而减小,
则不等式kx+b>0的解集是x<4.
故选:B.
9.如图?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中有( )对面积相等的平行四边形.
A.1 B.2 C.3 D.4
解:∵ABCD为平行四边形,BD为对角线,
∴△ABD的面积等于△BCD的面积,
同理△BGP的面积等于△EBP的面积,△PFD的面积等于△HPD的面积,
∵△BCD的面积减去△BGP的面积和PDF的面积等于平行四边形PGCF的面积,△ABD的面积减去△EBP和△HPD的面积等于平行四边形AEPH的面积.
∴?PGCF的面积等于?AEPH的面积.
∴同时加上平行四边形PFDH和BGPE,
可以得出?AEFD面积和?HGCD面积相等,?ABGH和?BCFE面积相等.
所以有3对面积相等的平行四边形.
故选:C.
10.如图是小明散步过程中所走的路程s (单位:m)与时间t(单位:min) 的函数图象,下列说法:
①小明散步过程中停留了10min;
②小明散步过程中步行的路程是1000m;
③小明匀速步行所用的时间是20min;
④小明匀速步行的速度是50m/min.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
解:由图象可知:
小明散步过程中停留的时间为:30﹣20=10(min),故①说法正确;
小明散步过程中步行的路程是2000m,故说法②错误;
小明匀速步行所用的时间为:50﹣30=20(分钟),故说法③正确;
小明匀速步行的速度为:1000÷20=50(m/min),故说法④正确.
∴正确的说法有①③④共3个.
故选:C.
二、填空题(每题3分,共30分)
11.在函数y=中,自变量x的取值范围是 x≠2 .
解:由题意得,2﹣x≠0,
解得x≠2.
故答案为:x≠2.
12.若y=(m+2)x+m2﹣4是关于x的正比例函数,则常数m= 2 .
解:∵y=(m+2)x+m2﹣4是关于x的正比例函数,
∴m+2≠0,m2﹣4=0,
解得:m=2.
故答案为:2.
13.将正比例函数y=2x的图象向下平移3个单位所得的直线不经过第 二 象限.
解:将正比例函数y=2x的图象向下平移3个单位后得到的一次函数的解析式为:y=2x﹣3,
∵k=2>0,b=﹣3<0,
∴该一次函数图象经过第一、三、四象限,即该一次函数图象不经过第二象限.
故答案为:二.
14.关于x的方程x2﹣2x﹣2a=0有一根为﹣2,则a的值是 4 .
解:把x=﹣2代入x2﹣2x﹣2a=0得4+4﹣2a=0,
解得a=4.
故答案为:4.
15.菱形ABCD的周长为36,且∠ABC=60°,则较短的对角线AC的长为 9 .
解::∵四边形ABCD是菱形,AC是对角线,
∴AB=BC=CD=AD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,
∵菱形ABCD的周长是36,
∴AB=BC=AC=9.
故答案为:9.
16.如图,有一块矩形铁皮,长为100cm,宽50cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为1400cm2,那么铁皮各角切去的正方形的边长为 15 cm.
解:设切去的正方形的边长为xcm,
则盒底的长为(100﹣2x)cm,宽为(50﹣2x)cm,
根据题意得:(100﹣2x)(50﹣2x)=1400,
展开得:x2﹣75x+900=0,
解得:x1=15,x2=60(不合题意,舍去),
则铁皮各角应切去边长为15cm的正方形.
故答案是:15.
17.如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF,若CD=14,则EF的长是 7 .
解:∵E、F分别是AD、BD的中点,
∴EF是△ABD的中位线,
∴EF=AB,
又∵在?ABCD中,CD=14,
∴AB=14,
∴EF=7,
故答案为:7.
18.如图,点E为正方形ABCD的边AD的中点,将△ABE沿BE折叠,点A'为点A的对应点,BA'的延长线交CD于点F,若四边形EDFA'的面积为8,则BE的长为 4 .
解:连结EF,
在矩形ABCD中,AB=DC,AD=BC,∠A=∠C=∠D=90°,
∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△A′BE,
∴BA′=AB,EA′=AE=ED,∠A=∠BA′E=90°,∠AEB=∠BEA′,
∴∠EA′F=∠D=90°,
在Rt△EA′F和Rt△EDF中,,
∴Rt△EA′F≌Rt△EDF(HL),
∴A'F=DF,
∵四边形EDFA'的面积为8,
∴A'F×A'E+DE×DF=8,
∴DE×DF=8,
设DF=x,AB=2a,
∴BF=A'B+A'F=2a+x,CF=2a﹣x,
根据勾股定理得,(2a+x)2﹣(2a﹣x)2=4a2,
∴x=a
∴a×a=8,
∴a=4(舍负),
∴AB=2DE=8,
∴BE==4.
故答案为:4.
19.矩形ABCD的对角线交于点O,AE为△ABD的高,OD=2OE,AB=3,则AD= 3或 .
解:①当点E在DO的延长线上时.
∵OD=2OE,OB=OD,
∴BE=OE,
∵AE⊥BD于点E,
∴AB=AO(线段的垂直平分线的性质),
又AO=BO,
∴OA=OB=AB,
∴△ABO是等边三角形,
∴∠AOB=60°,∠ODA=∠OAD=30°,
∴AD=AB=3cm,
②当点E在线段OD上时.
∵OD=2OE,
∴DE=EO,∵AE⊥OD,
∴AD=AO=OD,
∴△AOD是等边三角形,
∴∠ADB=60°,
在Rt△ABD中,AD=AB?tan30°=.
故答案为3或
20.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=2∠ABD,若AC=2,CD=3,则线段AD的长为 .
解:延长线段BA,CD相交于点E,
∵∠BDC=2∠ABD,∠BDC=∠ABD+∠BEC,
∴∠ABD=∠BED,
∴△BDE是等腰三角形,BD=DE,
又∵∠BAD=90°,
∴BA=AE,
又∵∠BCD=90°,
∴AC=BE,BE=4,
在Rt△BDC中,
∵BD2=CD2+BC2,BD2=32+BC2,
∴BC2=BD2﹣9,
在Rt△BCE中,
∵BE2=CE2+BC2,BD2=(3+DE)2+BC2,
∴BC2=(4)2﹣(3+BD)2,
即:BD2﹣9=(4)2﹣(3+BD)2,
解得BD=5,
在Rt△ABD中,
AD2=BD2﹣AB2=52﹣(2)2=.
故答案为:.
三、简答题
21.解方程:
①x2﹣8x+12=0;
②x2﹣2x﹣8=0.
解:①∵x2﹣8x+12=0,
∴(x﹣2)(x﹣6)=0,
则x﹣2=0或x﹣6=0,
解得x=2或x=6;
②∵x2﹣2x﹣8=0,
∴(x+2)(x﹣4)=0,
则x+2=0或x﹣4=0,
解得x=﹣2或x=4.
22.图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,线段的端点均在小正方形的顶点上,点C在小正方形的顶点上,连接AC、BC,并按照下面的要求分别画出满足要求的△ABC.
(1)在图1中,画出一个△ABC,使得△ABC是面积为5的直角三角形;
(2)在图2中,画出一个△ABC,使得△ABC是钝角等腰三角形.
解:(1)如图1,△ABC即为所求;
(2)如图2,△ABD即为所求.
23.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.
(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航向不变,继续航行多长时间与小岛C的距离恰好为20海里?
解:(1)作BH⊥C于H.
∵∠CBD=∠CAB+∠BCA,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠BAC=30°
∴BA=BC=30×=20(海里).
∵BH⊥AC,
∴AH=HC=AB?cos30°=10海里,
∴AC=2AH=20海里;
(2)作CG⊥AB交AB的延长线于G,
设渔船到达B处后,航向不变,继续航行到E与小岛C的距离恰好为20海里.
即CE=20海里,
∴BC=CE,
∵∠CBE=60°,
∴△BCE是等边三角形,
∴BE=20,
∴=,
∴继续航行40分钟与小岛C的距离恰好为20海里.
24.如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交 BC于点O.
(1)若∠BOD=2∠A,求证:四边形BECD是矩形;
(2)在不添加任何辅助线的情况下,请写出图中所有与△ABD全等的三角形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠A=∠DCB,
∵AB=BE,
∴CD=EB,
∴四边形BECD是平行四边形,
∴BO=CO,EO=DO,
∵∠BOD=2∠A,
∴∠BOD=2∠DCO,
∴∠DCO=∠ODC,
∴DO=CO,
∴DE=BC,
∴四边形BECD是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,BD=DB,
∴△ABD≌△CDB(SSS),
∵四边形BECD是矩形,
∴BD=CE,BE=CD,BC=DE,
∴△CDB≌△EBC(SSS),
∴△ABD≌△EBC,
同理△EBD≌△DCE,
∴图中所有与△ABD全等的三角形有△CBD,△EBC,△DCE,△BEC.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
解:(1)设该快递公司投递总件数的月平均增长率为x,根据题意得
10(1+x)2=12.1,
解得x1=0.1,x2=﹣2.1(不合题意舍去).
答:该快递公司投递总件数的月平均增长率为10%;
(2)今年6月份的快递投递任务是12.1×(1+10%)=13.31(万件).
∵平均每人每月最多可投递0.6万件,
∴21名快递投递业务员能完成的快递投递任务是:0.6×21=12.6<13.31,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
∴需要增加业务员(13.31﹣12.6)÷0.6=1≈2(人).
答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务,至少需要增加2名业务员.
26.如图,四边形ABCD是正方形,点E在对角线AC上,点F在边CD上,∠BEF=90°
(1)如图①,求证:∠ABE+∠CEF=45°;
(2)如图①,求证:BE=EF;
(3)如图②,作FG⊥AC于G,连接BF,若3AE=2CG,DF=2,求BF的长.
解:(1)如图1,作EM⊥BC于点M,EN⊥CD于点N,
∵四边形ABCD是正方形,
∴AC平分∠BCD,
∴四边形EMCN是正方形,
∴∠CEN=45°
∴AC平分∠BCD,
∴EM=EN,∠NEM=90°
∵∠BEF=90°
∴∠BEM=∠NEF
∵∠BME=∠FNE=90°
∴△BEM≌△FEN,
∴∠BEM=∠FEN,
∵EM∥AB,
∴∠BEM=∠ABE,
∴∠ABE+∠CEF=∠BEM+∠CEF=∠FEN+∠CEF=∠CEN=45°
(2)由(1)知,△BEM≌△FEN,
∴BE=EF;
(3)如图2,设CG=3x,AE=2x,
∵AC是正方形ABCD的对角线,
∴∠ACD=∠BCD=45°,
∵FG⊥AC,
∴∠CGF=90°,
∴FG=CG=3x,
∴CF=3x,
∴CD=CF+DF=3x+2=(3x+2),
在Rt△ACD中,∠ACD=45°,
∴AC=CD=6x+4,
∴CE=AC﹣AE=4x+4,过点E作EN⊥CD于N,
∴EN=CN=CE=2(x+1),
∴FN=CN﹣CF=(2﹣x),
在Rt△EFN中,根据勾股定理得,EF==×,
由(2)知,BE=EF,
∵BE⊥EF,
∴△BEF是等腰直角三角形,
∴BF=EF=2
在Rt△BCF中,BC=CD=(3x+2),CF=3x,
∴BF==2,
∴2=2,
∴x=﹣(舍)或x=1,
∴BF=2=2.
27.如图,在平面直角坐标系中,已知直线y=x+k交x轴于B,交y轴于A,直线y=﹣x+b过点A交x轴于D,BD=7.
(1)求k的值.
(2)作BR⊥AD于R,交y轴于C,在线段DR上取点Q,作QP∥x轴交线段BR于P,若点Q的横坐标为t,PQ的长为d,求d与t的函数关系式.
(3)在(2)的条件下,连接BQ、OP,交于E,若OP⊥BQ,求t的值及点E的坐标.
解:(1)∵直线y=x+k交x轴于B,交y轴于A,直线y=﹣x+b过点A交x轴于D,
∴点A(0,k),点B(﹣k,0),点D(b,0),b=k,
∵AO=k=OD,BO=k,
∵BD=BO+DO=k+k=7,
∴k=4;
(2)∵k=4,
∴直线AB解析式为:y=x+4,直线AD解析式为:y=﹣x+4,
∴点A(0,4),点B(﹣3,0),点D(4,0),
∴OA=DO,OB=3,
∴∠ODA=∠OAD=45°,
∵BR⊥AD,
∴∠RBD=45°=∠BCO,
∴BO=CO=3,
∴点C(0,3),
∴点C坐标为(0,3),
∴直线BC解析式为:y=x+3,
∵点Q的横坐标为t,
∴点Q坐标为(t,﹣t+4),
∵QP∥x轴,
∴点P(﹣t+1,﹣t+4),
∴PQ=d=t﹣(﹣t+1)=2t﹣1;
(3)∵点B(﹣3,0),点Q坐标为(t,﹣t+4),
∴直线BQ解析式为:y=x+;
∵点P(﹣t+1,﹣t+4),点O(0,0),
∴直线PO解析式为:y=x,
∵OP⊥BQ,
∴×=﹣1,
∴t=,
∴直线BQ解析式为:y=x+;直线PO解析式为:y=﹣x,
∴,
解得
∴点E坐标为(﹣,).
一、选择题(共10小题).
1.下列方程是一元二次方程的是( )
A.x+y=1 B.+2=6 C.x2=7 D.x3+4=x3
2.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
3.在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
4.下列方程中,没有实数根的是( )
A.x2﹣x﹣2=0 B.x2﹣2x+1=0 C.x2=4 D.x2﹣x+1=0
5.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
6.如图,在正方形ABCD的外侧,作等边△CDE,连接AE、BD,线段AE与DD相交于点O,则∠DOE的大小为( )
A.55° B.60° C.67.5° D.75°
7.用配方法解方程x2+6x+4=0,变形后结果正确的是( )
A.(x+3)2=﹣13 B.(x+3)2=5 C.(x+3)2=13 D.(x﹣3)2=5
8.如图,一次函数y=kx+b(k≠0)的图象经过点A(4,0),B(0,2),则不等式kx+b>0的解集是( )
A.x>4 B.x<4 C.x>2 D.x<2
9.如图?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中有( )对面积相等的平行四边形.
A.1 B.2 C.3 D.4
10.如图是小明散步过程中所走的路程s (单位:m)与时间t(单位:min) 的函数图象,下列说法:
①小明散步过程中停留了10min;
②小明散步过程中步行的路程是1000m;
③小明匀速步行所用的时间是20min;
④小明匀速步行的速度是50m/min.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共30分)
11.在函数y=中,自变量x的取值范围是 .
12.若y=(m+2)x+m2﹣4是关于x的正比例函数,则常数m= .
13.将正比例函数y=2x的图象向下平移3个单位所得的直线不经过第 象限.
14.关于x的方程x2﹣2x﹣2a=0有一根为﹣2,则a的值是 .
15.菱形ABCD的周长为36,且∠ABC=60°,则较短的对角线AC的长为 .
16.如图,有一块矩形铁皮,长为100cm,宽50cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为1400cm2,那么铁皮各角切去的正方形的边长为 cm.
17.如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF,若CD=14,则EF的长是 .
18.如图,点E为正方形ABCD的边AD的中点,将△ABE沿BE折叠,点A'为点A的对应点,BA'的延长线交CD于点F,若四边形EDFA'的面积为8,则BE的长为 .
19.矩形ABCD的对角线交于点O,AE为△ABD的高,OD=2OE,AB=3,则AD= .
20.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=2∠ABD,若AC=2,CD=3,则线段AD的长为 .
三、简答题
21.解方程:
①x2﹣8x+12=0;
②x2﹣2x﹣8=0.
22.图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,线段的端点均在小正方形的顶点上,点C在小正方形的顶点上,连接AC、BC,并按照下面的要求分别画出满足要求的△ABC.
(1)在图1中,画出一个△ABC,使得△ABC是面积为5的直角三角形;
(2)在图2中,画出一个△ABC,使得△ABC是钝角等腰三角形.
23.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.
(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航向不变,继续航行多长时间与小岛C的距离恰好为20海里?
24.如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交 BC于点O.
(1)若∠BOD=2∠A,求证:四边形BECD是矩形;
(2)在不添加任何辅助线的情况下,请写出图中所有与△ABD全等的三角形.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
26.如图,四边形ABCD是正方形,点E在对角线AC上,点F在边CD上,∠BEF=90°
(1)如图①,求证:∠ABE+∠CEF=45°;
(2)如图①,求证:BE=EF;
(3)如图②,作FG⊥AC于G,连接BF,若3AE=2CG,DF=2,求BF的长.
27.如图,在平面直角坐标系中,已知直线y=x+k交x轴于B,交y轴于A,直线y=﹣x+b过点A交x轴于D,BD=7.
(1)求k的值.
(2)作BR⊥AD于R,交y轴于C,在线段DR上取点Q,作QP∥x轴交线段BR于P,若点Q的横坐标为t,PQ的长为d,求d与t的函数关系式.
(3)在(2)的条件下,连接BQ、OP,交于E,若OP⊥BQ,求t的值及点E的坐标.
参考答案
一、选择题(共10小题).
1.下列方程是一元二次方程的是( )
A.x+y=1 B.+2=6 C.x2=7 D.x3+4=x3
解:A、是二元一次方程,故A不符合题意;
B、是分式方程,故B不符合题意;
C、是一元二次方程,故C符合题意;
D、不是一元二次方程,故D不符合题意.
故选:C.
2.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
解:A、不是轴对称图形,符合题意;
B、是轴对称图形,不合题意;
C、是轴对称图形,不合题意;
D、是轴对称图形,不合题意.
故选:A.
3.在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
解:∵一个三角形一条直角边长是3,另一条直角边长是4,
∴斜边长==5.
故选:A.
4.下列方程中,没有实数根的是( )
A.x2﹣x﹣2=0 B.x2﹣2x+1=0 C.x2=4 D.x2﹣x+1=0
解:A、△=(﹣1)2﹣4×1×(﹣2)=9>0,方程有两个不相等的实数根,不符合题意;
B、△=(﹣2)2﹣4×1×1=0,方程有两个相等的实数根,不符合题意;
C、方程变形为x2﹣4=0,△=0﹣4×1×(﹣4)=16>0,方程有两个不相等的实数根,不符合题意;
D、△=(﹣1)2﹣4×1×1=﹣3<0,方程没有实数根,符合题意.
故选:D.
5.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
解:A、一组邻边相等的平行四边形是菱形,故选项错误;
B、正确;
C、对角线垂直的平行四边形是菱形,故选项错误;
D、两组对边平行的四边形才是平行四边形,故选项错误.
故选:B.
6.如图,在正方形ABCD的外侧,作等边△CDE,连接AE、BD,线段AE与DD相交于点O,则∠DOE的大小为( )
A.55° B.60° C.67.5° D.75°
解:∵正方形ABCD,
∴AD=DC,∠ADO=45°,∠ADC=90°
∵等边三角形DCE,
∴DC=DE,∠CDE=60°
∴AD=DE,
∴∠ADE=90°+60°=150°,
∴∠DAE=∠DEA=15°,
∴∠DOE=∠DAE+∠ADO=15°+45°=60°,
故选:B.
7.用配方法解方程x2+6x+4=0,变形后结果正确的是( )
A.(x+3)2=﹣13 B.(x+3)2=5 C.(x+3)2=13 D.(x﹣3)2=5
解:∵x2+6x+4=0,
∴x2+6x=﹣4,
则x2+6x+9=﹣4+9,即(x+3)2=5,
故选:B.
8.如图,一次函数y=kx+b(k≠0)的图象经过点A(4,0),B(0,2),则不等式kx+b>0的解集是( )
A.x>4 B.x<4 C.x>2 D.x<2
解:由题意知一次函数y=kx+b的图象经过点A(4,0),并且函数值y随x的增大而减小,
则不等式kx+b>0的解集是x<4.
故选:B.
9.如图?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中有( )对面积相等的平行四边形.
A.1 B.2 C.3 D.4
解:∵ABCD为平行四边形,BD为对角线,
∴△ABD的面积等于△BCD的面积,
同理△BGP的面积等于△EBP的面积,△PFD的面积等于△HPD的面积,
∵△BCD的面积减去△BGP的面积和PDF的面积等于平行四边形PGCF的面积,△ABD的面积减去△EBP和△HPD的面积等于平行四边形AEPH的面积.
∴?PGCF的面积等于?AEPH的面积.
∴同时加上平行四边形PFDH和BGPE,
可以得出?AEFD面积和?HGCD面积相等,?ABGH和?BCFE面积相等.
所以有3对面积相等的平行四边形.
故选:C.
10.如图是小明散步过程中所走的路程s (单位:m)与时间t(单位:min) 的函数图象,下列说法:
①小明散步过程中停留了10min;
②小明散步过程中步行的路程是1000m;
③小明匀速步行所用的时间是20min;
④小明匀速步行的速度是50m/min.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
解:由图象可知:
小明散步过程中停留的时间为:30﹣20=10(min),故①说法正确;
小明散步过程中步行的路程是2000m,故说法②错误;
小明匀速步行所用的时间为:50﹣30=20(分钟),故说法③正确;
小明匀速步行的速度为:1000÷20=50(m/min),故说法④正确.
∴正确的说法有①③④共3个.
故选:C.
二、填空题(每题3分,共30分)
11.在函数y=中,自变量x的取值范围是 x≠2 .
解:由题意得,2﹣x≠0,
解得x≠2.
故答案为:x≠2.
12.若y=(m+2)x+m2﹣4是关于x的正比例函数,则常数m= 2 .
解:∵y=(m+2)x+m2﹣4是关于x的正比例函数,
∴m+2≠0,m2﹣4=0,
解得:m=2.
故答案为:2.
13.将正比例函数y=2x的图象向下平移3个单位所得的直线不经过第 二 象限.
解:将正比例函数y=2x的图象向下平移3个单位后得到的一次函数的解析式为:y=2x﹣3,
∵k=2>0,b=﹣3<0,
∴该一次函数图象经过第一、三、四象限,即该一次函数图象不经过第二象限.
故答案为:二.
14.关于x的方程x2﹣2x﹣2a=0有一根为﹣2,则a的值是 4 .
解:把x=﹣2代入x2﹣2x﹣2a=0得4+4﹣2a=0,
解得a=4.
故答案为:4.
15.菱形ABCD的周长为36,且∠ABC=60°,则较短的对角线AC的长为 9 .
解::∵四边形ABCD是菱形,AC是对角线,
∴AB=BC=CD=AD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,
∵菱形ABCD的周长是36,
∴AB=BC=AC=9.
故答案为:9.
16.如图,有一块矩形铁皮,长为100cm,宽50cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为1400cm2,那么铁皮各角切去的正方形的边长为 15 cm.
解:设切去的正方形的边长为xcm,
则盒底的长为(100﹣2x)cm,宽为(50﹣2x)cm,
根据题意得:(100﹣2x)(50﹣2x)=1400,
展开得:x2﹣75x+900=0,
解得:x1=15,x2=60(不合题意,舍去),
则铁皮各角应切去边长为15cm的正方形.
故答案是:15.
17.如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF,若CD=14,则EF的长是 7 .
解:∵E、F分别是AD、BD的中点,
∴EF是△ABD的中位线,
∴EF=AB,
又∵在?ABCD中,CD=14,
∴AB=14,
∴EF=7,
故答案为:7.
18.如图,点E为正方形ABCD的边AD的中点,将△ABE沿BE折叠,点A'为点A的对应点,BA'的延长线交CD于点F,若四边形EDFA'的面积为8,则BE的长为 4 .
解:连结EF,
在矩形ABCD中,AB=DC,AD=BC,∠A=∠C=∠D=90°,
∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△A′BE,
∴BA′=AB,EA′=AE=ED,∠A=∠BA′E=90°,∠AEB=∠BEA′,
∴∠EA′F=∠D=90°,
在Rt△EA′F和Rt△EDF中,,
∴Rt△EA′F≌Rt△EDF(HL),
∴A'F=DF,
∵四边形EDFA'的面积为8,
∴A'F×A'E+DE×DF=8,
∴DE×DF=8,
设DF=x,AB=2a,
∴BF=A'B+A'F=2a+x,CF=2a﹣x,
根据勾股定理得,(2a+x)2﹣(2a﹣x)2=4a2,
∴x=a
∴a×a=8,
∴a=4(舍负),
∴AB=2DE=8,
∴BE==4.
故答案为:4.
19.矩形ABCD的对角线交于点O,AE为△ABD的高,OD=2OE,AB=3,则AD= 3或 .
解:①当点E在DO的延长线上时.
∵OD=2OE,OB=OD,
∴BE=OE,
∵AE⊥BD于点E,
∴AB=AO(线段的垂直平分线的性质),
又AO=BO,
∴OA=OB=AB,
∴△ABO是等边三角形,
∴∠AOB=60°,∠ODA=∠OAD=30°,
∴AD=AB=3cm,
②当点E在线段OD上时.
∵OD=2OE,
∴DE=EO,∵AE⊥OD,
∴AD=AO=OD,
∴△AOD是等边三角形,
∴∠ADB=60°,
在Rt△ABD中,AD=AB?tan30°=.
故答案为3或
20.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=2∠ABD,若AC=2,CD=3,则线段AD的长为 .
解:延长线段BA,CD相交于点E,
∵∠BDC=2∠ABD,∠BDC=∠ABD+∠BEC,
∴∠ABD=∠BED,
∴△BDE是等腰三角形,BD=DE,
又∵∠BAD=90°,
∴BA=AE,
又∵∠BCD=90°,
∴AC=BE,BE=4,
在Rt△BDC中,
∵BD2=CD2+BC2,BD2=32+BC2,
∴BC2=BD2﹣9,
在Rt△BCE中,
∵BE2=CE2+BC2,BD2=(3+DE)2+BC2,
∴BC2=(4)2﹣(3+BD)2,
即:BD2﹣9=(4)2﹣(3+BD)2,
解得BD=5,
在Rt△ABD中,
AD2=BD2﹣AB2=52﹣(2)2=.
故答案为:.
三、简答题
21.解方程:
①x2﹣8x+12=0;
②x2﹣2x﹣8=0.
解:①∵x2﹣8x+12=0,
∴(x﹣2)(x﹣6)=0,
则x﹣2=0或x﹣6=0,
解得x=2或x=6;
②∵x2﹣2x﹣8=0,
∴(x+2)(x﹣4)=0,
则x+2=0或x﹣4=0,
解得x=﹣2或x=4.
22.图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,线段的端点均在小正方形的顶点上,点C在小正方形的顶点上,连接AC、BC,并按照下面的要求分别画出满足要求的△ABC.
(1)在图1中,画出一个△ABC,使得△ABC是面积为5的直角三角形;
(2)在图2中,画出一个△ABC,使得△ABC是钝角等腰三角形.
解:(1)如图1,△ABC即为所求;
(2)如图2,△ABD即为所求.
23.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.
(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航向不变,继续航行多长时间与小岛C的距离恰好为20海里?
解:(1)作BH⊥C于H.
∵∠CBD=∠CAB+∠BCA,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠BAC=30°
∴BA=BC=30×=20(海里).
∵BH⊥AC,
∴AH=HC=AB?cos30°=10海里,
∴AC=2AH=20海里;
(2)作CG⊥AB交AB的延长线于G,
设渔船到达B处后,航向不变,继续航行到E与小岛C的距离恰好为20海里.
即CE=20海里,
∴BC=CE,
∵∠CBE=60°,
∴△BCE是等边三角形,
∴BE=20,
∴=,
∴继续航行40分钟与小岛C的距离恰好为20海里.
24.如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交 BC于点O.
(1)若∠BOD=2∠A,求证:四边形BECD是矩形;
(2)在不添加任何辅助线的情况下,请写出图中所有与△ABD全等的三角形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠A=∠DCB,
∵AB=BE,
∴CD=EB,
∴四边形BECD是平行四边形,
∴BO=CO,EO=DO,
∵∠BOD=2∠A,
∴∠BOD=2∠DCO,
∴∠DCO=∠ODC,
∴DO=CO,
∴DE=BC,
∴四边形BECD是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,BD=DB,
∴△ABD≌△CDB(SSS),
∵四边形BECD是矩形,
∴BD=CE,BE=CD,BC=DE,
∴△CDB≌△EBC(SSS),
∴△ABD≌△EBC,
同理△EBD≌△DCE,
∴图中所有与△ABD全等的三角形有△CBD,△EBC,△DCE,△BEC.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
解:(1)设该快递公司投递总件数的月平均增长率为x,根据题意得
10(1+x)2=12.1,
解得x1=0.1,x2=﹣2.1(不合题意舍去).
答:该快递公司投递总件数的月平均增长率为10%;
(2)今年6月份的快递投递任务是12.1×(1+10%)=13.31(万件).
∵平均每人每月最多可投递0.6万件,
∴21名快递投递业务员能完成的快递投递任务是:0.6×21=12.6<13.31,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
∴需要增加业务员(13.31﹣12.6)÷0.6=1≈2(人).
答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务,至少需要增加2名业务员.
26.如图,四边形ABCD是正方形,点E在对角线AC上,点F在边CD上,∠BEF=90°
(1)如图①,求证:∠ABE+∠CEF=45°;
(2)如图①,求证:BE=EF;
(3)如图②,作FG⊥AC于G,连接BF,若3AE=2CG,DF=2,求BF的长.
解:(1)如图1,作EM⊥BC于点M,EN⊥CD于点N,
∵四边形ABCD是正方形,
∴AC平分∠BCD,
∴四边形EMCN是正方形,
∴∠CEN=45°
∴AC平分∠BCD,
∴EM=EN,∠NEM=90°
∵∠BEF=90°
∴∠BEM=∠NEF
∵∠BME=∠FNE=90°
∴△BEM≌△FEN,
∴∠BEM=∠FEN,
∵EM∥AB,
∴∠BEM=∠ABE,
∴∠ABE+∠CEF=∠BEM+∠CEF=∠FEN+∠CEF=∠CEN=45°
(2)由(1)知,△BEM≌△FEN,
∴BE=EF;
(3)如图2,设CG=3x,AE=2x,
∵AC是正方形ABCD的对角线,
∴∠ACD=∠BCD=45°,
∵FG⊥AC,
∴∠CGF=90°,
∴FG=CG=3x,
∴CF=3x,
∴CD=CF+DF=3x+2=(3x+2),
在Rt△ACD中,∠ACD=45°,
∴AC=CD=6x+4,
∴CE=AC﹣AE=4x+4,过点E作EN⊥CD于N,
∴EN=CN=CE=2(x+1),
∴FN=CN﹣CF=(2﹣x),
在Rt△EFN中,根据勾股定理得,EF==×,
由(2)知,BE=EF,
∵BE⊥EF,
∴△BEF是等腰直角三角形,
∴BF=EF=2
在Rt△BCF中,BC=CD=(3x+2),CF=3x,
∴BF==2,
∴2=2,
∴x=﹣(舍)或x=1,
∴BF=2=2.
27.如图,在平面直角坐标系中,已知直线y=x+k交x轴于B,交y轴于A,直线y=﹣x+b过点A交x轴于D,BD=7.
(1)求k的值.
(2)作BR⊥AD于R,交y轴于C,在线段DR上取点Q,作QP∥x轴交线段BR于P,若点Q的横坐标为t,PQ的长为d,求d与t的函数关系式.
(3)在(2)的条件下,连接BQ、OP,交于E,若OP⊥BQ,求t的值及点E的坐标.
解:(1)∵直线y=x+k交x轴于B,交y轴于A,直线y=﹣x+b过点A交x轴于D,
∴点A(0,k),点B(﹣k,0),点D(b,0),b=k,
∵AO=k=OD,BO=k,
∵BD=BO+DO=k+k=7,
∴k=4;
(2)∵k=4,
∴直线AB解析式为:y=x+4,直线AD解析式为:y=﹣x+4,
∴点A(0,4),点B(﹣3,0),点D(4,0),
∴OA=DO,OB=3,
∴∠ODA=∠OAD=45°,
∵BR⊥AD,
∴∠RBD=45°=∠BCO,
∴BO=CO=3,
∴点C(0,3),
∴点C坐标为(0,3),
∴直线BC解析式为:y=x+3,
∵点Q的横坐标为t,
∴点Q坐标为(t,﹣t+4),
∵QP∥x轴,
∴点P(﹣t+1,﹣t+4),
∴PQ=d=t﹣(﹣t+1)=2t﹣1;
(3)∵点B(﹣3,0),点Q坐标为(t,﹣t+4),
∴直线BQ解析式为:y=x+;
∵点P(﹣t+1,﹣t+4),点O(0,0),
∴直线PO解析式为:y=x,
∵OP⊥BQ,
∴×=﹣1,
∴t=,
∴直线BQ解析式为:y=x+;直线PO解析式为:y=﹣x,
∴,
解得
∴点E坐标为(﹣,).
同课章节目录
