2020-2021学年人教A版数学高一上学期1.1集合的含义与表示 学案
文档属性
| 名称 | 2020-2021学年人教A版数学高一上学期1.1集合的含义与表示 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1004.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 15:46:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.1集合的含义与表示导学案
学生姓名
班级
序号
课题内容
集合的概念
学习目标与核心素养
学习目标:1.了解元素与集合的含义及其记法;2.理解集合元素的性质以及集合相等的概念;3.理解集合与元素的关系及其记法;4.识记数学中一些常用的数集及其记法;5.会运用集合的表示方法.核心素养:1.数学抽象:集合概念的理解,描述法表示集合的方法;2.逻辑推理:集合的互异性的辨析与应用;3.数学运算:集合相等时的参数计算,集合的描述法转化为列举法时的运算;4.数据分析:元素属于集合对应的参数满足的条件;5.数学建模:用集合思想对实际生活中的对象进行判断与归类.
学习重点
集合的基本概念,集合中元素的三个特性,元素与集合的关系,集合的表示方法
学习难点
元素与集合的关系,选择适当的方法表示具体问题中的集合.
阅读课本
2-5
页,填写.
1.元素与集合的概念
(1)
元素:一般地,把
__________统称为元素.元素常用小写的拉丁字母
a,b,c,…,z表示.
(2)
集合:把一些元素组成的
________叫做集合
(简称为
_______).集合通常用大写的拉丁字母
A,
B,C,…,Z表示.
(3)
元素的特性:
_________、__________
、___________.
(4)
集合相等:只要构成两个集合的
_______是一样的,就称这两个集合是相等的.
2.元素与集合的关系
关系
语言描述
记法
读法
属于
a
是集合
A
中的元素
a___A
a
属于集合
A
不属于
a
不是集合
A
中的元素
a___A
a
属于集合
A
3.数学中一些常用的数集的字母表示
数集
非负整数集或自然数集
正整数集
整数集
有理数集
实数集
字母表示
4.列举法
把集合的元素
_____________,并用花括号
“{
}”括起来表示集合的方法叫做列举法.
5.描述法
(1)
定义:用集合所含元素的
___________表示集合的方法.
(2)
具体方法:在花括号内先写上表示这个集合元素的
__________及____________,再画一条竖
线,在竖线后写出这个集合中元素所具有的
_________.
1.
(3)
金星汽车厂2003年生产的所有汽车;
(4)
2004年1月1日之前与中华人民共和国建立外交关系的所有国家;
(5)
所有的正方形;
(6)
到直线l的距离等于定长d的所有的点;
(7)
方程x?+3
x-2=0的所有实数根;
(8)
新华中学2004年9月入学的所有的高一学生.
上面的例(3)
到例(8)
都能组成集合吗?它们的元素分别是什么?
2.
判断以下元素的全体是否组成集合,井说明理由:
(1)
大于3小于11的偶数;
(2)
我国的小河流.
3.
(1)
你能用自然语言描述集合{2,
4,
6,
8}吗?
(2)
你能用列举法表示不等式x-7<3的解集吗?
4.
(1)
结合上述实例,试比较用自然语言、列举法和描述法表示集合时各自的特点和适用的对象.
(2)
自己举出几个集合的例子,并分别用自然语言、列举法和措述法表示出来.
探究点一:集合的含义与判定
例
1
考查下列每组对象,能构成一个集合的是
(
)
①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2018年第
23届冬季奥运会金牌获得者.
A.③④
B.②③④
C.②③
D.②④
探究点二:元素与集合的关系及集合元素的互异性辨析
例
2
(1)下列关系中,正确的有(
)
①12∈R;②
|-3|∈N;③
|-
3|∈
Q.
A.0
个
B.1
个
C.2
个
D.3
个
(2)集合
A中的元素x满足3-x∈N,x∈N,则集合A
中的元素为
________.
例
3
已知集合A含有两个元素a和a?,若
1∈A,则实数a的值为
________.
变式
1.
[变条件
]本例若将条件
“1∈A”改为
“2∈
A”,其他条件不变,求实数
a
的值.
变式
2.
[变条件
]本例若去掉条件
“1∈A”,其他条件不变,则实数
a的取值范围是什么?
变式
3.[变条件
]已知集合
A
含有两个元素
1
和
a?,若
“a∈
A”,求实数
a
的值.
探究点三:集合的表示方法
例
4
用列举法表示下列集合.
(1)不大于
10
的非负偶数组成的集合;
(2)方程
x?=x
的所有实数解组成的集合;
(3)直线
y=2x+1
与
y
轴的交点所组成的集合.
例
5
用描述法表示下列集合:
(1)被3除余
1的正整数的集合;
(2)坐标平面内第一象限的点的集合;
(3)大于
4
的所有偶数.
例
6
(1)若集合
A={
x∈
R|ax?+2x+1=0,a∈
R}
中只有一个元素,则
a=
(
)
A.1
B.2
C.0
D.0
或
1
(2)设12∈
{x
|x?-ax-72=0},则集合{x|
x?-5
x-a=0}中所有元素之积为
________.
例
7
用描述法表示抛物线
y=x?+1
上的点构成的集合.
变式
1.
[变条件,变设问
]本题中点的集合若改为
“{x|y=x?+1}
”,则集合中的元素是什么?
变式
2.
[变条件,变设问
]本题中点的集合若改为“{y|y=x?+1}
”,则集合中的元素是什么?
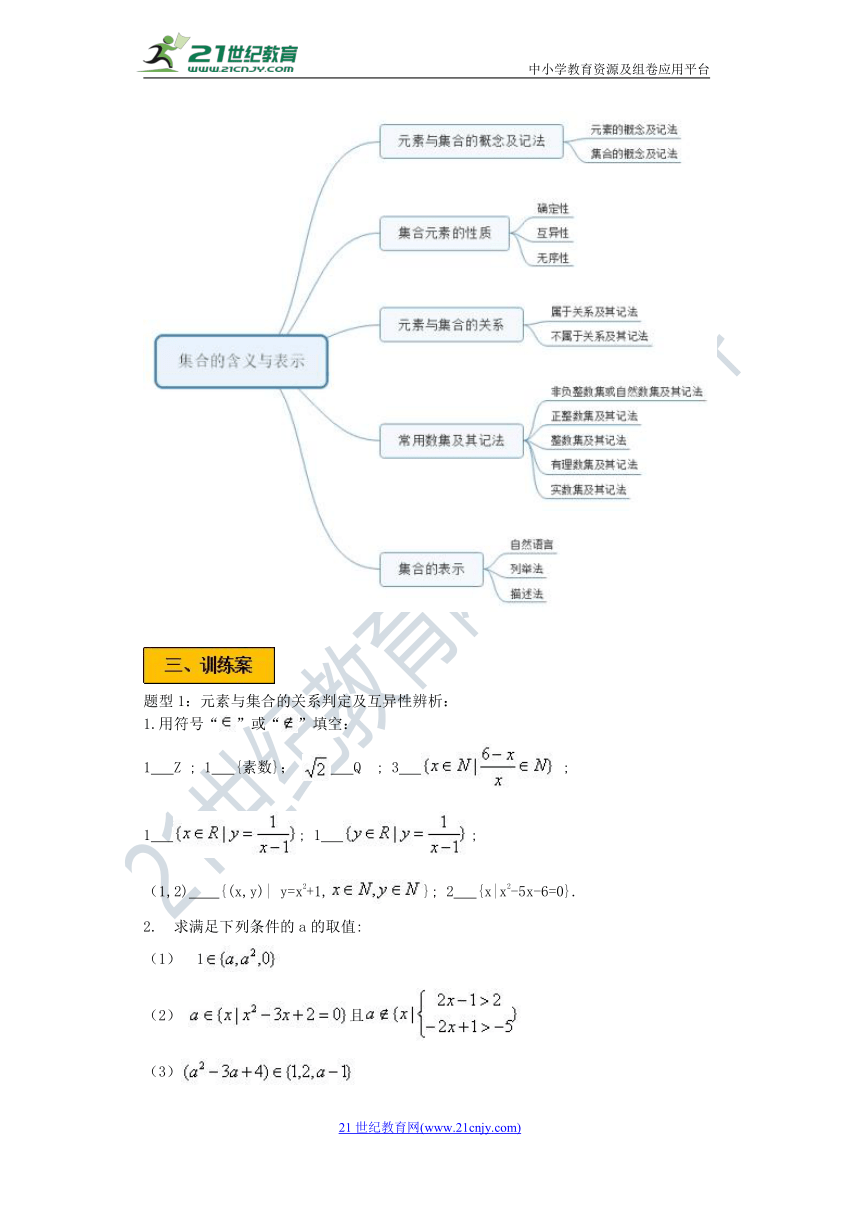
题型1:元素与集合的关系判定及互异性辨析:
1.用符号“”或“”填空:
1
Z
;
1
{素数};
Q
;
3
;
1
;
1
;
(1,2)
{(x,y)|
y=x2+1,};
2
{x|x2-5x-6=0}.
2.
求满足下列条件的a的取值:
(1)
1
(2)
且
(3)
(4)
集合是单元素集
(5)集合各元素之和等于-1.
题型2:集合的表示方法
3.
用列举法写出下列集合:
(1)
A=;
(2)
B=;
(3)
C=
4.
用描述法表示下列集合:
(1)
直角坐标平面内坐标轴上的点集;
(2)
图中阴影部分的点(含边界上的点)组成的集合.
《集合的含义与表示》
这节课作为高中的起始课,
其特点是概
念多,符号多。教学任务是:使学生了解集合的含义,体会集合元素
与集合的属于关系,
知道数集及其专用符号,
了解集合中元素的确定
性、互异性、无序性,会用集合语言表示数学对象.针对教学任务及
其特点,
在教学过程中,
我首先对集合及其创始人康托做了一个介绍,
接着介绍了集合在数学中的基础地位,
让同学们感到学好这堂课的重
要性(目的是以学生为中心,充分调动学生的学习积极性)其次,通
过一些问题引导学生阅读课本相关内容,
并结合学生已有知识经验及
课本知识让学生们举出生活中的一些例子,
进而再举出数学中这样的
例子(目的之一是通过实例了解集合的含义,
体会元素与集合的关系;
二是让同学们体会数学知识来源于实践)
,对于集合中元素的特点这
一教学难点的教学,
我仍然采用一些学生熟悉的例子引导学生理解和
掌握.在例题的选取上我结合学生的认知能力,
多角度多层次的选择
例题以使学生掌握本节知识.
答案:
预习案答案:
(1)研究对象(2)总体
集(3)确定性
互异性
无序性(4)元素
或
一一列举出来
(1)共同特征(2)一般符号
取值(或变化)范围
共同特征
列出我的疑惑答案:
1.
能,元素是金星汽车厂2003年生产的每一辆汽车;
能,元素是
2004年1月1日之前与中华人民共和国建立外交关系的每一个国家;
能,元素是每一个正方形;
能,元素是到直线l的距离等于定长d的每一个点;
能,
元素是方程x?+3
x-2=0的每一个实数根;
能,元素是新华中学2004年9月入学的每一个高一学生.
(1)是,因为
大于3小于11的偶数是确定的;
(2)否,因为
我国的小河流是不确定的.
3.
能,大于1小于9的所有偶数组成的集合;
不能.
4.
集合的3种表示方法
自然语言
列举法
描述法
各自的特点
用文字叙述的形式描述集合
元素个数较少或者元素个数较多,元素之间有明显规律的集合
用集合所含元素的共同特征表示集合
适用的对象
具有某种特定性质的具体的或抽象的对象汇总而成的集体
元素个数为有限个时,将集合的元素逐一列举出来
;元素个数为无限个时,将它们的变化规律表示出来
集合中元素有共同特征
自然语言、列举法和描述法表示集合时各自的特点和适用的对象如下表所示:
(2)举例列表如下:
自然语言
小于9的正奇数集合
能被3整除且小于10的自然数集合
列举法
{1,,3,5,7}
{0,3,6,9}
描述法
探究案答案:
B
(1)D(2)0,1,2,3
-1
变式
1.a=2或.
变式
2..
变式
3.a=0.
(1){0,2,4,6,8,10}
{-1,0,1}
{(0,1)}
(1)
{(x,y)|x>0,y>0}
(1)D
-6
{(x,y)|y=x?+1}
变式
1.元素是满足y=x?+1的每一个实数x.
变式2.元素是满足y=x?+1的每一个实数y.
训练案答案:
;;;;;;
2.(1)a=-1;
(2)a=3;
(3)a=1或2;
(4)a=-1;
(5)a=.
3.(1)A={1,2,3,6};
(2)B={1,4,5};
C={0,5,8,11}.
4.(1){(x,y)|xy=0};
{(x,y)|0≤x≤4,0≤y≤2}.
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
1.1集合的含义与表示导学案
学生姓名
班级
序号
课题内容
集合的概念
学习目标与核心素养
学习目标:1.了解元素与集合的含义及其记法;2.理解集合元素的性质以及集合相等的概念;3.理解集合与元素的关系及其记法;4.识记数学中一些常用的数集及其记法;5.会运用集合的表示方法.核心素养:1.数学抽象:集合概念的理解,描述法表示集合的方法;2.逻辑推理:集合的互异性的辨析与应用;3.数学运算:集合相等时的参数计算,集合的描述法转化为列举法时的运算;4.数据分析:元素属于集合对应的参数满足的条件;5.数学建模:用集合思想对实际生活中的对象进行判断与归类.
学习重点
集合的基本概念,集合中元素的三个特性,元素与集合的关系,集合的表示方法
学习难点
元素与集合的关系,选择适当的方法表示具体问题中的集合.
阅读课本
2-5
页,填写.
1.元素与集合的概念
(1)
元素:一般地,把
__________统称为元素.元素常用小写的拉丁字母
a,b,c,…,z表示.
(2)
集合:把一些元素组成的
________叫做集合
(简称为
_______).集合通常用大写的拉丁字母
A,
B,C,…,Z表示.
(3)
元素的特性:
_________、__________
、___________.
(4)
集合相等:只要构成两个集合的
_______是一样的,就称这两个集合是相等的.
2.元素与集合的关系
关系
语言描述
记法
读法
属于
a
是集合
A
中的元素
a___A
a
属于集合
A
不属于
a
不是集合
A
中的元素
a___A
a
属于集合
A
3.数学中一些常用的数集的字母表示
数集
非负整数集或自然数集
正整数集
整数集
有理数集
实数集
字母表示
4.列举法
把集合的元素
_____________,并用花括号
“{
}”括起来表示集合的方法叫做列举法.
5.描述法
(1)
定义:用集合所含元素的
___________表示集合的方法.
(2)
具体方法:在花括号内先写上表示这个集合元素的
__________及____________,再画一条竖
线,在竖线后写出这个集合中元素所具有的
_________.
1.
(3)
金星汽车厂2003年生产的所有汽车;
(4)
2004年1月1日之前与中华人民共和国建立外交关系的所有国家;
(5)
所有的正方形;
(6)
到直线l的距离等于定长d的所有的点;
(7)
方程x?+3
x-2=0的所有实数根;
(8)
新华中学2004年9月入学的所有的高一学生.
上面的例(3)
到例(8)
都能组成集合吗?它们的元素分别是什么?
2.
判断以下元素的全体是否组成集合,井说明理由:
(1)
大于3小于11的偶数;
(2)
我国的小河流.
3.
(1)
你能用自然语言描述集合{2,
4,
6,
8}吗?
(2)
你能用列举法表示不等式x-7<3的解集吗?
4.
(1)
结合上述实例,试比较用自然语言、列举法和描述法表示集合时各自的特点和适用的对象.
(2)
自己举出几个集合的例子,并分别用自然语言、列举法和措述法表示出来.
探究点一:集合的含义与判定
例
1
考查下列每组对象,能构成一个集合的是
(
)
①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2018年第
23届冬季奥运会金牌获得者.
A.③④
B.②③④
C.②③
D.②④
探究点二:元素与集合的关系及集合元素的互异性辨析
例
2
(1)下列关系中,正确的有(
)
①12∈R;②
|-3|∈N;③
|-
3|∈
Q.
A.0
个
B.1
个
C.2
个
D.3
个
(2)集合
A中的元素x满足3-x∈N,x∈N,则集合A
中的元素为
________.
例
3
已知集合A含有两个元素a和a?,若
1∈A,则实数a的值为
________.
变式
1.
[变条件
]本例若将条件
“1∈A”改为
“2∈
A”,其他条件不变,求实数
a
的值.
变式
2.
[变条件
]本例若去掉条件
“1∈A”,其他条件不变,则实数
a的取值范围是什么?
变式
3.[变条件
]已知集合
A
含有两个元素
1
和
a?,若
“a∈
A”,求实数
a
的值.
探究点三:集合的表示方法
例
4
用列举法表示下列集合.
(1)不大于
10
的非负偶数组成的集合;
(2)方程
x?=x
的所有实数解组成的集合;
(3)直线
y=2x+1
与
y
轴的交点所组成的集合.
例
5
用描述法表示下列集合:
(1)被3除余
1的正整数的集合;
(2)坐标平面内第一象限的点的集合;
(3)大于
4
的所有偶数.
例
6
(1)若集合
A={
x∈
R|ax?+2x+1=0,a∈
R}
中只有一个元素,则
a=
(
)
A.1
B.2
C.0
D.0
或
1
(2)设12∈
{x
|x?-ax-72=0},则集合{x|
x?-5
x-a=0}中所有元素之积为
________.
例
7
用描述法表示抛物线
y=x?+1
上的点构成的集合.
变式
1.
[变条件,变设问
]本题中点的集合若改为
“{x|y=x?+1}
”,则集合中的元素是什么?
变式
2.
[变条件,变设问
]本题中点的集合若改为“{y|y=x?+1}
”,则集合中的元素是什么?
题型1:元素与集合的关系判定及互异性辨析:
1.用符号“”或“”填空:
1
Z
;
1
{素数};
Q
;
3
;
1
;
1
;
(1,2)
{(x,y)|
y=x2+1,};
2
{x|x2-5x-6=0}.
2.
求满足下列条件的a的取值:
(1)
1
(2)
且
(3)
(4)
集合是单元素集
(5)集合各元素之和等于-1.
题型2:集合的表示方法
3.
用列举法写出下列集合:
(1)
A=;
(2)
B=;
(3)
C=
4.
用描述法表示下列集合:
(1)
直角坐标平面内坐标轴上的点集;
(2)
图中阴影部分的点(含边界上的点)组成的集合.
《集合的含义与表示》
这节课作为高中的起始课,
其特点是概
念多,符号多。教学任务是:使学生了解集合的含义,体会集合元素
与集合的属于关系,
知道数集及其专用符号,
了解集合中元素的确定
性、互异性、无序性,会用集合语言表示数学对象.针对教学任务及
其特点,
在教学过程中,
我首先对集合及其创始人康托做了一个介绍,
接着介绍了集合在数学中的基础地位,
让同学们感到学好这堂课的重
要性(目的是以学生为中心,充分调动学生的学习积极性)其次,通
过一些问题引导学生阅读课本相关内容,
并结合学生已有知识经验及
课本知识让学生们举出生活中的一些例子,
进而再举出数学中这样的
例子(目的之一是通过实例了解集合的含义,
体会元素与集合的关系;
二是让同学们体会数学知识来源于实践)
,对于集合中元素的特点这
一教学难点的教学,
我仍然采用一些学生熟悉的例子引导学生理解和
掌握.在例题的选取上我结合学生的认知能力,
多角度多层次的选择
例题以使学生掌握本节知识.
答案:
预习案答案:
(1)研究对象(2)总体
集(3)确定性
互异性
无序性(4)元素
或
一一列举出来
(1)共同特征(2)一般符号
取值(或变化)范围
共同特征
列出我的疑惑答案:
1.
能,元素是金星汽车厂2003年生产的每一辆汽车;
能,元素是
2004年1月1日之前与中华人民共和国建立外交关系的每一个国家;
能,元素是每一个正方形;
能,元素是到直线l的距离等于定长d的每一个点;
能,
元素是方程x?+3
x-2=0的每一个实数根;
能,元素是新华中学2004年9月入学的每一个高一学生.
(1)是,因为
大于3小于11的偶数是确定的;
(2)否,因为
我国的小河流是不确定的.
3.
能,大于1小于9的所有偶数组成的集合;
不能.
4.
集合的3种表示方法
自然语言
列举法
描述法
各自的特点
用文字叙述的形式描述集合
元素个数较少或者元素个数较多,元素之间有明显规律的集合
用集合所含元素的共同特征表示集合
适用的对象
具有某种特定性质的具体的或抽象的对象汇总而成的集体
元素个数为有限个时,将集合的元素逐一列举出来
;元素个数为无限个时,将它们的变化规律表示出来
集合中元素有共同特征
自然语言、列举法和描述法表示集合时各自的特点和适用的对象如下表所示:
(2)举例列表如下:
自然语言
小于9的正奇数集合
能被3整除且小于10的自然数集合
列举法
{1,,3,5,7}
{0,3,6,9}
描述法
探究案答案:
B
(1)D(2)0,1,2,3
-1
变式
1.a=2或.
变式
2..
变式
3.a=0.
(1){0,2,4,6,8,10}
{-1,0,1}
{(0,1)}
(1)
{(x,y)|x>0,y>0}
(1)D
-6
{(x,y)|y=x?+1}
变式
1.元素是满足y=x?+1的每一个实数x.
变式2.元素是满足y=x?+1的每一个实数y.
训练案答案:
;;;;;;
2.(1)a=-1;
(2)a=3;
(3)a=1或2;
(4)a=-1;
(5)a=.
3.(1)A={1,2,3,6};
(2)B={1,4,5};
C={0,5,8,11}.
4.(1){(x,y)|xy=0};
{(x,y)|0≤x≤4,0≤y≤2}.
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
