人教版九年级下册数学27.2.1相似三角形的判定 课件(45张PPT)
文档属性
| 名称 | 人教版九年级下册数学27.2.1相似三角形的判定 课件(45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 15:31:13 | ||
图片预览

文档简介
(共45张PPT)
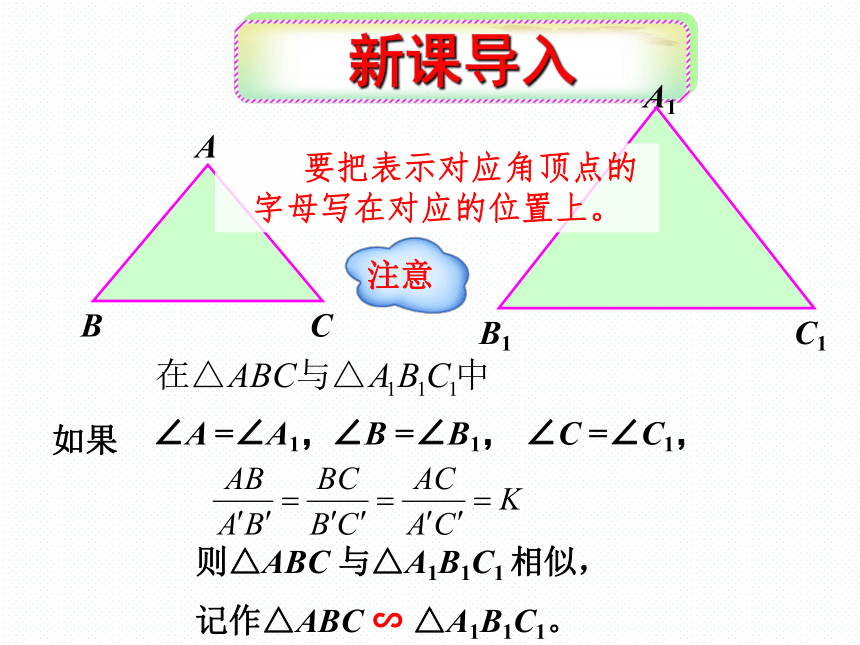
新课导入
A
B
C
A1
B1
C1
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1,
如果
则△ABC
与△A1B1C1
相似,
记作△ABC
∽
△A1B1C1。
要把表示对应角顶点的字母写在对应的位置上。
注意
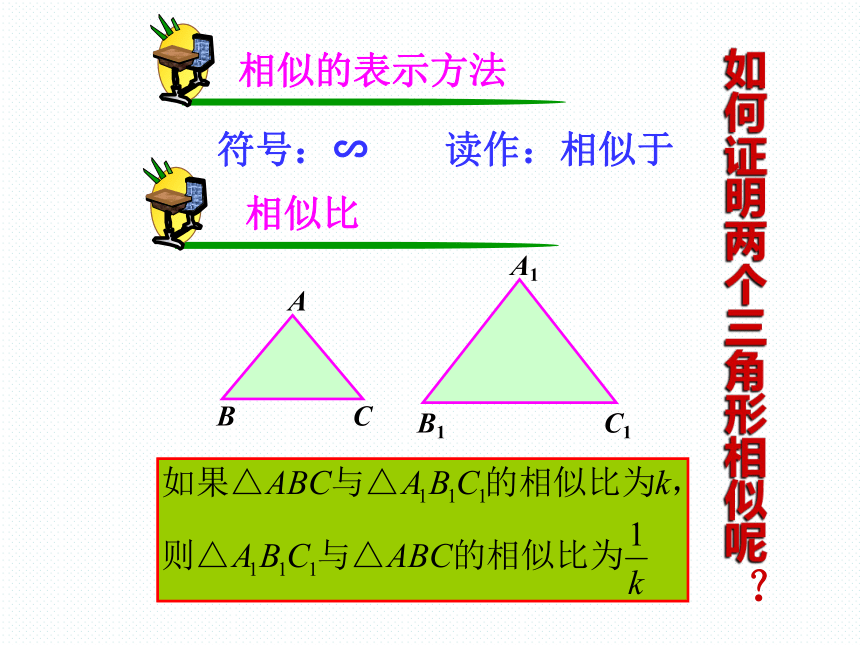
相似比
相似的表示方法
符号:∽
读作:相似于
A
B
C
A1
B1
C1
如何证明两个三角形相似呢?
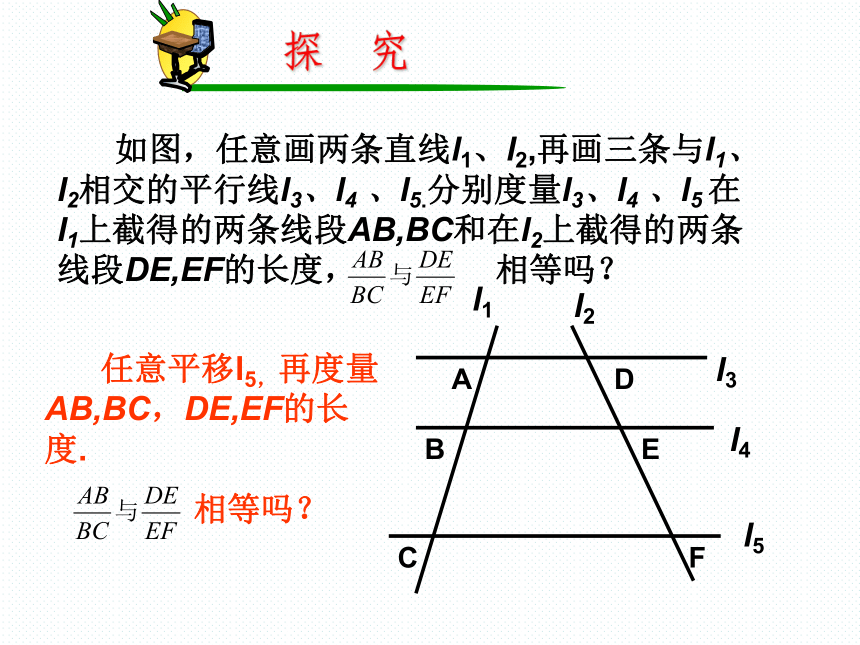
如图,任意画两条直线l1、l2,再画三条与l1、l2相交的平行线l3、l4
、l5.分别度量l3、l4
、l5
在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,
相等吗?
A
B
C
D
E
F
l1
l2
l3
l4
l5
任意平移l5,再度量AB,BC,DE,EF的长度.
相等吗?
探 究
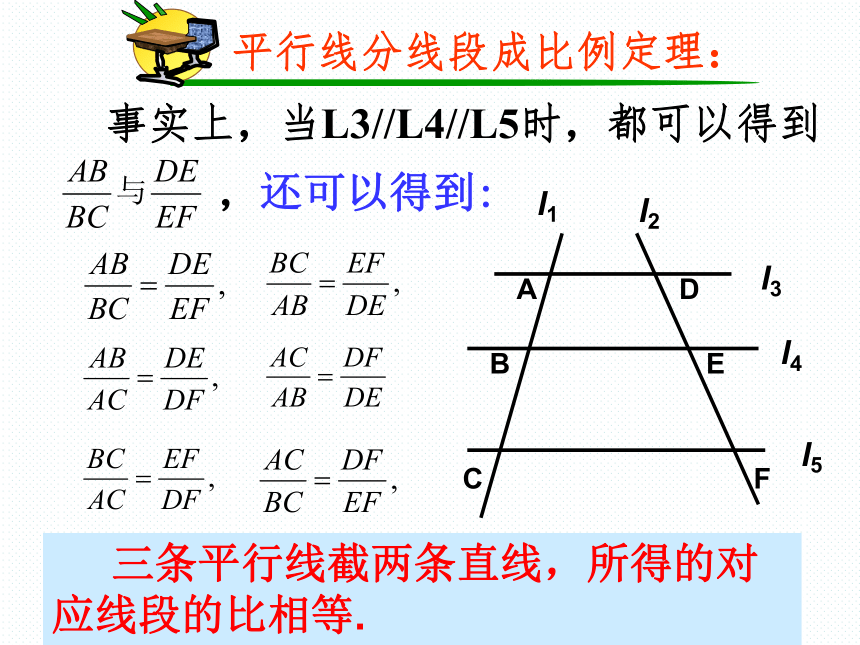
事实上,当L3//L4//L5时,都可以得到
,还可以得到:
平行线分线段成比例定理:
A
B
C
D
E
F
l1
l2
l3
l4
l5
三条平行线截两条直线,所得的对应线段的比相等.
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
A
B
C
D
E
l1
l2
l3
l4
l5
A
B
C
D
E
l1
l2
l3
l4
l5
已知:DE//BC,且D是边AB的中点,DE交AC于E
.
猜想:△ADE与△ABC有什么关系?并证明。
A
B
C
D
E
证明:
且
∠A=
∠A
∵
DE
//
BC
∴∠1
=∠B,∠2
=∠C
∴
△ADE与△ABC的对应角相等
相似。
1
2
三角形的中位线截得的三角形与原三角形相似,相似比
。
∴
四边形DBFE是平行四边形
∴
DE=BF
,
DB=
EF
∴
△ADE
∽
△ABC
A
B
C
D
E
F
过E作EF//AB交BC于F
又∵
DE
//
BC
又∵
AD
=
DB
∴
AD
=
EF
∵
∠A
=∠3,
∠2
=∠C
∴
△ADE≌△EFC
∴
DE
=
FC
=BF,
∴
∴
∴
△ADE与△ABC的对应边成比例
2
3
AE=EC
已知:DE//BC,△ADE与△ABC有什么关系?
猜想:△ADE与△ABC有什么关系?
相似。
A
B
C
D
E
F
当点D在AB上任意一点时,上面的结论还成立吗?
1
2
你能证明吗?
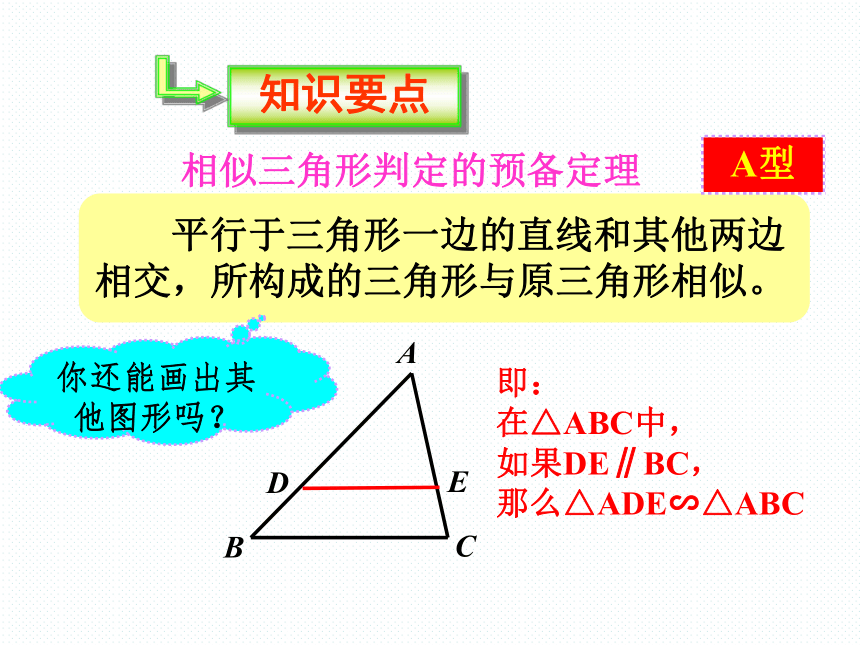
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
知识要点
相似三角形判定的预备定理
A
B
C
D
E
即:
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC
A型
你还能画出其他图形吗?
A
B
C
D
E
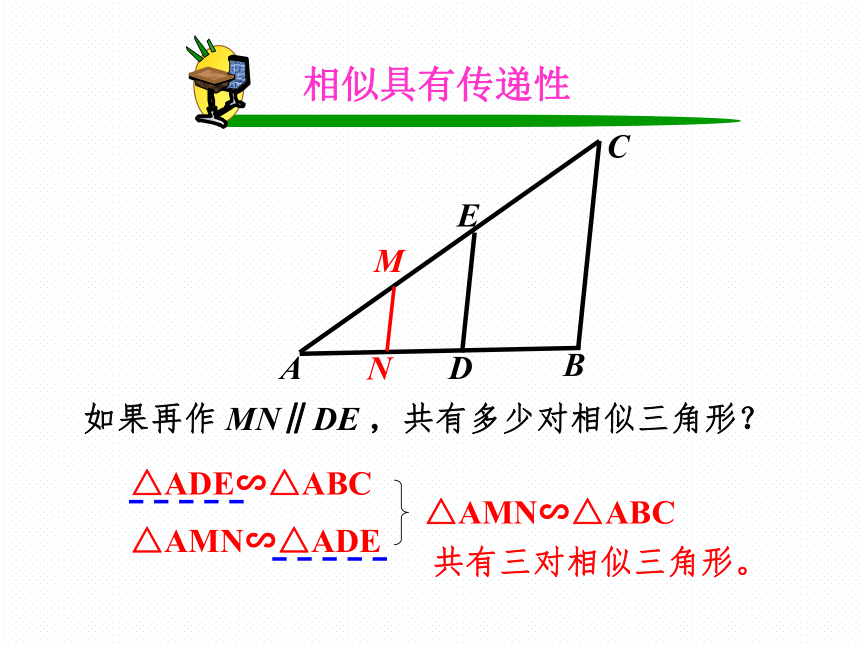
相似具有传递性
△ADE∽△ABC
M
N
如果再作
MN∥DE
,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形。
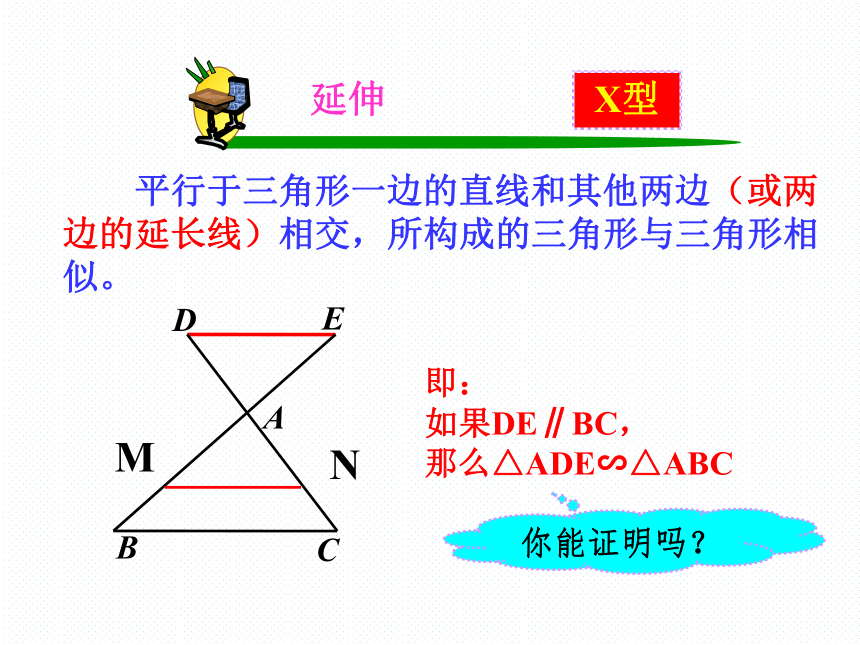
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
D
E
A
C
B
延伸
即:
如果DE∥BC,
那么△ADE∽△ABC
你能证明吗?
X型
M
N
平行于三角形一边的直线截其它两边,所得的对应线段成比例。
推论
A
B
C
D
E
即:
在△ABC中,
如果DE∥BC,
那么
(上比全,
全比上)
(上比下,下比上)
(下比全,全比下)
定义
判定方法
全等三角形
相似三角形
回顾并思考
三角、三边对应相等的两个三角形全等
三角对应相等,
三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边与直角边
H
L
判定三角形相似,是不是也有这么多种方法呢?
已知:
△ABC∽△A1B1C1.
A1
B1
C1
A
B
C
求证:
探究2
证明:在线段
(或它的延长线)上截取
,过点D作
,交
于点E根据前面的定理可得
.
A1
B1
C1
A
B
C
D
E
∴
又
A1
B1
C1
A
B
C
D
E
∴
∴
∴
(SSS)
∵
∴
如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
知识要点
判定三角形相似的定理之一
△ABC∽△A1B1C1.
即:
如果
那么
A1
B1
C1
A
B
C
三边对应成比例,两三角形相似。
边边边
S
S
S
√
求证:∠BAD=∠CAE。
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC
=∠DAE-∠DAC
即∠BAD=∠CAE
小练习
已知:
解:∵
边角边
S
A
S
探究2
已知:
△ABC∽△A1B1C1.
A1
B1
C1
A
B
C
求证:
∠B
=∠B1
.
你能证明吗?
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
知识要点
判定三角形相似的定理之二
两边对应成比例,且夹角相等,
两三角形相似。
边角边
S
A
S
√
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:
如果
∠B
=∠B1
.
那么
大家一起画一个三角形
,三个角分别为60°、45°、75°,大家画出的三角形相似吗?同桌的同学,通过测量对应边的长度进行比较。
探究3
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______。
相似
一定需要三个角吗?
角边角
A
S
A
角角边
A
A
S
角角
A
A
A1
B1
C1
A
B
C
已知:
△ABC∽△A1B1C1.
求证:
∠A
=∠A1,∠B
=∠B1
.
你能证明吗?
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
知识要点
判定三角形相似的定理之三
两角对应相等,两三角形相似。
角角
A
A
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:
如果
那么
√
∠A
=∠A1,∠B
=∠B1
.
如果两个三角形有一个内角对应相等,那么这两个三角形一定相似吗?
一角对应相等的两个三角形不一定相似。
△ACD
∽
△
CBD∽
△
ABC
小练习
找出图中所有的相似三角形。
射影定理图
B
D
A
C
有三对相似三角形:
△ACD∽
△CBD
△CBD∽
△ABC
△ACD∽
△ABC
常用的成比例的线段:
常用的相等的角:
∠A
=∠DCB
;∠B
=∠ACD
B
D
A
C
射影定理
例题
已知:DE∥BC,EF∥AB.
求证:△ADE∽△EFC.
A
E
F
B
C
D
解:
∵
DE∥BC,EF∥AB(已知)
∴∠ADE=∠B=∠EFC
(两直线平行,同位角相等)
∠AED=∠C(两直线平行,同位角相等)
∴
△ADE∽△EFC
(两个角分别对应相等的两个三角形相似)
相似三角形对应高的比等于相似比
∵△
ABC∽
△
A1B1C1
∴∠B
=
∠B1
又∵∠ADB
=
∠
A1D1B1
=900
∴△
ADB∽△
A1D1B1(角角)
A1
B1
C1
A
B
C
D
D1
证明:
∴
相似三角形对应角平分线的比等于相似比
∵
△
ABC∽
△
A1B1C1
∴
∠B
=
∠B1,∠BAC
=
∠B1A1C1
∵
AD,A1D1分别是∠BAC和∠B1A1C1的角平分线
∴
∠BAD
=
∠B1A1D1
∴
△
ADB∽△
A1D1B1(角角)
A1
B1
C1
A
B
C
D
D1
证明:
∴
相似三角形对应中线的比等于相似比
A1
B1
C1
A
B
C
D
D1
探究4
已知:
△ABC∽△A1B1C1.
求证:
你能证明吗?
H
L
A
B
C
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,
那么这两个直角三角形相似。
知识要点
判定三角形相似的定理之四
H
L
A
B
C
△ABC∽△A1B1C1.
即:
如果
那么
√
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
课堂小结
1.
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
三边对应成比例
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
对应角相等。
对应边成比例。
对应高的比等于相似比。
对应中线的比等于相似比。
对应角平分线的比等于相似比。
2.
相似三角形的性质:
(1)所有的等腰三角形都相似。
(2)所有的等腰直角三角形都相似。
(3)所有的等边三角形都相似。
(4)所有的直角三角形都相似。
(5)有一个角是100
°的两个等腰三角形都相似。
(6)有一个角是70
°的两个等腰三角形都相似。
(7)若两个三角形相似比为1,则它们必全等。
(8)相似的两个三角形一定大小不等。
1.
判断下列说法是否正确?并说明理由。
√
×
√
×
√
×
√
×
随堂练习
2.
AD⊥BC于点D,
CE⊥AB于点
E
,且交AD于F,你能从中找出几对相似三角形?
B
C
A
E
D
F
50°
30°
100°
30°
30°
3.
下面两组图形中的两个三角形是否相似?为什么?
A
C
B
A1
C1
B1
D
E
F
A
B
C
60°
相似
相似
4.
过△ABC(∠C>∠B)的边AB上一点D
作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?
C
D
●
A
B
B
C
A
D
E
E
B
C
A
D
△
ADE∽
△ABC
△
AED∽
△ABC
∠A=∠A
∠AED=∠C
∠A=∠A
∠AED=∠B
作DE,使∠AED=∠C
作DE,使∠AED=∠B
这样的直线有两条:
5.
已知:如图,AB∥EF
∥CD,图中共有___对相似三角形。
3
△EOF∽△COD
AB∥EF
△AOB∽
△FOE
AB∥CD
EF∥CD
△AOB
∽△DOC
6.
如果两个三角形的相似比为1,那么这两个三角形________。
7.
若△ABC与△A′B′C′相似,一组对应边的长为AB=3
cm,A′B′=4
cm,那么△A′B′C′与△ABC的相似比是________。
8.
若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么A′B′C′的最大边长是________。
全等
4︰3
24cm
9.
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
A
D
B
E
C
解:
(1)
∵
DE
∥
BC
∴
△ADE∽△ABC
∵∠AED
=∠C
=
400
在△ADE中,∠ADE
=180°-40°-45°=
95°
10.
已知:DE∥BC,AE=50cm,EC=30cm,
BC=70cm,∠BAC=45°,∠ACB=40°
求:(1)∠AED和∠ADE的大小。
(2)求DE的长。
(2)
∵△ADE∽△ABC
A
D
B
E
C
∴
新课导入
A
B
C
A1
B1
C1
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1,
如果
则△ABC
与△A1B1C1
相似,
记作△ABC
∽
△A1B1C1。
要把表示对应角顶点的字母写在对应的位置上。
注意
相似比
相似的表示方法
符号:∽
读作:相似于
A
B
C
A1
B1
C1
如何证明两个三角形相似呢?
如图,任意画两条直线l1、l2,再画三条与l1、l2相交的平行线l3、l4
、l5.分别度量l3、l4
、l5
在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,
相等吗?
A
B
C
D
E
F
l1
l2
l3
l4
l5
任意平移l5,再度量AB,BC,DE,EF的长度.
相等吗?
探 究
事实上,当L3//L4//L5时,都可以得到
,还可以得到:
平行线分线段成比例定理:
A
B
C
D
E
F
l1
l2
l3
l4
l5
三条平行线截两条直线,所得的对应线段的比相等.
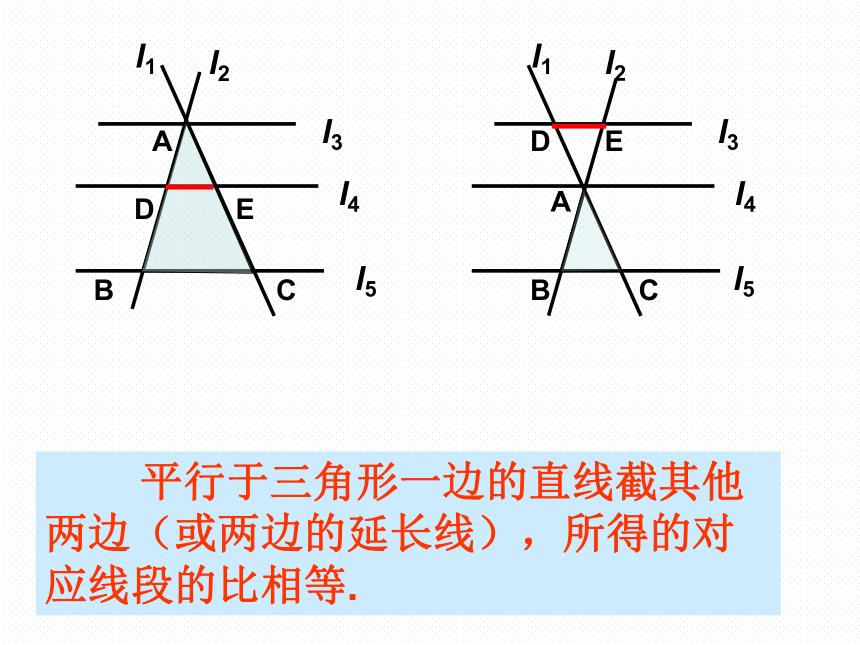
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
A
B
C
D
E
l1
l2
l3
l4
l5
A
B
C
D
E
l1
l2
l3
l4
l5
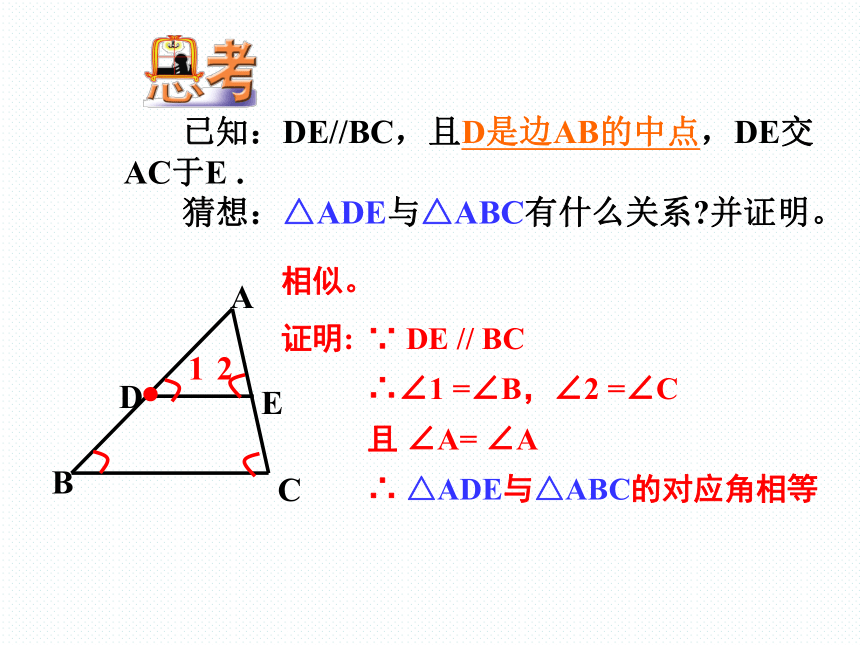
已知:DE//BC,且D是边AB的中点,DE交AC于E
.
猜想:△ADE与△ABC有什么关系?并证明。
A
B
C
D
E
证明:
且
∠A=
∠A
∵
DE
//
BC
∴∠1
=∠B,∠2
=∠C
∴
△ADE与△ABC的对应角相等
相似。
1
2
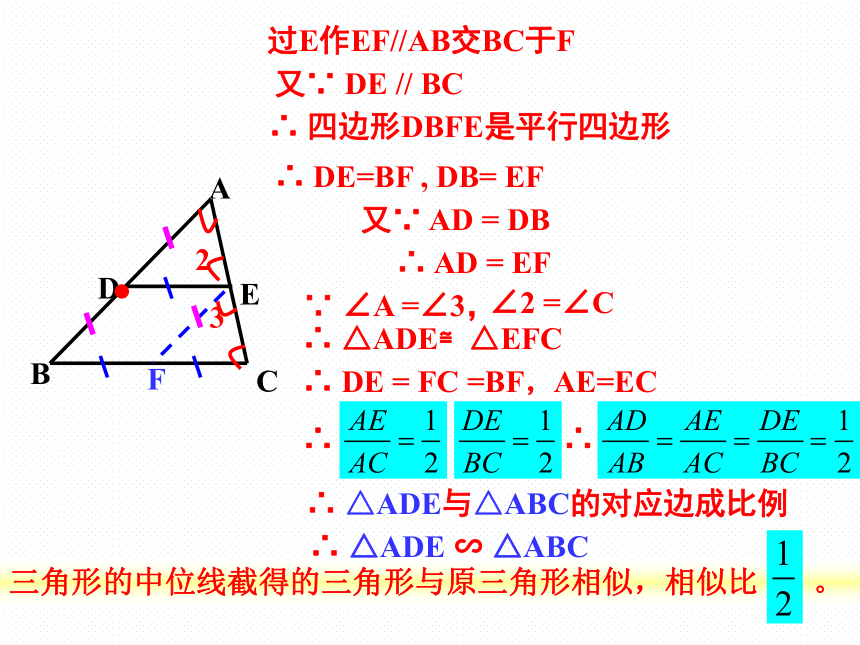
三角形的中位线截得的三角形与原三角形相似,相似比
。
∴
四边形DBFE是平行四边形
∴
DE=BF
,
DB=
EF
∴
△ADE
∽
△ABC
A
B
C
D
E
F
过E作EF//AB交BC于F
又∵
DE
//
BC
又∵
AD
=
DB
∴
AD
=
EF
∵
∠A
=∠3,
∠2
=∠C
∴
△ADE≌△EFC
∴
DE
=
FC
=BF,
∴
∴
∴
△ADE与△ABC的对应边成比例
2
3
AE=EC
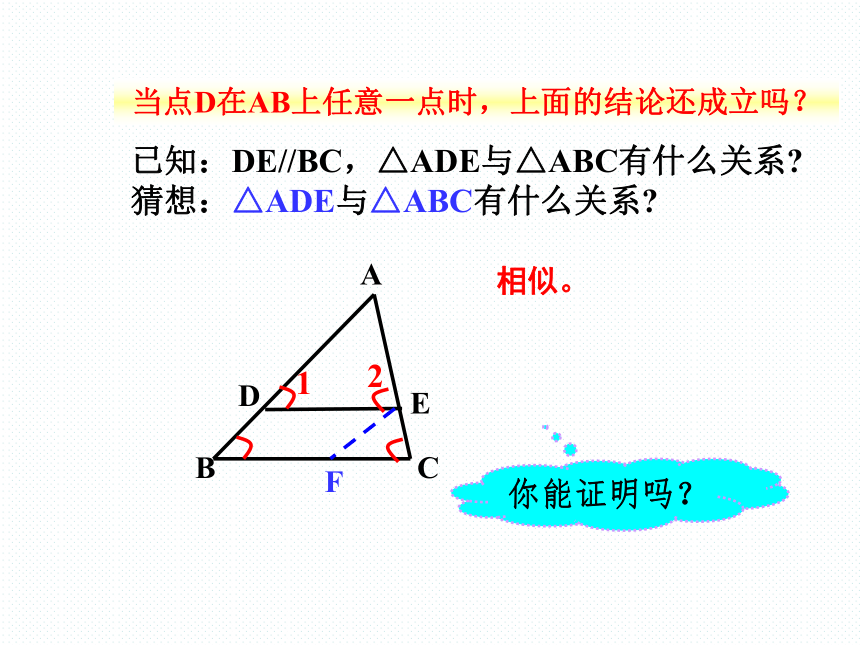
已知:DE//BC,△ADE与△ABC有什么关系?
猜想:△ADE与△ABC有什么关系?
相似。
A
B
C
D
E
F
当点D在AB上任意一点时,上面的结论还成立吗?
1
2
你能证明吗?
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
知识要点
相似三角形判定的预备定理
A
B
C
D
E
即:
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC
A型
你还能画出其他图形吗?
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
M
N
如果再作
MN∥DE
,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形。
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
D
E
A
C
B
延伸
即:
如果DE∥BC,
那么△ADE∽△ABC
你能证明吗?
X型
M
N
平行于三角形一边的直线截其它两边,所得的对应线段成比例。
推论
A
B
C
D
E
即:
在△ABC中,
如果DE∥BC,
那么
(上比全,
全比上)
(上比下,下比上)
(下比全,全比下)
定义
判定方法
全等三角形
相似三角形
回顾并思考
三角、三边对应相等的两个三角形全等
三角对应相等,
三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边与直角边
H
L
判定三角形相似,是不是也有这么多种方法呢?
已知:
△ABC∽△A1B1C1.
A1
B1
C1
A
B
C
求证:
探究2
证明:在线段
(或它的延长线)上截取
,过点D作
,交
于点E根据前面的定理可得
.
A1
B1
C1
A
B
C
D
E
∴
又
A1
B1
C1
A
B
C
D
E
∴
∴
∴
(SSS)
∵
∴
如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
知识要点
判定三角形相似的定理之一
△ABC∽△A1B1C1.
即:
如果
那么
A1
B1
C1
A
B
C
三边对应成比例,两三角形相似。
边边边
S
S
S
√
求证:∠BAD=∠CAE。
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC
=∠DAE-∠DAC
即∠BAD=∠CAE
小练习
已知:
解:∵
边角边
S
A
S
探究2
已知:
△ABC∽△A1B1C1.
A1
B1
C1
A
B
C
求证:
∠B
=∠B1
.
你能证明吗?
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
知识要点
判定三角形相似的定理之二
两边对应成比例,且夹角相等,
两三角形相似。
边角边
S
A
S
√
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:
如果
∠B
=∠B1
.
那么
大家一起画一个三角形
,三个角分别为60°、45°、75°,大家画出的三角形相似吗?同桌的同学,通过测量对应边的长度进行比较。
探究3
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______。
相似
一定需要三个角吗?
角边角
A
S
A
角角边
A
A
S
角角
A
A
A1
B1
C1
A
B
C
已知:
△ABC∽△A1B1C1.
求证:
∠A
=∠A1,∠B
=∠B1
.
你能证明吗?
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
知识要点
判定三角形相似的定理之三
两角对应相等,两三角形相似。
角角
A
A
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:
如果
那么
√
∠A
=∠A1,∠B
=∠B1
.
如果两个三角形有一个内角对应相等,那么这两个三角形一定相似吗?
一角对应相等的两个三角形不一定相似。
△ACD
∽
△
CBD∽
△
ABC
小练习
找出图中所有的相似三角形。
射影定理图
B
D
A
C
有三对相似三角形:
△ACD∽
△CBD
△CBD∽
△ABC
△ACD∽
△ABC
常用的成比例的线段:
常用的相等的角:
∠A
=∠DCB
;∠B
=∠ACD
B
D
A
C
射影定理
例题
已知:DE∥BC,EF∥AB.
求证:△ADE∽△EFC.
A
E
F
B
C
D
解:
∵
DE∥BC,EF∥AB(已知)
∴∠ADE=∠B=∠EFC
(两直线平行,同位角相等)
∠AED=∠C(两直线平行,同位角相等)
∴
△ADE∽△EFC
(两个角分别对应相等的两个三角形相似)
相似三角形对应高的比等于相似比
∵△
ABC∽
△
A1B1C1
∴∠B
=
∠B1
又∵∠ADB
=
∠
A1D1B1
=900
∴△
ADB∽△
A1D1B1(角角)
A1
B1
C1
A
B
C
D
D1
证明:
∴
相似三角形对应角平分线的比等于相似比
∵
△
ABC∽
△
A1B1C1
∴
∠B
=
∠B1,∠BAC
=
∠B1A1C1
∵
AD,A1D1分别是∠BAC和∠B1A1C1的角平分线
∴
∠BAD
=
∠B1A1D1
∴
△
ADB∽△
A1D1B1(角角)
A1
B1
C1
A
B
C
D
D1
证明:
∴
相似三角形对应中线的比等于相似比
A1
B1
C1
A
B
C
D
D1
探究4
已知:
△ABC∽△A1B1C1.
求证:
你能证明吗?
H
L
A
B
C
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,
那么这两个直角三角形相似。
知识要点
判定三角形相似的定理之四
H
L
A
B
C
△ABC∽△A1B1C1.
即:
如果
那么
√
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
课堂小结
1.
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
三边对应成比例
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
对应角相等。
对应边成比例。
对应高的比等于相似比。
对应中线的比等于相似比。
对应角平分线的比等于相似比。
2.
相似三角形的性质:
(1)所有的等腰三角形都相似。
(2)所有的等腰直角三角形都相似。
(3)所有的等边三角形都相似。
(4)所有的直角三角形都相似。
(5)有一个角是100
°的两个等腰三角形都相似。
(6)有一个角是70
°的两个等腰三角形都相似。
(7)若两个三角形相似比为1,则它们必全等。
(8)相似的两个三角形一定大小不等。
1.
判断下列说法是否正确?并说明理由。
√
×
√
×
√
×
√
×
随堂练习
2.
AD⊥BC于点D,
CE⊥AB于点
E
,且交AD于F,你能从中找出几对相似三角形?
B
C
A
E
D
F
50°
30°
100°
30°
30°
3.
下面两组图形中的两个三角形是否相似?为什么?
A
C
B
A1
C1
B1
D
E
F
A
B
C
60°
相似
相似
4.
过△ABC(∠C>∠B)的边AB上一点D
作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?
C
D
●
A
B
B
C
A
D
E
E
B
C
A
D
△
ADE∽
△ABC
△
AED∽
△ABC
∠A=∠A
∠AED=∠C
∠A=∠A
∠AED=∠B
作DE,使∠AED=∠C
作DE,使∠AED=∠B
这样的直线有两条:
5.
已知:如图,AB∥EF
∥CD,图中共有___对相似三角形。
3
△EOF∽△COD
AB∥EF
△AOB∽
△FOE
AB∥CD
EF∥CD
△AOB
∽△DOC
6.
如果两个三角形的相似比为1,那么这两个三角形________。
7.
若△ABC与△A′B′C′相似,一组对应边的长为AB=3
cm,A′B′=4
cm,那么△A′B′C′与△ABC的相似比是________。
8.
若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么A′B′C′的最大边长是________。
全等
4︰3
24cm
9.
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
A
D
B
E
C
解:
(1)
∵
DE
∥
BC
∴
△ADE∽△ABC
∵∠AED
=∠C
=
400
在△ADE中,∠ADE
=180°-40°-45°=
95°
10.
已知:DE∥BC,AE=50cm,EC=30cm,
BC=70cm,∠BAC=45°,∠ACB=40°
求:(1)∠AED和∠ADE的大小。
(2)求DE的长。
(2)
∵△ADE∽△ABC
A
D
B
E
C
∴
