1.1.2 菱形的性质与判定 课件(共17张PPT)
文档属性
| 名称 | 1.1.2 菱形的性质与判定 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
数学北师大版
九年级
第一章
特殊平行四边形
1
菱形的性质与判定
第2课时
菱形的性质与判定(二)
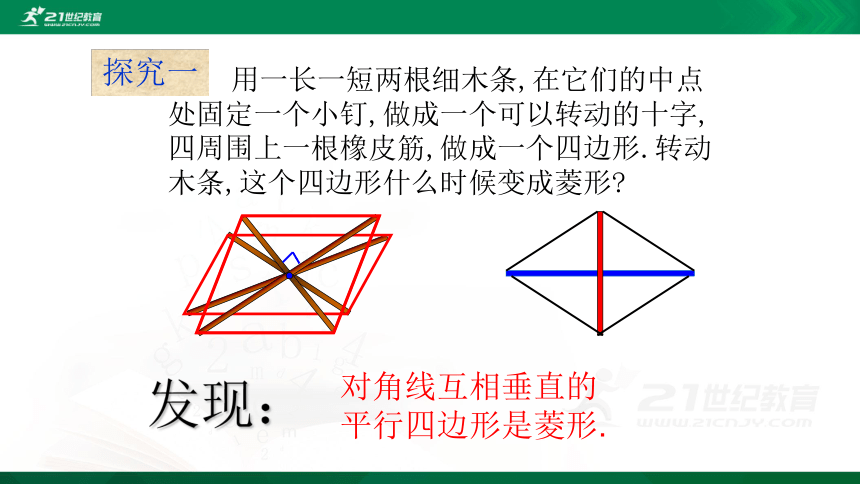
探究一
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
发现:
对角线互相垂直的平行四边形是菱形.
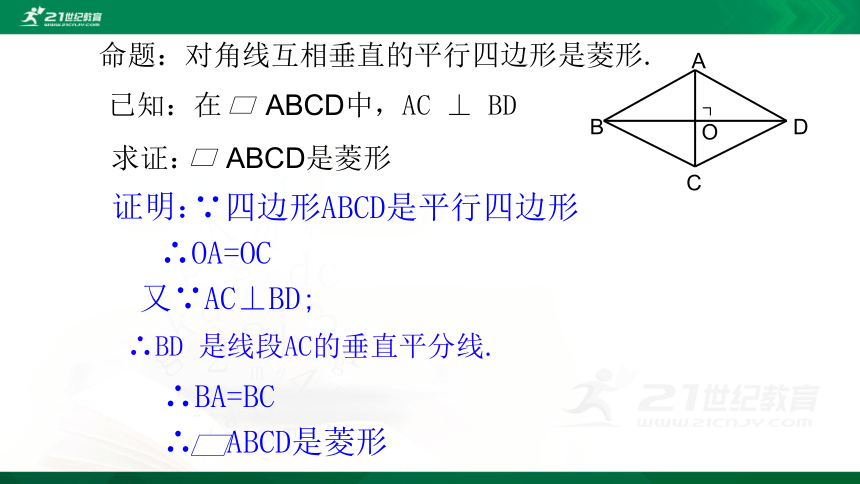
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴
ABCD是菱形
已知:在
ABCD中,AC
⊥
BD
求证:
ABCD是菱形
∴BD
是线段AC的垂直平分线.
A
B
C
D
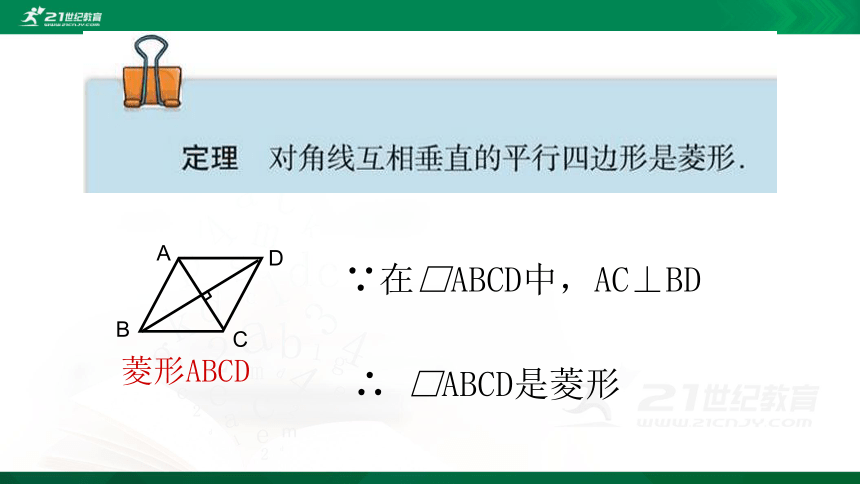
菱形ABCD
∵在□ABCD中,AC⊥BD
∴
□ABCD是菱形
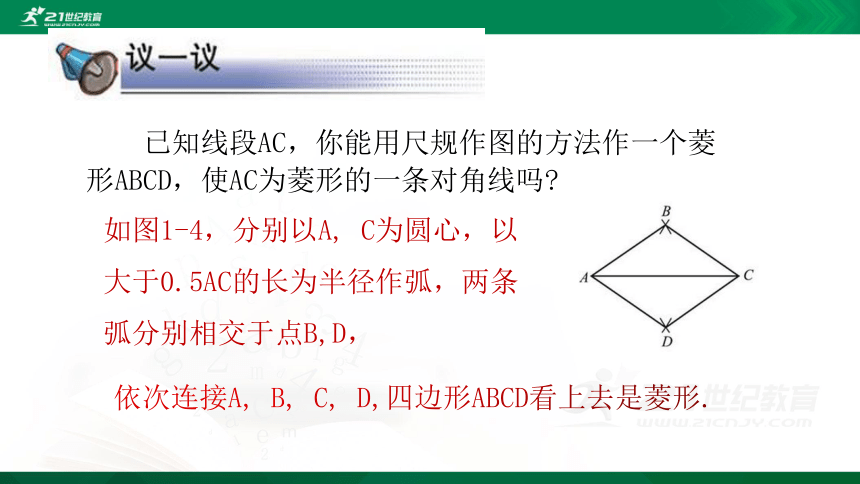
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
如图1-4,分别以A,
C为圆心,以大于0.5AC的长为半径作弧,两条弧分别相交于点B,D,
依次连接A,
B,
C,
D,四边形ABCD看上去是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
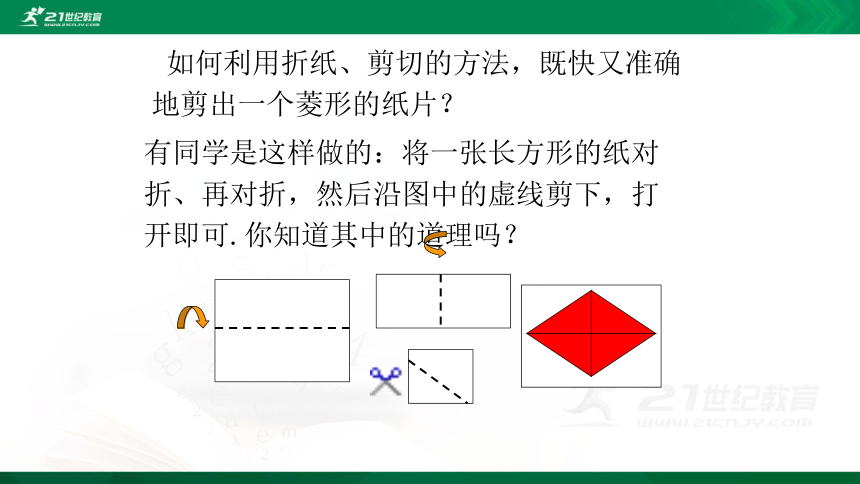
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
证明:在△AOB中,
∴AB2=OA2+OB2
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD
∴□ABCD是菱形
(对角线垂直的平行四边形是菱形)
∵
AB=
√5,OA=2,OB=1
例2已知:如图1-6,在口ABCD中,对角线AC与BD交于点O.AB=
,OA=2,OB=1.求证:口ABCD是菱形
练习、已知:如图,AD平分∠BAC,DE∥AC
交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴
□AEDF是菱形
证明:∵DE∥AC
DF∥AB
∴四边形AEDF是平行四边形
∵
DE∥AC
∴∠2=∠3
∵
AD是△ABC的角平分线
∴AE=DE
∴
∠1=∠3
∴
∠1=∠2
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
+邻边相等
=
+对角线线互相垂直=
四条边相等+
=
归纳:
作业布置:
习题1.1
1,2,3,4
选讲内容:
1、如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
H
G
F
E
D
C
B
A
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
2、如图,
ABCD的两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6
求证:四边形ABCD是菱形.
A
B
C
D
O
∴平行四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
在三角形AOB中
∴AC⊥BD
∴∠AOB=90°
∵
四边形ABCD是平行四边形
∴AB2=AO2+BO2
又∵AB=5
3、已知:如图,□
ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
∟
∵EF垂直平分AC
∴AO=CO,
∠AOE=90°
∴∠FOC=∠AOE=90°
∵四边形ABCD是平行四边形
∴
AD∥BC
∴AE∥FC
∴∠AEO=∠CFO
∴△AEO≌△CFO
证明:
∴OE=OF
又∵AO=CO
∴四边形AFCE是平行四边形
又∵EF⊥AC
∴四边形AFCE是菱形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
九年级
第一章
特殊平行四边形
1
菱形的性质与判定
第2课时
菱形的性质与判定(二)
探究一
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
发现:
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴
ABCD是菱形
已知:在
ABCD中,AC
⊥
BD
求证:
ABCD是菱形
∴BD
是线段AC的垂直平分线.
A
B
C
D
菱形ABCD
∵在□ABCD中,AC⊥BD
∴
□ABCD是菱形
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
如图1-4,分别以A,
C为圆心,以大于0.5AC的长为半径作弧,两条弧分别相交于点B,D,
依次连接A,
B,
C,
D,四边形ABCD看上去是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
证明:在△AOB中,
∴AB2=OA2+OB2
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD
∴□ABCD是菱形
(对角线垂直的平行四边形是菱形)
∵
AB=
√5,OA=2,OB=1
例2已知:如图1-6,在口ABCD中,对角线AC与BD交于点O.AB=
,OA=2,OB=1.求证:口ABCD是菱形
练习、已知:如图,AD平分∠BAC,DE∥AC
交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴
□AEDF是菱形
证明:∵DE∥AC
DF∥AB
∴四边形AEDF是平行四边形
∵
DE∥AC
∴∠2=∠3
∵
AD是△ABC的角平分线
∴AE=DE
∴
∠1=∠3
∴
∠1=∠2
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
+邻边相等
=
+对角线线互相垂直=
四条边相等+
=
归纳:
作业布置:
习题1.1
1,2,3,4
选讲内容:
1、如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
H
G
F
E
D
C
B
A
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
2、如图,
ABCD的两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6
求证:四边形ABCD是菱形.
A
B
C
D
O
∴平行四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
在三角形AOB中
∴AC⊥BD
∴∠AOB=90°
∵
四边形ABCD是平行四边形
∴AB2=AO2+BO2
又∵AB=5
3、已知:如图,□
ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
∟
∵EF垂直平分AC
∴AO=CO,
∠AOE=90°
∴∠FOC=∠AOE=90°
∵四边形ABCD是平行四边形
∴
AD∥BC
∴AE∥FC
∴∠AEO=∠CFO
∴△AEO≌△CFO
证明:
∴OE=OF
又∵AO=CO
∴四边形AFCE是平行四边形
又∵EF⊥AC
∴四边形AFCE是菱形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
