1.3.2 正方形的性质与判定 课件(共27张PPT)
文档属性
| 名称 | 1.3.2 正方形的性质与判定 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 22:10:17 | ||
图片预览








文档简介
(共27张PPT)
数学北师大版
九年级
1.3
正方形的性质与判定
第2课时
正方形的判定
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
温故知新
三角形中位线性质:
平行且等于底边的一半
动一动:过点A作射线AM的垂线AN,分别在AM
,
AN上取点B
,
D
,使,作DC∥AB
,
BC∥AD
,得四边形ABCD.
A
M
N
B
D
C
问题1:上面所画四边形ABCD是正方形吗?为什么?
∵DC∥AB
,
BC∥AD
四边形ABCD是正方形
四边形ABCD是平行四边开
AM⊥AN
AB=AD
依据定义可知:四边形ABCD是正方形
想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形展开后是个正方形?
使两直角边相等AB=AC
A
C
B
问题1:满足怎样条件的矩形是正方形?
问题2:满足怎样条件的菱形是正方形?
①依据正方形可知定义:一组邻边相等的矩形
②对角线互相垂直的矩形
①依据正方形可知定义:有一个角是直角的菱形
②对角线互相平分的菱形
定理:对角线相等的菱形是正方形.
定理:对角线垂直的矩形是正方形.
定理:有一个角是直角的菱形是正方形.
定理:有一组邻边相等的矩形是正方形.
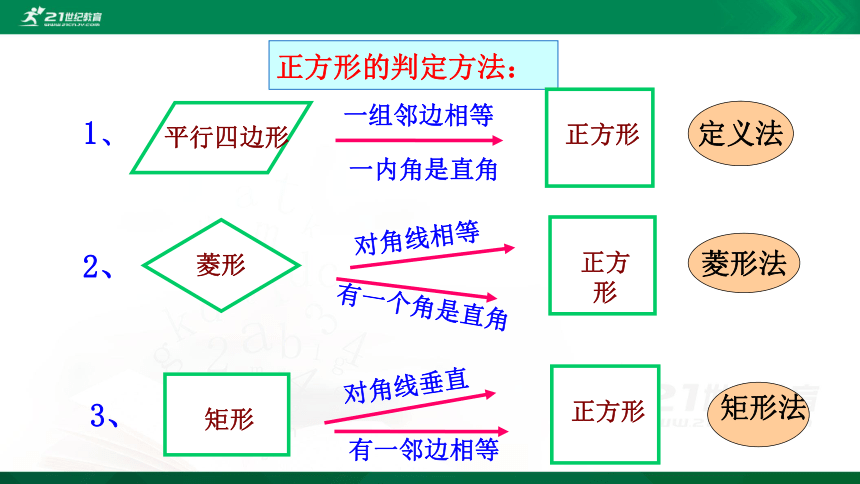
正方形的判定方法:
1、
平行四边形
一组邻边相等
一内角是直角
正方形
定义法
2、
菱形
有一个角是直角
对角线相等
正方形
菱形法
3、
矩形
对角线垂直
正方形
矩形法
有一邻边相等
1.正方形的一条对角线把正方形分成两个全等的等腰直角三角形(
)
2.对角线互相垂直且相等的四边形是正方形(
)
3.如果一个菱形的对角线相等,那么它一定
是正方形
(
)
4.如果一个矩形的对角线互相垂直,那么它
一定是正方形
(
)
5.四条边相等,且有一个角是直角的四边形
是正方形(
)
√
√
√
×
√
判断题
6.正方形一定是矩形.(
)
7.正方形一定是菱形.(
)
8.菱形一定是正方形.(
)
9.矩形一定是正方形.(
)
10.正方形、矩形、菱形都是平行四边形.
(
)
√
√
√
×
×
11.正方形是轴对称图形,一共有2条对称轴(
)
12.四个角都相等的四边形是正方形
(
)
13.四条边都相等的四边形是正方形
(
)
×
×
×
例1:如图,在矩形ABCD中,
BE平分∠ABC
,
CE平分∠DCB
,
BF∥CE
,
CF∥BE.
求证:四边形BECF是正方形.
证明:
∵
BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴
∠ABC
=
90°,
∠DCB
=
90°,
∵BE平分∠ABC,
CE平分∠
DCB,
∴∠EBC
=
45°,
∠ECB
=
45°,
∴
∠
EBC
=∠
ECB
.
∴
EB=EC,∴□
BECF是菱形
.
在△EBC中
∵
∠EBC
=
45°,∠ECB
=
45°,
∴∠BEC
=
90°,
∴菱形BECF是正方形.
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形、菱形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
平行四边形
A
B
C
D
菱形
A
B
C
D
正方形
矩形
以四边形各边中点为顶点所组成的新四边形的形状与哪些线段有关系?有怎样的关系?
以四边形的二条对角线有关系,
依据是三角形中位线性质:平行且等于底边的一半。
新的四边形的每一边都平行且等于一条对角线的一半。
例2:如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO
=45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO
≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
B
O
E
H
G
F
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO
,即EG=HF,
∴四边形EFGH为正方形.
例3.如图,在四边形ABCD中,
AB=BC
,对角线BD平分?ABC
,
P是BD上一点,过点P作PM?AD
,
PN?CD
,垂足分别为M、N.
(1)
求证:?ADB=?CDB;
(2)
若?ADC=90?,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(AAS).
∴∠ADB=∠CDB.
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形(有一组邻边相等的矩形是正方形).
C
A
B
D
P
M
N
正方形的判定方法:
1、
平行四边形
一组邻边相等
一内角是直角
正方形
定义法
2、
菱形
有一个角是直角
对角线相等
正方形
菱形法
3、
矩形
对角线垂直
正方形
矩形法
有一邻边相等
作业布置:
习题1.8
1,2,3,4
选讲内容:
1.将五个边长都为2
cm的正方形按如图1-3-7所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为?( )
提示如图,连接AP,AN,点A是正方形MNPQ的中心,则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积.
4
2.如图,在矩形ABCD中,M、N分别是AD、BC的中点,E、F分别是边
BM、CM的中点,当AB∶AD= ????时,四边形MENF是正方形.
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形.
解析 当AB∶AD=1∶2时,四边形MENF是正方形.
∵AB∶AD=1∶2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠BMC=90°.
∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,∴BM=CM.
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF=ME=MF,NF∥BM,NE∥CM,
3.如图,正方形ABCD的边长为2,点E、F分别在边
AD、CD上,若∠EBF=45°,则△EDF的周长等于 ????.
解析????将△BCF绕点B逆时针旋转90°到△BAC'的位置,
∵∠BAC'+∠BAD=180°,
∵∠ABC=90°,∠EBF=45°,
∵∠FBC=∠C'BA,
∴EF=EA+AC'=EA+FC,
∴△DEF的周长=DE+DF+EF=DA+DC=4.
∴C'、A、D三点共线.
∴∠FBC+∠EBA=45°.
∴∠C'BA+∠EBA=45°,
∴∠EBF=∠EBC'=45°.
在△EBF和△EBC'中,?
∴△EBF≌△EBC',∴EF=EC',
又CF=AC',
4.如图1-3-8①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C、D不重合),以CG为边在正方形ABCD外作正方形CEFG,连接BG、DE.我们探究图1-3-8中线段BG、线段DE的长度关系及所在直线的位置关系.
(1)猜想图1-3-8①中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图1-3-8①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图1-3-8②、1-3-8③的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图1-3-8②证明你的判断.
解析 (1)BG=DE,BG⊥DE.
(2)BG=DE,BG⊥DE仍然成立.
证明:设BG与DE相交于点O,
因为四边形ABCD、四边形CEFG都是正方形,
所以BC=CD,CG=CE,∠BCD=∠ECG=90°.
所以∠BCG=∠DCE.
所以△BCG≌△DCE.
所以BG=DE,∠CBG=∠CDE.
又因为∠BHC=∠DHO,∠CBG+∠BHC=90°,
所以∠CDE+∠DHO=90°,
所以∠DOH=90°.
5.如图①所示,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图②所示,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图③所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
解析 (1)BM=FN.
证明:因为△GEF是等腰直角三角形,四边形ABCD是正方形,
所以∠ABD=∠F=45°,OB=OF.
又因为∠BOM=∠FON,
所以△OBM≌△OFN,所以BM=FN.
(2)BM=FN仍然成立.
证明:因为△GEF是等腰直角三角形,四边形ABCD是正方形,所以
∠DBA=∠GFE=45°,OB=OF.
所以∠MBO=∠NFO=135°.
又因为∠MOB=∠NOF,所以△OBM≌△OFN,
所以BM=FN.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
九年级
1.3
正方形的性质与判定
第2课时
正方形的判定
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
温故知新
三角形中位线性质:
平行且等于底边的一半
动一动:过点A作射线AM的垂线AN,分别在AM
,
AN上取点B
,
D
,使,作DC∥AB
,
BC∥AD
,得四边形ABCD.
A
M
N
B
D
C
问题1:上面所画四边形ABCD是正方形吗?为什么?
∵DC∥AB
,
BC∥AD
四边形ABCD是正方形
四边形ABCD是平行四边开
AM⊥AN
AB=AD
依据定义可知:四边形ABCD是正方形
想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形展开后是个正方形?
使两直角边相等AB=AC
A
C
B
问题1:满足怎样条件的矩形是正方形?
问题2:满足怎样条件的菱形是正方形?
①依据正方形可知定义:一组邻边相等的矩形
②对角线互相垂直的矩形
①依据正方形可知定义:有一个角是直角的菱形
②对角线互相平分的菱形
定理:对角线相等的菱形是正方形.
定理:对角线垂直的矩形是正方形.
定理:有一个角是直角的菱形是正方形.
定理:有一组邻边相等的矩形是正方形.
正方形的判定方法:
1、
平行四边形
一组邻边相等
一内角是直角
正方形
定义法
2、
菱形
有一个角是直角
对角线相等
正方形
菱形法
3、
矩形
对角线垂直
正方形
矩形法
有一邻边相等
1.正方形的一条对角线把正方形分成两个全等的等腰直角三角形(
)
2.对角线互相垂直且相等的四边形是正方形(
)
3.如果一个菱形的对角线相等,那么它一定
是正方形
(
)
4.如果一个矩形的对角线互相垂直,那么它
一定是正方形
(
)
5.四条边相等,且有一个角是直角的四边形
是正方形(
)
√
√
√
×
√
判断题
6.正方形一定是矩形.(
)
7.正方形一定是菱形.(
)
8.菱形一定是正方形.(
)
9.矩形一定是正方形.(
)
10.正方形、矩形、菱形都是平行四边形.
(
)
√
√
√
×
×
11.正方形是轴对称图形,一共有2条对称轴(
)
12.四个角都相等的四边形是正方形
(
)
13.四条边都相等的四边形是正方形
(
)
×
×
×
例1:如图,在矩形ABCD中,
BE平分∠ABC
,
CE平分∠DCB
,
BF∥CE
,
CF∥BE.
求证:四边形BECF是正方形.
证明:
∵
BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴
∠ABC
=
90°,
∠DCB
=
90°,
∵BE平分∠ABC,
CE平分∠
DCB,
∴∠EBC
=
45°,
∠ECB
=
45°,
∴
∠
EBC
=∠
ECB
.
∴
EB=EC,∴□
BECF是菱形
.
在△EBC中
∵
∠EBC
=
45°,∠ECB
=
45°,
∴∠BEC
=
90°,
∴菱形BECF是正方形.
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形、菱形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
平行四边形
A
B
C
D
菱形
A
B
C
D
正方形
矩形
以四边形各边中点为顶点所组成的新四边形的形状与哪些线段有关系?有怎样的关系?
以四边形的二条对角线有关系,
依据是三角形中位线性质:平行且等于底边的一半。
新的四边形的每一边都平行且等于一条对角线的一半。
例2:如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO
=45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO
≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
B
O
E
H
G
F
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO
,即EG=HF,
∴四边形EFGH为正方形.
例3.如图,在四边形ABCD中,
AB=BC
,对角线BD平分?ABC
,
P是BD上一点,过点P作PM?AD
,
PN?CD
,垂足分别为M、N.
(1)
求证:?ADB=?CDB;
(2)
若?ADC=90?,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(AAS).
∴∠ADB=∠CDB.
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形(有一组邻边相等的矩形是正方形).
C
A
B
D
P
M
N
正方形的判定方法:
1、
平行四边形
一组邻边相等
一内角是直角
正方形
定义法
2、
菱形
有一个角是直角
对角线相等
正方形
菱形法
3、
矩形
对角线垂直
正方形
矩形法
有一邻边相等
作业布置:
习题1.8
1,2,3,4
选讲内容:
1.将五个边长都为2
cm的正方形按如图1-3-7所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为?( )
提示如图,连接AP,AN,点A是正方形MNPQ的中心,则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积.
4
2.如图,在矩形ABCD中,M、N分别是AD、BC的中点,E、F分别是边
BM、CM的中点,当AB∶AD= ????时,四边形MENF是正方形.
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形.
解析 当AB∶AD=1∶2时,四边形MENF是正方形.
∵AB∶AD=1∶2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠BMC=90°.
∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,∴BM=CM.
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF=ME=MF,NF∥BM,NE∥CM,
3.如图,正方形ABCD的边长为2,点E、F分别在边
AD、CD上,若∠EBF=45°,则△EDF的周长等于 ????.
解析????将△BCF绕点B逆时针旋转90°到△BAC'的位置,
∵∠BAC'+∠BAD=180°,
∵∠ABC=90°,∠EBF=45°,
∵∠FBC=∠C'BA,
∴EF=EA+AC'=EA+FC,
∴△DEF的周长=DE+DF+EF=DA+DC=4.
∴C'、A、D三点共线.
∴∠FBC+∠EBA=45°.
∴∠C'BA+∠EBA=45°,
∴∠EBF=∠EBC'=45°.
在△EBF和△EBC'中,?
∴△EBF≌△EBC',∴EF=EC',
又CF=AC',
4.如图1-3-8①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C、D不重合),以CG为边在正方形ABCD外作正方形CEFG,连接BG、DE.我们探究图1-3-8中线段BG、线段DE的长度关系及所在直线的位置关系.
(1)猜想图1-3-8①中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图1-3-8①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图1-3-8②、1-3-8③的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图1-3-8②证明你的判断.
解析 (1)BG=DE,BG⊥DE.
(2)BG=DE,BG⊥DE仍然成立.
证明:设BG与DE相交于点O,
因为四边形ABCD、四边形CEFG都是正方形,
所以BC=CD,CG=CE,∠BCD=∠ECG=90°.
所以∠BCG=∠DCE.
所以△BCG≌△DCE.
所以BG=DE,∠CBG=∠CDE.
又因为∠BHC=∠DHO,∠CBG+∠BHC=90°,
所以∠CDE+∠DHO=90°,
所以∠DOH=90°.
5.如图①所示,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图②所示,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图③所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
解析 (1)BM=FN.
证明:因为△GEF是等腰直角三角形,四边形ABCD是正方形,
所以∠ABD=∠F=45°,OB=OF.
又因为∠BOM=∠FON,
所以△OBM≌△OFN,所以BM=FN.
(2)BM=FN仍然成立.
证明:因为△GEF是等腰直角三角形,四边形ABCD是正方形,所以
∠DBA=∠GFE=45°,OB=OF.
所以∠MBO=∠NFO=135°.
又因为∠MOB=∠NOF,所以△OBM≌△OFN,
所以BM=FN.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
