人教版六年级上册第五章5.2圆的面积同步学案
文档属性
| 名称 | 人教版六年级上册第五章5.2圆的面积同步学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 19:56:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二讲 圆的面积
【知识巩固】
圆面积:
圆环的面积为:
扇形的面积为:
半圆面积:,90°扇形面积
求一些特殊的图形:
1.弓形:
弓形通常只求面积
弓形面积=扇形面积-三角形面积(除了半圆)
2.“弯角”:
弯角的面积=正方形-扇形
3.“谷子”:
“谷子”的面积=弓形面积×2
【典例精讲】
题型1:圆的周长面积
例1.下面正确的说法是( ).
A、等于3.14 B、周长相等的两个圆,面积也相等 C、半径是2cm的圆周长和面积相等
例2.周长相等的圆和正方形,圆的面积( )正方形面积.
A、大于 B、小于 C、等于
例3.圆的半径扩大3倍,圆的面积扩大( ).
A、3倍 B、9倍 C、27倍
例4.小圆的直径等于大圆的半径,小圆的面积与大圆面积的是( ).
A、1:2 B、1:4 C、1:8
例5.一个圆形花坛,直径5米,在它周围有一条宽1米的环形鹅卵石小路,小路的面积是多少平方米?
例6.在一块半径是5m的圆形草地的中间修一个边长为3m的正方形花坛后,草地面积还剩下多少?
例7.环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积?
例8.一根31.4米的绳子,用它围成的正方形面积大,还是围成圆的面积大?大多少?
题型2:阴影部分
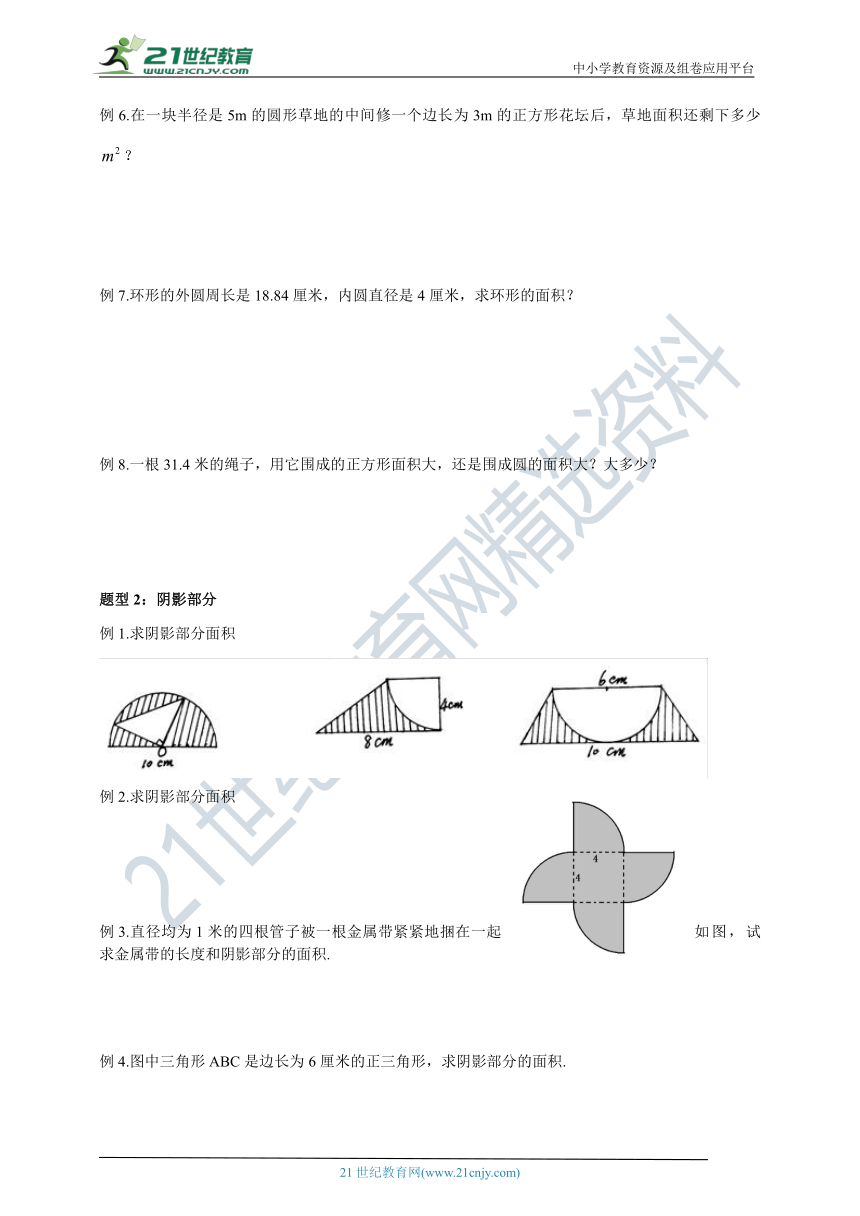
例1.求阴影部分面积
例2.求阴影部分面积
例3.直径均为1米的四根管子被一根金属带紧紧地捆在一起如图,试求金属带的长度和阴影部分的面积.
例4.图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积.
【课堂练习】
题型一:圆的周长面积
【基础练习】
1.求右图的周长,正确的列式是( )
2.圆的半径扩大3倍,圆的面积扩大( )
3.小圆的直径等于大圆的半径,小圆的面积与大圆面积的是( )
【提高练习】
1.一个圆形水池的直径是20m,沿水池走一圈,至少要走多少m?这个水池占地多少?
2.一辆自行车轮胎的外直径为72cm,如果平均每分钟转100周.通过一座2260.8m的大桥,需要几分钟?
3.一个圆形花坛,直径5米,在它周围有一条宽1米的环形鹅卵石小路,小路的面积是多少平方米?
4.在一个直径为20厘米的圆内剪一个最大的正方形,正方形的面积占圆面积的几分之几?
5.从一张长3厘米、宽2.5厘米的长方形纸片上剪下一个最大的正方形,求这个正方形的周长.
6.一个平行四边形和一个三角形等底等高。已知平行四边形面积是25 ,三角形的面积是多少?
题型二:阴影部分
【基础练习】
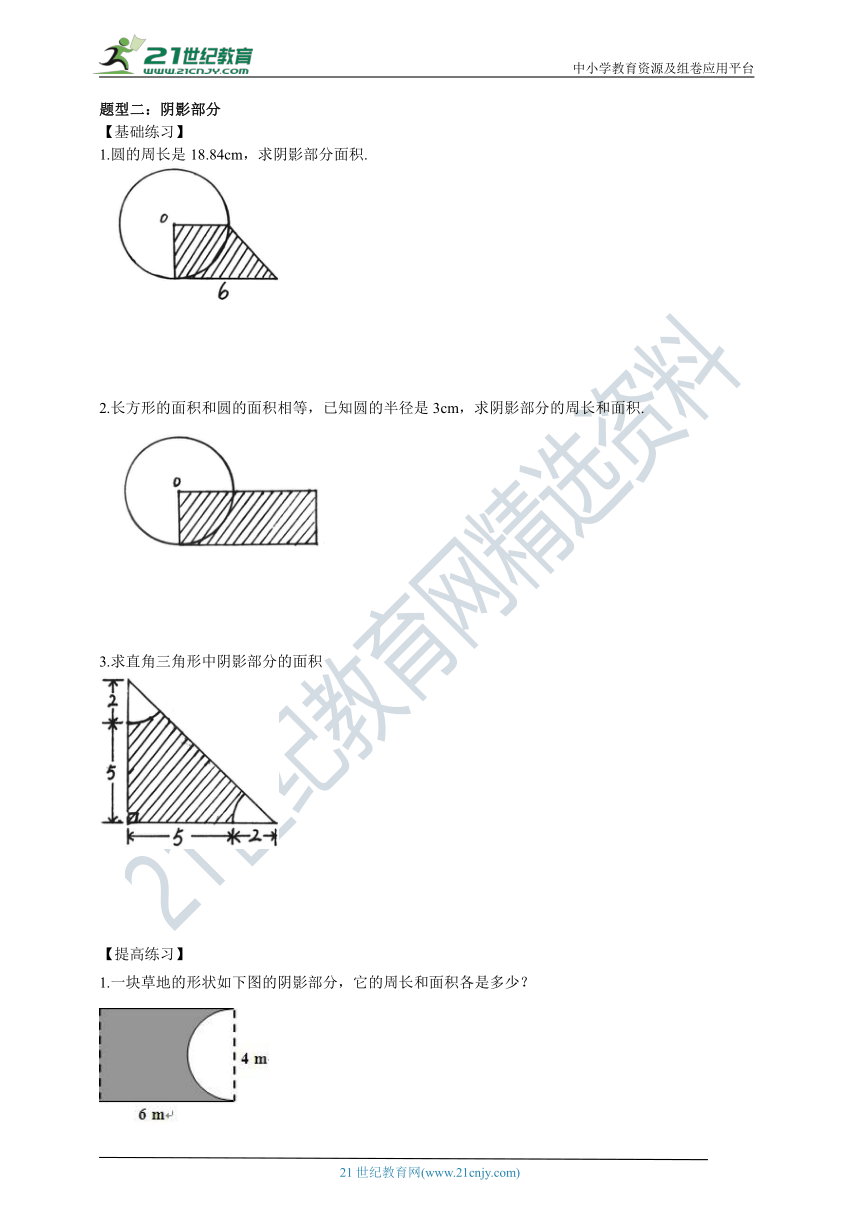
1.圆的周长是18.84cm,求阴影部分面积.
2.长方形的面积和圆的面积相等,已知圆的半径是3cm,求阴影部分的周长和面积.
3.求直角三角形中阴影部分的面积
【提高练习】
1.一块草地的形状如下图的阴影部分,它的周长和面积各是多少?
2.张师傅、李师傅、王师傅分别从同样大小的正方形钢板上冲制1个圆、4个圆、9个圆或一个最大的1/4圆(如图),谁剩下的边角料多?为什么?
3.求右图阴影部分的面积
4.如图已知圆的直径为6cm,求阴影部分的面积
5.求阴影部分的面积
6.右下图中阴影部分的面积是50cm2,求环形的面积.
参考答案
【典例精讲】
例1.【答案】:B.
【解析】:A、约等于3.14,A错误;B、周长相等的两个圆,半径相等,面积也相等;C、半径是2cm圆周长和面积的单位不一样,C错误.
例2.【答案】:A.
【解析】:周长相等的圆是正方形和圆,圆的面积大于正方形面积.
例3.【答案】:B.
【解析】:圆的半径扩大3倍,圆的面积扩大半径的平方倍,扩大9倍.
例4.【答案】:B
【解析】:小圆的直径等于大圆的半径,小圆的半径是大圆半径的一半,那么小圆的面积与大圆面积的比是1:4.
例5.【答案】:圆环的面积为:
【解析】:求小路的面积就是求圆环的面积
例6.【答案】:
【解析】:圆形中间修了一个正方形.
例7.【答案】:15.7平方厘米.
【解析】:通过外圆圆周长求出外圆半径,再求环形面积.
例8.【答案】:围成圆面积大,大16.8775平方米;
【解析】:31.4分别是圆和正方形的周长再去算各自面积.
例8.【答案】:(1)264平方厘米;(2)11.44平方厘米;(3)9.87平方厘米;
【解析】:(1)半圆面积减三角形面积;(2)梯形面积减四分之一圆面积;(3)梯形面积减半圆面积
例9.【答案】:(1)25平方厘米;(2)32平方厘米;(3)14.13平方厘米.
【解析】:(1)面积割补,组成三角形;(2)面积割补组成三角形面积;(3)环形面积一半.
例10.【答案】:(1)2.28平方厘米;(2)45.25平方厘米;(3)6.28平方厘米;
【解析】:(1)谷子模型;(2)组合图形,上面一个半圆面积加三角形面积;(3)阴影部分组成一个半圆;
例11.【答案】:66.24.
【解析】:分割成一个正方形面积加一个圆的面积.
例12.【答案】:0.215平方米.
【解析】:阴影部分分割成一个正方形减圆剩的面积.
例13.【答案】:37.68平方厘米.
【解析】:求扇形面积.
【课堂练习】
【题型1】
【基础练习】
1.【解析】:
2.【解析】:
3.【解析】:小圆和大圆半径之比为,小圆和大圆面积之比为
【提高练习】
1.【解析】:周长:米,面积:平方米.
2.【解析】:周长:厘米
每分钟路程:
通过桥所用的时间:.
3.【解析】:.
4.【解析】:正方形面积:200平方厘米;圆的面积:314平方厘米;正方形面积占圆的面积
5.【解析】:10厘米.
6.【解析】:25÷2=12.5平方厘米
【题型1】
【基础练习】
1.【解析】:
2.【解析】:周长:24.84厘米;面积:28.26平方厘米.
3.【解析】:21.36.
【提高练习】
1.【解析】:周长:22.28m;面积:17.72平方米.
2.【解析】:一样多;设边长为12a,余料面积相同.
3.【解析】:两个半圆面积加三角形面积减去大半圆面积:96.
4.【解析】:
5.【解析】:
6.【解析】:50π=157平方厘米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二讲 圆的面积
【知识巩固】
圆面积:
圆环的面积为:
扇形的面积为:
半圆面积:,90°扇形面积
求一些特殊的图形:
1.弓形:
弓形通常只求面积
弓形面积=扇形面积-三角形面积(除了半圆)
2.“弯角”:
弯角的面积=正方形-扇形
3.“谷子”:
“谷子”的面积=弓形面积×2
【典例精讲】
题型1:圆的周长面积
例1.下面正确的说法是( ).
A、等于3.14 B、周长相等的两个圆,面积也相等 C、半径是2cm的圆周长和面积相等
例2.周长相等的圆和正方形,圆的面积( )正方形面积.
A、大于 B、小于 C、等于
例3.圆的半径扩大3倍,圆的面积扩大( ).
A、3倍 B、9倍 C、27倍
例4.小圆的直径等于大圆的半径,小圆的面积与大圆面积的是( ).
A、1:2 B、1:4 C、1:8
例5.一个圆形花坛,直径5米,在它周围有一条宽1米的环形鹅卵石小路,小路的面积是多少平方米?
例6.在一块半径是5m的圆形草地的中间修一个边长为3m的正方形花坛后,草地面积还剩下多少?
例7.环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积?
例8.一根31.4米的绳子,用它围成的正方形面积大,还是围成圆的面积大?大多少?
题型2:阴影部分
例1.求阴影部分面积
例2.求阴影部分面积
例3.直径均为1米的四根管子被一根金属带紧紧地捆在一起如图,试求金属带的长度和阴影部分的面积.
例4.图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积.
【课堂练习】
题型一:圆的周长面积
【基础练习】
1.求右图的周长,正确的列式是( )
2.圆的半径扩大3倍,圆的面积扩大( )
3.小圆的直径等于大圆的半径,小圆的面积与大圆面积的是( )
【提高练习】
1.一个圆形水池的直径是20m,沿水池走一圈,至少要走多少m?这个水池占地多少?
2.一辆自行车轮胎的外直径为72cm,如果平均每分钟转100周.通过一座2260.8m的大桥,需要几分钟?
3.一个圆形花坛,直径5米,在它周围有一条宽1米的环形鹅卵石小路,小路的面积是多少平方米?
4.在一个直径为20厘米的圆内剪一个最大的正方形,正方形的面积占圆面积的几分之几?
5.从一张长3厘米、宽2.5厘米的长方形纸片上剪下一个最大的正方形,求这个正方形的周长.
6.一个平行四边形和一个三角形等底等高。已知平行四边形面积是25 ,三角形的面积是多少?
题型二:阴影部分
【基础练习】
1.圆的周长是18.84cm,求阴影部分面积.
2.长方形的面积和圆的面积相等,已知圆的半径是3cm,求阴影部分的周长和面积.
3.求直角三角形中阴影部分的面积
【提高练习】
1.一块草地的形状如下图的阴影部分,它的周长和面积各是多少?
2.张师傅、李师傅、王师傅分别从同样大小的正方形钢板上冲制1个圆、4个圆、9个圆或一个最大的1/4圆(如图),谁剩下的边角料多?为什么?
3.求右图阴影部分的面积
4.如图已知圆的直径为6cm,求阴影部分的面积
5.求阴影部分的面积
6.右下图中阴影部分的面积是50cm2,求环形的面积.
参考答案
【典例精讲】
例1.【答案】:B.
【解析】:A、约等于3.14,A错误;B、周长相等的两个圆,半径相等,面积也相等;C、半径是2cm圆周长和面积的单位不一样,C错误.
例2.【答案】:A.
【解析】:周长相等的圆是正方形和圆,圆的面积大于正方形面积.
例3.【答案】:B.
【解析】:圆的半径扩大3倍,圆的面积扩大半径的平方倍,扩大9倍.
例4.【答案】:B
【解析】:小圆的直径等于大圆的半径,小圆的半径是大圆半径的一半,那么小圆的面积与大圆面积的比是1:4.
例5.【答案】:圆环的面积为:
【解析】:求小路的面积就是求圆环的面积
例6.【答案】:
【解析】:圆形中间修了一个正方形.
例7.【答案】:15.7平方厘米.
【解析】:通过外圆圆周长求出外圆半径,再求环形面积.
例8.【答案】:围成圆面积大,大16.8775平方米;
【解析】:31.4分别是圆和正方形的周长再去算各自面积.
例8.【答案】:(1)264平方厘米;(2)11.44平方厘米;(3)9.87平方厘米;
【解析】:(1)半圆面积减三角形面积;(2)梯形面积减四分之一圆面积;(3)梯形面积减半圆面积
例9.【答案】:(1)25平方厘米;(2)32平方厘米;(3)14.13平方厘米.
【解析】:(1)面积割补,组成三角形;(2)面积割补组成三角形面积;(3)环形面积一半.
例10.【答案】:(1)2.28平方厘米;(2)45.25平方厘米;(3)6.28平方厘米;
【解析】:(1)谷子模型;(2)组合图形,上面一个半圆面积加三角形面积;(3)阴影部分组成一个半圆;
例11.【答案】:66.24.
【解析】:分割成一个正方形面积加一个圆的面积.
例12.【答案】:0.215平方米.
【解析】:阴影部分分割成一个正方形减圆剩的面积.
例13.【答案】:37.68平方厘米.
【解析】:求扇形面积.
【课堂练习】
【题型1】
【基础练习】
1.【解析】:
2.【解析】:
3.【解析】:小圆和大圆半径之比为,小圆和大圆面积之比为
【提高练习】
1.【解析】:周长:米,面积:平方米.
2.【解析】:周长:厘米
每分钟路程:
通过桥所用的时间:.
3.【解析】:.
4.【解析】:正方形面积:200平方厘米;圆的面积:314平方厘米;正方形面积占圆的面积
5.【解析】:10厘米.
6.【解析】:25÷2=12.5平方厘米
【题型1】
【基础练习】
1.【解析】:
2.【解析】:周长:24.84厘米;面积:28.26平方厘米.
3.【解析】:21.36.
【提高练习】
1.【解析】:周长:22.28m;面积:17.72平方米.
2.【解析】:一样多;设边长为12a,余料面积相同.
3.【解析】:两个半圆面积加三角形面积减去大半圆面积:96.
4.【解析】:
5.【解析】:
6.【解析】:50π=157平方厘米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
