北师大版九年级上册数学同步练习2.3 第3课时 一元二次方程的应用——几何面积设计方案(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学同步练习2.3 第3课时 一元二次方程的应用——几何面积设计方案(Word版 含答案 ) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 00:00:00 | ||
图片预览

文档简介
北师大版九年级上册数学同步练习
第3课时 一元二次方程的应用——几何面积设计方案
一、选择题
1.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1
m的正方形后,剩下的部分刚好能围成一个容积为15
m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2
m.现已知购买这种铁皮每平方米需20元钱,问张大叔购买这张矩形铁皮共花了
( )
A.500元
B.600元
C.700元
D.800元
2.在“两学一做”活动中,某社区居民在一幅长90
cm、宽40
cm的矩形形状的宣传画的四周加上宽度相同的边框,制成一幅挂图(如图).如果宣传画的面积占这个挂图面积的72%,所加边框的宽度为x
cm,则根据题意列出的方程是
( )
A.(90+x)(40+x)=90×40×72%
B.(90-2x)(40-2x)=90×40×72%
C.(90+2x)(40+2x)×72%=90×40
D.(90+x)(40+x)×72%=90×40
3.如图,某小区计划在一块长为32
m、宽为20
m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570
m2.若设道路的宽为x
m,则下面所列方程正确的是
( )
A.(32-2x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x2=570
4.如图,在长为100
m、宽为80
m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644
m2,则道路的宽应为
( )
A.178
m
B.98
m
C.2
m
D.78
m
5.小芳妈妈要给一幅长为60
cm、宽为40
cm的矩形十字绣的四周装裱一条宽度相同的金色边框制成一幅矩形挂图,使整幅挂图的面积是3400
cm2.设金色边框的宽度为x
cm,则x满足的方程是
( )
A.x2+50x-1400=0
B.x2-65x-250=0
C.x2-30x-1400=0
D.x2+50x-250=0
二、填空题
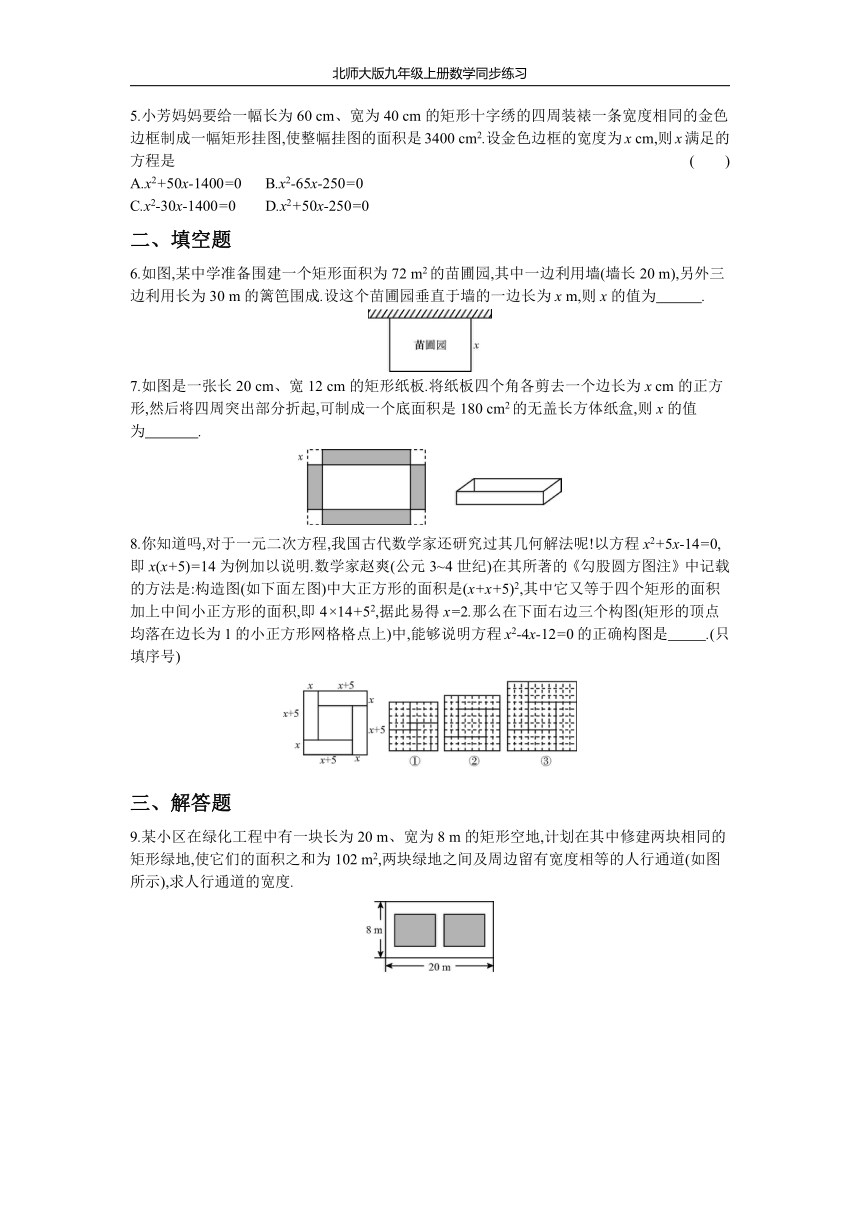
6.如图,某中学准备围建一个矩形面积为72
m2的苗圃园,其中一边利用墙(墙长20
m),另外三边利用长为30
m的篱笆围成.设这个苗圃园垂直于墙的一边长为x
m,则x的值为
.?
7.如图是一张长20
cm、宽12
cm的矩形纸板.将纸板四个角各剪去一个边长为x
cm的正方形,然后将四周突出部分折起,可制成一个底面积是180
cm2的无盖长方体纸盒,则x的值为
.?
8.你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程x2+5x-14=0,即x(x+5)=14为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2-4x-12=0的正确构图是
.(只填序号)?
三、解答题
9.某小区在绿化工程中有一块长为20
m、宽为8
m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为102
m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
10.已知一个矩形周长为56
cm.
(1)当矩形面积为180
cm2时,矩形的长和宽分别为多少?
(2)这个矩形的面积能是200
cm2吗?请说明理由.
11.如图1,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
(1)若围成花圃的面积为40平方米,求BC的长.
(2)如图2,若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃面积为50平方米,请你判断能否成功围成花圃?如果能,求BC的长;如果不能,请说明理由.
12.在一块长16
m、宽12
m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半,图1、图2分别是小明和小颖的设计方案.
(1)你认为小明的结果对吗?请说明理由.
(2)请你帮助小颖求出图中的x.(精确到0.1
m)
(3)你还有其他的设计方案吗?请在图中画出你的设计草图,并加以说明.
参考答案
一、选择题
题号
1
2
3
4
5
答案
C
C
A
C
D
二、填空题
6. 12
7. 1
8. ②
三、解答题
9.解:设人行通道的宽度为x
m,
根据题意得(20-3x)(8-2x)=102,
解得x1=1,x2=(不合题意,舍去).
答:人行通道的宽度为1
m.
10.解:(1)设矩形的长为x
cm,则宽为(28-x)cm,
依题意有x(28-x)=180,解得x1=10(舍去),x2=18,
28-x=28-18=10
cm.
故这个矩形的长为18
cm、宽为10
cm.
(2)设矩形的长为x
cm,则宽为(28-x)cm,
依题意有x(28-x)=200,即x2-28x+200=0,
则Δ=282-4×200=784-800<0,原方程无解,
故这个矩形的面积不能是200
cm2.
11.解:(1)设BC的长为x米,则AB的长为米.
根据题意,得x·=40,
解得x1=4,x2=20(舍去),∴BC的长为4米.
(2)不能围成.理由如下:
设BC的长为y米,则AB的长为米.
根据题意,得y·=50,整理得y2-24y+150=0.
∵Δ=(-24)2-4×1×150=-24<0,∴该方程无实数根,
∴不能围成面积为50平方米的花圃.
12.解:(1)小明的结果不对.设小路的宽为x
m,
则得方程(16-2x)(12-2x)=×16×12,
解得x1=2,x2=12.
∵荒地的宽为12
m,若小路宽为12
m,不符合实际情况,故x2=12
m不符合题意,应舍去,
∴小路的宽为2
m.
(2)由题意得4××16×12,x2=,
∴x≈5.5
m.(负值舍去)
(3)方案不唯一.如图,可取矩形的边AB的中点E,连接EC,ED.
第3课时 一元二次方程的应用——几何面积设计方案
一、选择题
1.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1
m的正方形后,剩下的部分刚好能围成一个容积为15
m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2
m.现已知购买这种铁皮每平方米需20元钱,问张大叔购买这张矩形铁皮共花了
( )
A.500元
B.600元
C.700元
D.800元
2.在“两学一做”活动中,某社区居民在一幅长90
cm、宽40
cm的矩形形状的宣传画的四周加上宽度相同的边框,制成一幅挂图(如图).如果宣传画的面积占这个挂图面积的72%,所加边框的宽度为x
cm,则根据题意列出的方程是
( )
A.(90+x)(40+x)=90×40×72%
B.(90-2x)(40-2x)=90×40×72%
C.(90+2x)(40+2x)×72%=90×40
D.(90+x)(40+x)×72%=90×40
3.如图,某小区计划在一块长为32
m、宽为20
m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570
m2.若设道路的宽为x
m,则下面所列方程正确的是
( )
A.(32-2x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x2=570
4.如图,在长为100
m、宽为80
m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644
m2,则道路的宽应为
( )
A.178
m
B.98
m
C.2
m
D.78
m
5.小芳妈妈要给一幅长为60
cm、宽为40
cm的矩形十字绣的四周装裱一条宽度相同的金色边框制成一幅矩形挂图,使整幅挂图的面积是3400
cm2.设金色边框的宽度为x
cm,则x满足的方程是
( )
A.x2+50x-1400=0
B.x2-65x-250=0
C.x2-30x-1400=0
D.x2+50x-250=0
二、填空题
6.如图,某中学准备围建一个矩形面积为72
m2的苗圃园,其中一边利用墙(墙长20
m),另外三边利用长为30
m的篱笆围成.设这个苗圃园垂直于墙的一边长为x
m,则x的值为
.?
7.如图是一张长20
cm、宽12
cm的矩形纸板.将纸板四个角各剪去一个边长为x
cm的正方形,然后将四周突出部分折起,可制成一个底面积是180
cm2的无盖长方体纸盒,则x的值为
.?
8.你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程x2+5x-14=0,即x(x+5)=14为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2-4x-12=0的正确构图是
.(只填序号)?
三、解答题
9.某小区在绿化工程中有一块长为20
m、宽为8
m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为102
m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
10.已知一个矩形周长为56
cm.
(1)当矩形面积为180
cm2时,矩形的长和宽分别为多少?
(2)这个矩形的面积能是200
cm2吗?请说明理由.
11.如图1,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
(1)若围成花圃的面积为40平方米,求BC的长.
(2)如图2,若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃面积为50平方米,请你判断能否成功围成花圃?如果能,求BC的长;如果不能,请说明理由.
12.在一块长16
m、宽12
m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半,图1、图2分别是小明和小颖的设计方案.
(1)你认为小明的结果对吗?请说明理由.
(2)请你帮助小颖求出图中的x.(精确到0.1
m)
(3)你还有其他的设计方案吗?请在图中画出你的设计草图,并加以说明.
参考答案
一、选择题
题号
1
2
3
4
5
答案
C
C
A
C
D
二、填空题
6. 12
7. 1
8. ②
三、解答题
9.解:设人行通道的宽度为x
m,
根据题意得(20-3x)(8-2x)=102,
解得x1=1,x2=(不合题意,舍去).
答:人行通道的宽度为1
m.
10.解:(1)设矩形的长为x
cm,则宽为(28-x)cm,
依题意有x(28-x)=180,解得x1=10(舍去),x2=18,
28-x=28-18=10
cm.
故这个矩形的长为18
cm、宽为10
cm.
(2)设矩形的长为x
cm,则宽为(28-x)cm,
依题意有x(28-x)=200,即x2-28x+200=0,
则Δ=282-4×200=784-800<0,原方程无解,
故这个矩形的面积不能是200
cm2.
11.解:(1)设BC的长为x米,则AB的长为米.
根据题意,得x·=40,
解得x1=4,x2=20(舍去),∴BC的长为4米.
(2)不能围成.理由如下:
设BC的长为y米,则AB的长为米.
根据题意,得y·=50,整理得y2-24y+150=0.
∵Δ=(-24)2-4×1×150=-24<0,∴该方程无实数根,
∴不能围成面积为50平方米的花圃.
12.解:(1)小明的结果不对.设小路的宽为x
m,
则得方程(16-2x)(12-2x)=×16×12,
解得x1=2,x2=12.
∵荒地的宽为12
m,若小路宽为12
m,不符合实际情况,故x2=12
m不符合题意,应舍去,
∴小路的宽为2
m.
(2)由题意得4××16×12,x2=,
∴x≈5.5
m.(负值舍去)
(3)方案不唯一.如图,可取矩形的边AB的中点E,连接EC,ED.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
