北师大版九年级上册数学同步练习2.6 第1课时 数字问题与几何图形的面积问题(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学同步练习2.6 第1课时 数字问题与几何图形的面积问题(Word版 含答案 ) |  | |
| 格式 | zip | ||
| 文件大小 | 125.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 12:59:07 | ||
图片预览

文档简介
北师大版九年级上册数学同步练习
2.6 应用一元二次方程
第1课时 数字问题与几何图形的面积问题
一、选择题
1.如图,在一幅长为80厘米、宽为50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是
( )
A.x2+130x-1400=0
B.x2+65x-350=0
C.x2-130x-1400=0
D.x2-65x-350=0
2.毕业典礼后,九年级(1)班有若干人,若每人给全班的其他成员赠送一张毕业纪念卡,则全班共送贺卡1190张.问九年级(1)班的人数为
( )
A.34
B.35
C.36
D.37
3.如图,在△ABC中,∠ABC=90°,AB=8
cm,BC=6
cm.动点P,Q分别从点A,B同时开始运动,点P的速度为1
cm/s,点Q的速度为2
cm/s,点Q移动到点C后停止,点P也随之停止运动.下列时间中,能使△PBQ的面积为15
cm2的是
( )
A.2
s
B.3
s
C.4
s
D.5
s
4.已知小龙、阿虎两人均在同一地点,若小龙向北直走160
m,再向东直走80
m后可到百货商场,则阿虎向西直走多远后,他与百货商场的距离为340
m?
( )
A.100
m
B.180
m
C.220
m
D.260
m
5.若一个直角三角形的两条直角边长之和为14,面积为24,则其斜边的长是
( )
A.2
B.4
C.8
D.10
6.“泱泱华夏,浩浩千秋.于以求之?旸谷之东.山其何辉,韫卞和之美玉……”这是武汉16岁女孩陈天羽用文言文写70周年阅兵的观后感.小汀州同学把这篇气势磅礴、文采飞扬的文章放到自己的微博上,并决定用微博转发的方式传播.他设计了如下的传播规则:将文章发表在自己的微博上,再邀请n个好友转发,每个好友转发之后,又邀请n个互不相同的好友转发,依此类推.已知经过两轮转发后,共有111个人参与了宣传活动,则n的值为
( )
A.9
B.10
C.11
D.12
二、填空题
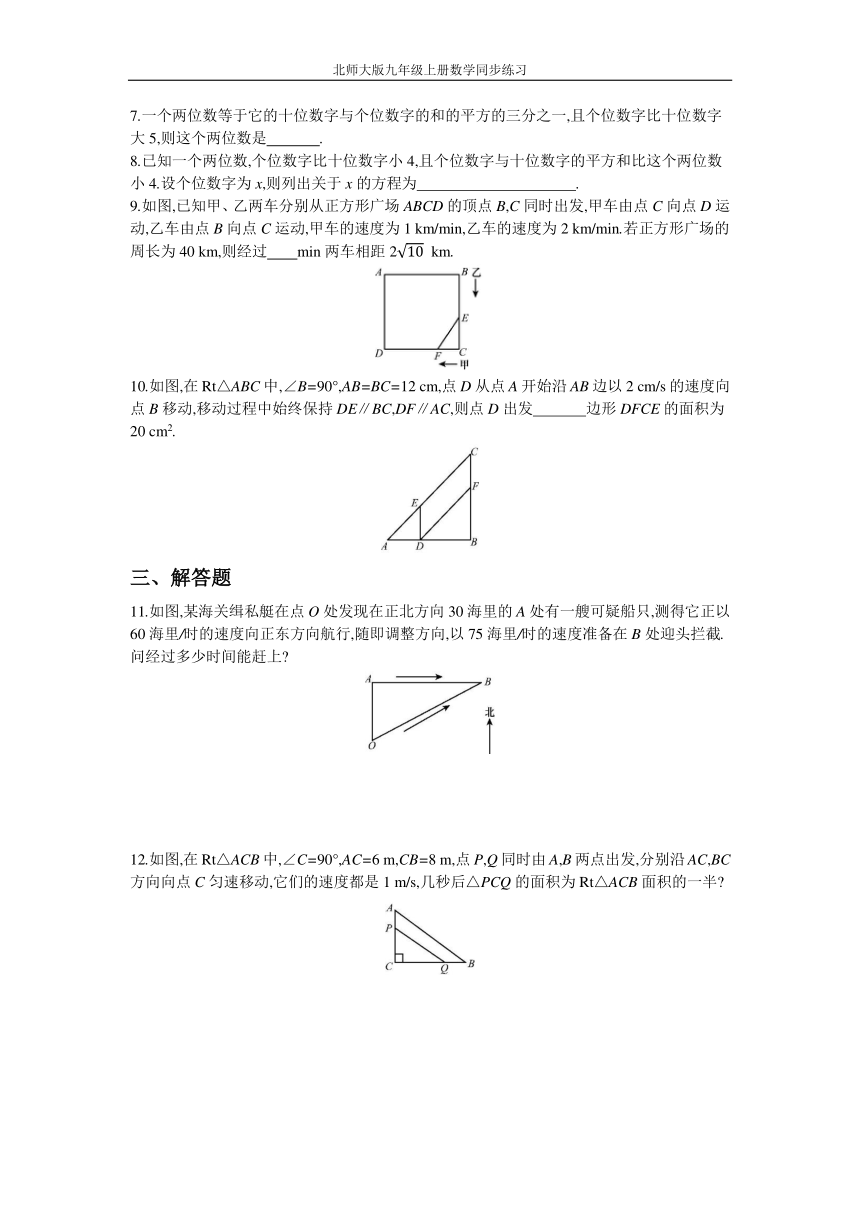
7.一个两位数等于它的十位数字与个位数字的和的平方的三分之一,且个位数字比十位数字大5,则这个两位数是
.?
8.已知一个两位数,个位数字比十位数字小4,且个位数字与十位数字的平方和比这个两位数小4.设个位数字为x,则列出关于x的方程为
.
9.如图,已知甲、乙两车分别从正方形广场ABCD的顶点B,C同时出发,甲车由点C向点D运动,乙车由点B向点C运动,甲车的速度为1
km/min,乙车的速度为2
km/min.若正方形广场的周长为40
km,则经过 min两车相距2
km.?
10.如图,在Rt△ABC中,∠B=90°,AB=BC=12
cm,点D从点A开始沿AB边以2
cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,则点D出发
边形DFCE的面积为20
cm2.?
三、解答题
11.如图,某海关缉私艇在点O处发现在正北方向30海里的A处有一艘可疑船只,测得它正以60海里/时的速度向正东方向航行,随即调整方向,以75海里/时的速度准备在B处迎头拦截.问经过多少时间能赶上?
12.如图,在Rt△ACB中,∠C=90°,AC=6
m,CB=8
m,点P,Q同时由A,B两点出发,分别沿AC,BC方向向点C匀速移动,它们的速度都是1
m/s,几秒后△PCQ的面积为Rt△ACB面积的一半?
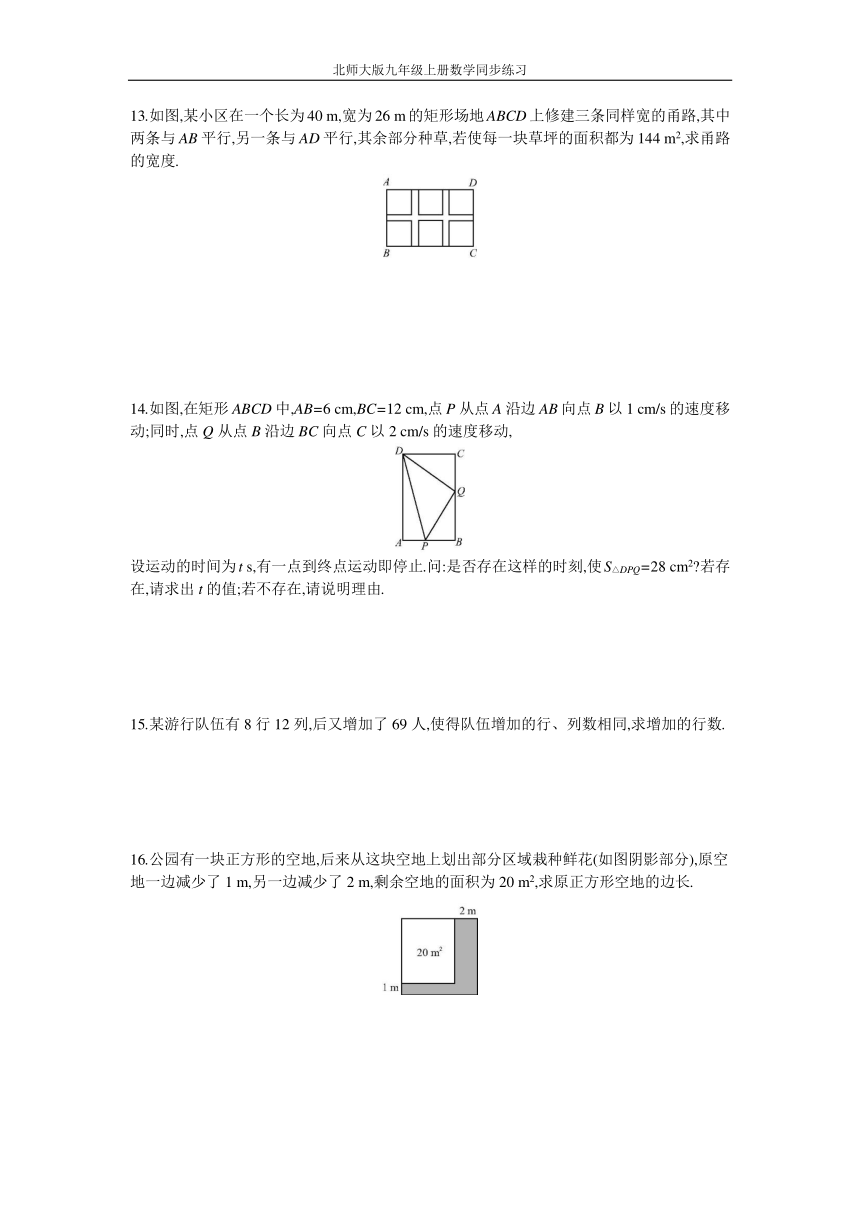
13.如图,某小区在一个长为40
m,宽为26
m的矩形场地ABCD上修建三条同样宽的甬路,其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144
m2,求甬路的宽度.
14.如图,在矩形ABCD中,AB=6
cm,BC=12
cm,点P从点A沿边AB向点B以1
cm/s的速度移动;同时,点Q从点B沿边BC向点C以2
cm/s的速度移动,
设运动的时间为t
s,有一点到终点运动即停止.问:是否存在这样的时刻,使S△DPQ=28
cm2?若存在,请求出t的值;若不存在,请说明理由.
15.某游行队伍有8行12列,后又增加了69人,使得队伍增加的行、列数相同,求增加的行数.
16.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了1
m,另一边减少了2
m,剩余空地的面积为20
m2,求原正方形空地的边长.
17.小林准备进行如下实验操作:把一根长为40
cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58
cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48
cm2.”他的说法正确吗?请说明理由.
18.如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25
m,另外三面用长度为50
m的篱笆围成.(篱笆正好要全部用完,且不考虑接头的部分)
(1)若矩形羊圈的面积为300
m2,则垂直于墙的一边AB的长为多少?
(2)农场老板又想将羊圈ABCD的面积扩大到320
m2,从而可以养更多的羊.请聪明的你告诉他,他的这个想法能实现吗?为什么?
参考答案
一、选择题
题号
1
2
3
4
5
6
答案
B
B
B
C
D
B
二、填空题
7. 27
8. x2+(x+4)2=x+10(x+4)-4
9. 2
10. 1或5
三、解答题
11.设经过x小时能赶上,则OB=75x,AB=60x,
在直角△ABO中,OB2=OA2+AB2,则(75x)2=302+(60x)2,
解得x1=,x2=-(不合题意,舍去).
答:经过小时缉私队赶上可疑船只.
12.设x
s后△PCQ的面积为Rt△ACB面积的一半,
依题意,得(8-x)(6-x)=×8×6,
整理,得x2-14x+24=0,即(x-12)(x-2)=0,
解得x1=12,x2=2.
但x=12不符合题意,舍去,所以x=2.
答:2
s后△PCQ的面积为Rt△ACB面积的一半.
13.设甬路的宽为x
m,
依题意,得40×26-(40x+2×26x-2x2)=144×6,
整理,得x2-46x+88=0,解得x1=44,x2=2.
因为甬路的宽必须小于
m,即小于20
m,
所以x=44不符合题意,舍去,所以x=2.
答:甬路的宽为2
m.
14.解:存在.
理由:设x
s时△DPQ的面积为28
cm2,
即S矩形ABCD-S△ADP-S△PBQ-S△DCQ=12×6-×12x-(6-x)·2x-×6×(12-2x)=28,整理,得x2-6x+8=0,
解得x1=2,x2=4.
当其运动2
s或4
s时均符合题意,
所以2
s或4
s时,△DPQ的面积为28
cm2.
15.解:设队伍增加的行数为x,则增加的列数也为x,
根据题意,得(8+x)(12+x)=8×12+69,
解得x1=-23(舍去),x2=3.
答:增加了3行.
16.解:设原正方形空地的边长为x
m.
根据题意,得
(x-1)(x-2)=20,
解方程,得
x1=6,x2=-3(不符合题意,舍去).
答:原正方形空地的边长为6
m.
17.解:(1)设其中一个正方形的边长为x
cm,则另一个正方形的边长为(10-x)cm.
由题意得x2+(10-x)2=58,解得x1=3,x2=7,
则4×3=12,4×7=28,
所以小林应把绳子剪成12
cm和28
cm的两段.
(2)小峰的说法正确.理由:略.
18.解:(1)设所围矩形ABCD的边AB为x
m,则边AD为(50-2x)m.
依题意,得x·(50-2x)=300,即x2-25x+150=0,
解得x1=15,x2=10.
∵墙的长度不超过25
m,
∴x2=10不合题意,应舍去,
∴垂直于墙的一边AB的长为15
m.
(2)不能.
理由:略.
2.6 应用一元二次方程
第1课时 数字问题与几何图形的面积问题
一、选择题
1.如图,在一幅长为80厘米、宽为50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是
( )
A.x2+130x-1400=0
B.x2+65x-350=0
C.x2-130x-1400=0
D.x2-65x-350=0
2.毕业典礼后,九年级(1)班有若干人,若每人给全班的其他成员赠送一张毕业纪念卡,则全班共送贺卡1190张.问九年级(1)班的人数为
( )
A.34
B.35
C.36
D.37
3.如图,在△ABC中,∠ABC=90°,AB=8
cm,BC=6
cm.动点P,Q分别从点A,B同时开始运动,点P的速度为1
cm/s,点Q的速度为2
cm/s,点Q移动到点C后停止,点P也随之停止运动.下列时间中,能使△PBQ的面积为15
cm2的是
( )
A.2
s
B.3
s
C.4
s
D.5
s
4.已知小龙、阿虎两人均在同一地点,若小龙向北直走160
m,再向东直走80
m后可到百货商场,则阿虎向西直走多远后,他与百货商场的距离为340
m?
( )
A.100
m
B.180
m
C.220
m
D.260
m
5.若一个直角三角形的两条直角边长之和为14,面积为24,则其斜边的长是
( )
A.2
B.4
C.8
D.10
6.“泱泱华夏,浩浩千秋.于以求之?旸谷之东.山其何辉,韫卞和之美玉……”这是武汉16岁女孩陈天羽用文言文写70周年阅兵的观后感.小汀州同学把这篇气势磅礴、文采飞扬的文章放到自己的微博上,并决定用微博转发的方式传播.他设计了如下的传播规则:将文章发表在自己的微博上,再邀请n个好友转发,每个好友转发之后,又邀请n个互不相同的好友转发,依此类推.已知经过两轮转发后,共有111个人参与了宣传活动,则n的值为
( )
A.9
B.10
C.11
D.12
二、填空题
7.一个两位数等于它的十位数字与个位数字的和的平方的三分之一,且个位数字比十位数字大5,则这个两位数是
.?
8.已知一个两位数,个位数字比十位数字小4,且个位数字与十位数字的平方和比这个两位数小4.设个位数字为x,则列出关于x的方程为
.
9.如图,已知甲、乙两车分别从正方形广场ABCD的顶点B,C同时出发,甲车由点C向点D运动,乙车由点B向点C运动,甲车的速度为1
km/min,乙车的速度为2
km/min.若正方形广场的周长为40
km,则经过 min两车相距2
km.?
10.如图,在Rt△ABC中,∠B=90°,AB=BC=12
cm,点D从点A开始沿AB边以2
cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,则点D出发
边形DFCE的面积为20
cm2.?
三、解答题
11.如图,某海关缉私艇在点O处发现在正北方向30海里的A处有一艘可疑船只,测得它正以60海里/时的速度向正东方向航行,随即调整方向,以75海里/时的速度准备在B处迎头拦截.问经过多少时间能赶上?
12.如图,在Rt△ACB中,∠C=90°,AC=6
m,CB=8
m,点P,Q同时由A,B两点出发,分别沿AC,BC方向向点C匀速移动,它们的速度都是1
m/s,几秒后△PCQ的面积为Rt△ACB面积的一半?
13.如图,某小区在一个长为40
m,宽为26
m的矩形场地ABCD上修建三条同样宽的甬路,其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144
m2,求甬路的宽度.
14.如图,在矩形ABCD中,AB=6
cm,BC=12
cm,点P从点A沿边AB向点B以1
cm/s的速度移动;同时,点Q从点B沿边BC向点C以2
cm/s的速度移动,
设运动的时间为t
s,有一点到终点运动即停止.问:是否存在这样的时刻,使S△DPQ=28
cm2?若存在,请求出t的值;若不存在,请说明理由.
15.某游行队伍有8行12列,后又增加了69人,使得队伍增加的行、列数相同,求增加的行数.
16.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了1
m,另一边减少了2
m,剩余空地的面积为20
m2,求原正方形空地的边长.
17.小林准备进行如下实验操作:把一根长为40
cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58
cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48
cm2.”他的说法正确吗?请说明理由.
18.如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25
m,另外三面用长度为50
m的篱笆围成.(篱笆正好要全部用完,且不考虑接头的部分)
(1)若矩形羊圈的面积为300
m2,则垂直于墙的一边AB的长为多少?
(2)农场老板又想将羊圈ABCD的面积扩大到320
m2,从而可以养更多的羊.请聪明的你告诉他,他的这个想法能实现吗?为什么?
参考答案
一、选择题
题号
1
2
3
4
5
6
答案
B
B
B
C
D
B
二、填空题
7. 27
8. x2+(x+4)2=x+10(x+4)-4
9. 2
10. 1或5
三、解答题
11.设经过x小时能赶上,则OB=75x,AB=60x,
在直角△ABO中,OB2=OA2+AB2,则(75x)2=302+(60x)2,
解得x1=,x2=-(不合题意,舍去).
答:经过小时缉私队赶上可疑船只.
12.设x
s后△PCQ的面积为Rt△ACB面积的一半,
依题意,得(8-x)(6-x)=×8×6,
整理,得x2-14x+24=0,即(x-12)(x-2)=0,
解得x1=12,x2=2.
但x=12不符合题意,舍去,所以x=2.
答:2
s后△PCQ的面积为Rt△ACB面积的一半.
13.设甬路的宽为x
m,
依题意,得40×26-(40x+2×26x-2x2)=144×6,
整理,得x2-46x+88=0,解得x1=44,x2=2.
因为甬路的宽必须小于
m,即小于20
m,
所以x=44不符合题意,舍去,所以x=2.
答:甬路的宽为2
m.
14.解:存在.
理由:设x
s时△DPQ的面积为28
cm2,
即S矩形ABCD-S△ADP-S△PBQ-S△DCQ=12×6-×12x-(6-x)·2x-×6×(12-2x)=28,整理,得x2-6x+8=0,
解得x1=2,x2=4.
当其运动2
s或4
s时均符合题意,
所以2
s或4
s时,△DPQ的面积为28
cm2.
15.解:设队伍增加的行数为x,则增加的列数也为x,
根据题意,得(8+x)(12+x)=8×12+69,
解得x1=-23(舍去),x2=3.
答:增加了3行.
16.解:设原正方形空地的边长为x
m.
根据题意,得
(x-1)(x-2)=20,
解方程,得
x1=6,x2=-3(不符合题意,舍去).
答:原正方形空地的边长为6
m.
17.解:(1)设其中一个正方形的边长为x
cm,则另一个正方形的边长为(10-x)cm.
由题意得x2+(10-x)2=58,解得x1=3,x2=7,
则4×3=12,4×7=28,
所以小林应把绳子剪成12
cm和28
cm的两段.
(2)小峰的说法正确.理由:略.
18.解:(1)设所围矩形ABCD的边AB为x
m,则边AD为(50-2x)m.
依题意,得x·(50-2x)=300,即x2-25x+150=0,
解得x1=15,x2=10.
∵墙的长度不超过25
m,
∴x2=10不合题意,应舍去,
∴垂直于墙的一边AB的长为15
m.
(2)不能.
理由:略.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
