北师大版九年级上册数学同步练习4.4 第1课时 三角形相似的条件1(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学同步练习4.4 第1课时 三角形相似的条件1(Word版 含答案 ) |

|
|
| 格式 | zip | ||
| 文件大小 | 175.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 13:06:40 | ||
图片预览

文档简介
北师大版九年级上册数学同步练习
4.4 探索三角形相似的条件
第1课时 三角形相似的条件1
一、选择题
1.下列各组图形中可能不相似的是
( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
2.如图,在矩形ABCD中,E,F分别是CD,BC上的点.若∠AEF=90°,则一定有
( )
A.△ADE∽△ECF
B.△ECF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△ABF
3.如图,已知D是△ABC中边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于点E,交AD于点F,那么下列结论中错误的是
( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
4.如图,在?ABCD中,E是BC延长线上一点,连接AE交CD于点F,则图中相似的三角形共有
( )
A.1对
B.2对
C.3对
D.4对
5.如图,E为矩形ABCD边CD的延长线上一点,BE交AD于点G,AF⊥BE于点F,则图中与△EDG相似的三角形共有
( )
A.2个
B.3个
C.4个
D.5个
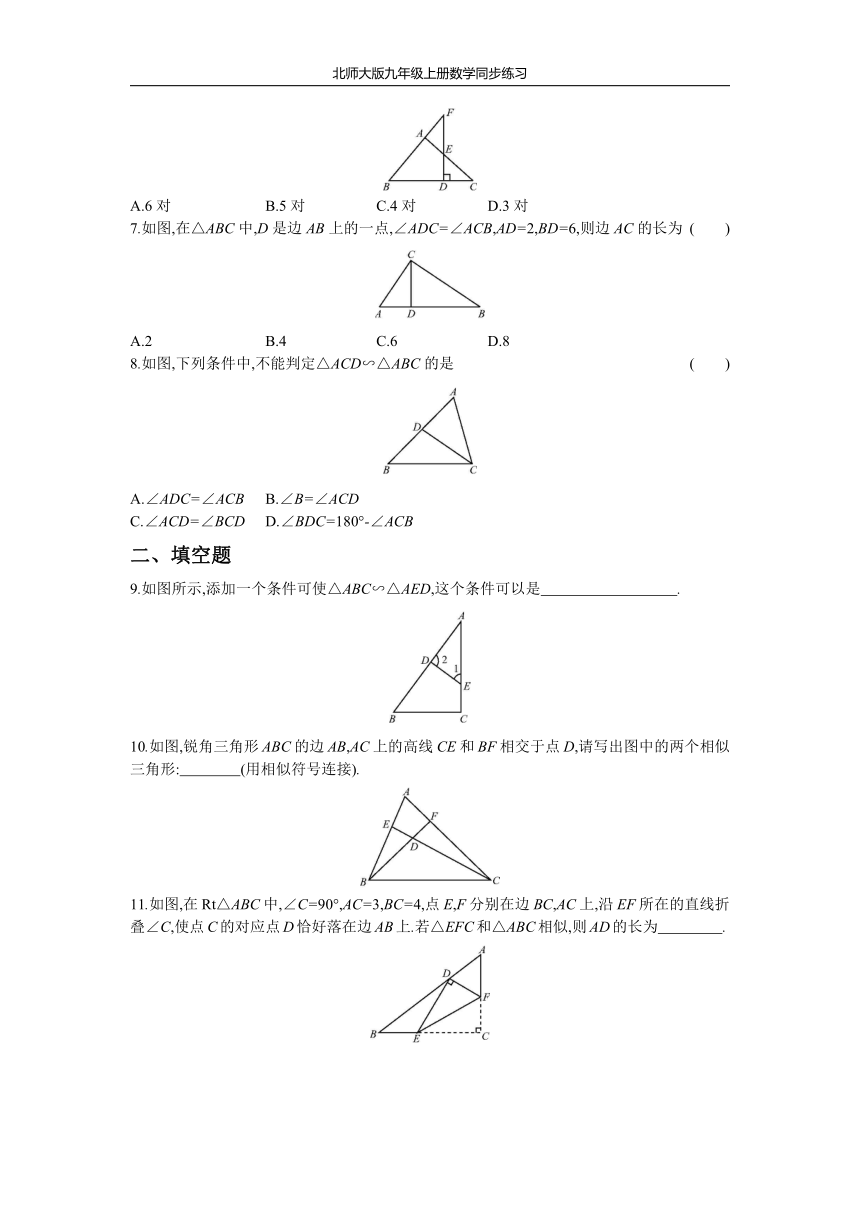
6.如图,在△ABC中,∠BAC=90°,F是BA的延长线上一点,FD⊥BC于点D,交AC于点E,则图中相似的三角形共有
( )
A.6对
B.5对
C.4对
D.3对
7.如图,在△ABC中,D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为
( )
A.2
B.4
C.6
D.8
8.如图,下列条件中,不能判定△ACD∽△ABC的是
( )
A.∠ADC=∠ACB
B.∠B=∠ACD
C.∠ACD=∠BCD
D.∠BDC=180°-∠ACB
二、填空题
9.如图所示,添加一个条件可使△ABC∽△AED,这个条件可以是
.?
10.如图,锐角三角形ABC的边AB,AC上的高线CE和BF相交于点D,请写出图中的两个相似三角形: (用相似符号连接).?
11.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上.若△EFC和△ABC相似,则AD的长为?
.?
三、解答题
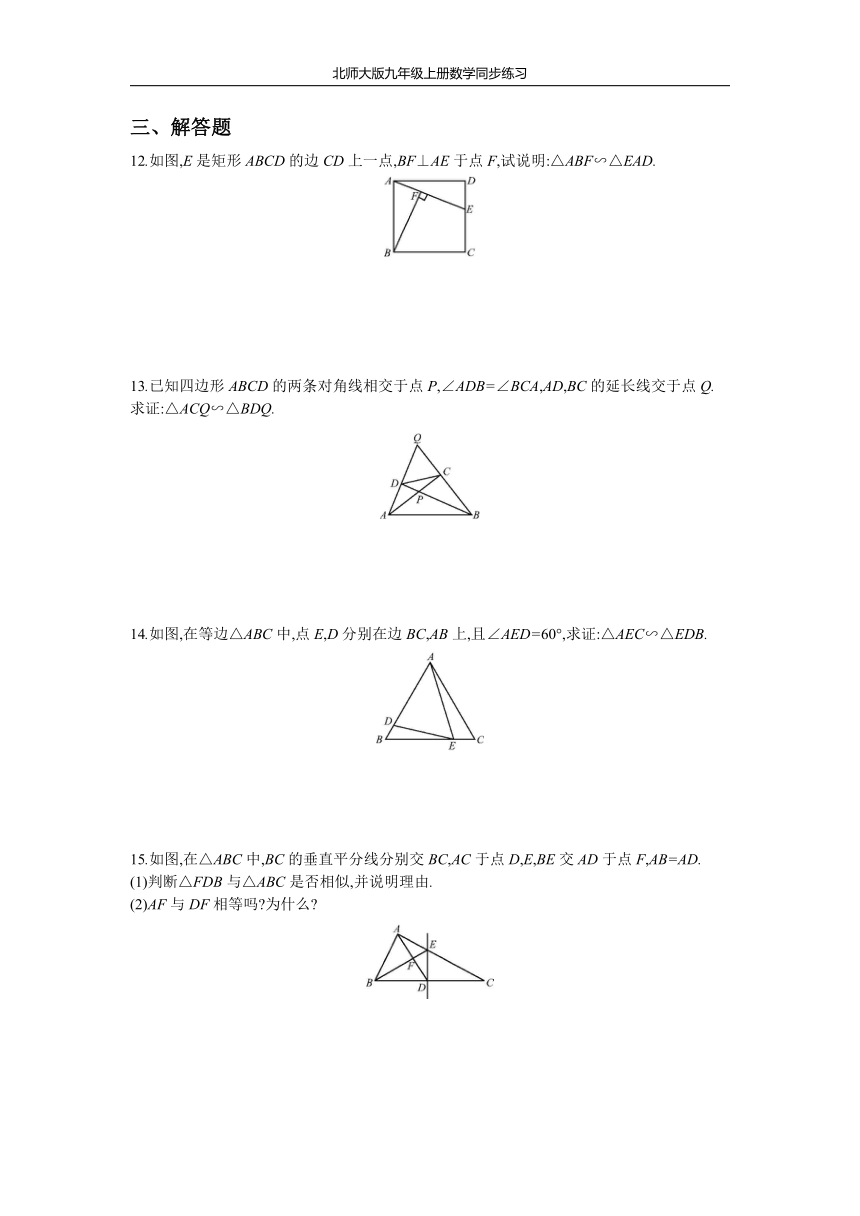
12.如图,E是矩形ABCD的边CD上一点,BF⊥AE于点F,试说明:△ABF∽△EAD.
13.已知四边形ABCD的两条对角线相交于点P,∠ADB=∠BCA,AD,BC的延长线交于点Q.
求证:△ACQ∽△BDQ.
14.如图,在等边△ABC中,点E,D分别在边BC,AB上,且∠AED=60°,求证:△AEC∽△EDB.
15.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
16.如图,平行四边形ABCD的对角线相交于点O,点E在BC边的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE.
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
A
A
C
C
A
B
C
二、填空题
9. ∠1=∠B(答案不唯一)
10.【解析】(1)在△BDE和△CDF中,∠BDE=∠CDF,∠BED=∠CFD=90°,∴△BDE∽△CDF.(2)在△ABF和△ACE中,∵∠A=∠A,∠AFB=∠AEC=90°,∴△ABF∽△ACE.类似的还有△CDF∽△CAE,△BDE∽△BAF.
【答案】△BED∽△CFD(答案不唯一)
11.?
【提示】若△EFC与△ABC相似,分两种情况:①若△CEF∽△CBA,则EF∥AB.连接CD,由折叠得CD⊥EF,∴CD⊥AB.由勾股定理得AB=5,∴CD=.在Rt△ADC中,AD=.②若△CEF∽△CAB,则∠CEF=∠A.由折叠得CD⊥EF,∴∠CEF+∠DCE=90°,又∠DCE+∠DCA=90°,∴∠CEF=∠DCA=∠A,∴AD=CD,∴在Rt△ABC中,D为AB的中点,∴AD=AB=.
三、解答题
12.∵矩形ABCD中,AB∥CD,∠D=90°,
∴∠BAF=∠AED.
∵BF⊥AE,∴∠AFB=90°,
∴∠AFB=∠D,
∴△ABF∽△EAD.
13.证明:∵∠ADB=∠BCA,∠DPA=∠CPB,
∴∠QAC=∠DBQ.
又∵∠Q=∠Q,∴△ACQ∽△BDQ.
14.证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,∴∠CAE+∠AEC=120°.
∵∠AED=60°,∴∠BED+∠AEC=180°-60°=120°,
∴∠BED=∠CAE,∴△AEC∽△EDB.
15.解:(1)△FDB∽△ABC.
理由:∵DE是BC的垂直平分线,
∴BE=CE,∴∠FBD=∠ACB.
∵AB=AD,∴∠ABC=∠FDB,∴△FDB∽△ABC.
(2)AF=DF.
理由:∵△FDB∽△ABC,
∴,∴AB=2FD.
∵AB=AD,∴AD=2FD,∴AF=DF.
16.证明:(1)∵OB=OE,∴∠OEB=∠OBE.
∵四边形ABCD是平行四边形,∴OB=OD,
∴OD=OE,∴∠OED=∠ODE.
在△BED中,∠OEB+∠OBE+∠OED+∠ODE=180°,
∴∠OEB+∠OED=90°,
即∠BED=90°,∴DE⊥BE.
(2)设OE交CD于点H,
∵OE⊥CD,∴∠CHE=90°,
∴∠CEH+∠HCE=90°.
∵∠CED=90°,∴∠CDE+∠DCE=90°,
∴∠CDE=∠CEH.
∵∠OEB=∠OBE,∴∠OBE=∠CDE.
在△CED与△DEB中,
∴△CED∽△DEB,∴,即BD·CE=CD·DE.
4.4 探索三角形相似的条件
第1课时 三角形相似的条件1
一、选择题
1.下列各组图形中可能不相似的是
( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
2.如图,在矩形ABCD中,E,F分别是CD,BC上的点.若∠AEF=90°,则一定有
( )
A.△ADE∽△ECF
B.△ECF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△ABF
3.如图,已知D是△ABC中边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于点E,交AD于点F,那么下列结论中错误的是
( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
4.如图,在?ABCD中,E是BC延长线上一点,连接AE交CD于点F,则图中相似的三角形共有
( )
A.1对
B.2对
C.3对
D.4对
5.如图,E为矩形ABCD边CD的延长线上一点,BE交AD于点G,AF⊥BE于点F,则图中与△EDG相似的三角形共有
( )
A.2个
B.3个
C.4个
D.5个
6.如图,在△ABC中,∠BAC=90°,F是BA的延长线上一点,FD⊥BC于点D,交AC于点E,则图中相似的三角形共有
( )
A.6对
B.5对
C.4对
D.3对
7.如图,在△ABC中,D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为
( )
A.2
B.4
C.6
D.8
8.如图,下列条件中,不能判定△ACD∽△ABC的是
( )
A.∠ADC=∠ACB
B.∠B=∠ACD
C.∠ACD=∠BCD
D.∠BDC=180°-∠ACB
二、填空题
9.如图所示,添加一个条件可使△ABC∽△AED,这个条件可以是
.?
10.如图,锐角三角形ABC的边AB,AC上的高线CE和BF相交于点D,请写出图中的两个相似三角形: (用相似符号连接).?
11.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上.若△EFC和△ABC相似,则AD的长为?
.?
三、解答题
12.如图,E是矩形ABCD的边CD上一点,BF⊥AE于点F,试说明:△ABF∽△EAD.
13.已知四边形ABCD的两条对角线相交于点P,∠ADB=∠BCA,AD,BC的延长线交于点Q.
求证:△ACQ∽△BDQ.
14.如图,在等边△ABC中,点E,D分别在边BC,AB上,且∠AED=60°,求证:△AEC∽△EDB.
15.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
16.如图,平行四边形ABCD的对角线相交于点O,点E在BC边的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE.
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
A
A
C
C
A
B
C
二、填空题
9. ∠1=∠B(答案不唯一)
10.【解析】(1)在△BDE和△CDF中,∠BDE=∠CDF,∠BED=∠CFD=90°,∴△BDE∽△CDF.(2)在△ABF和△ACE中,∵∠A=∠A,∠AFB=∠AEC=90°,∴△ABF∽△ACE.类似的还有△CDF∽△CAE,△BDE∽△BAF.
【答案】△BED∽△CFD(答案不唯一)
11.?
【提示】若△EFC与△ABC相似,分两种情况:①若△CEF∽△CBA,则EF∥AB.连接CD,由折叠得CD⊥EF,∴CD⊥AB.由勾股定理得AB=5,∴CD=.在Rt△ADC中,AD=.②若△CEF∽△CAB,则∠CEF=∠A.由折叠得CD⊥EF,∴∠CEF+∠DCE=90°,又∠DCE+∠DCA=90°,∴∠CEF=∠DCA=∠A,∴AD=CD,∴在Rt△ABC中,D为AB的中点,∴AD=AB=.
三、解答题
12.∵矩形ABCD中,AB∥CD,∠D=90°,
∴∠BAF=∠AED.
∵BF⊥AE,∴∠AFB=90°,
∴∠AFB=∠D,
∴△ABF∽△EAD.
13.证明:∵∠ADB=∠BCA,∠DPA=∠CPB,
∴∠QAC=∠DBQ.
又∵∠Q=∠Q,∴△ACQ∽△BDQ.
14.证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,∴∠CAE+∠AEC=120°.
∵∠AED=60°,∴∠BED+∠AEC=180°-60°=120°,
∴∠BED=∠CAE,∴△AEC∽△EDB.
15.解:(1)△FDB∽△ABC.
理由:∵DE是BC的垂直平分线,
∴BE=CE,∴∠FBD=∠ACB.
∵AB=AD,∴∠ABC=∠FDB,∴△FDB∽△ABC.
(2)AF=DF.
理由:∵△FDB∽△ABC,
∴,∴AB=2FD.
∵AB=AD,∴AD=2FD,∴AF=DF.
16.证明:(1)∵OB=OE,∴∠OEB=∠OBE.
∵四边形ABCD是平行四边形,∴OB=OD,
∴OD=OE,∴∠OED=∠ODE.
在△BED中,∠OEB+∠OBE+∠OED+∠ODE=180°,
∴∠OEB+∠OED=90°,
即∠BED=90°,∴DE⊥BE.
(2)设OE交CD于点H,
∵OE⊥CD,∴∠CHE=90°,
∴∠CEH+∠HCE=90°.
∵∠CED=90°,∴∠CDE+∠DCE=90°,
∴∠CDE=∠CEH.
∵∠OEB=∠OBE,∴∠OBE=∠CDE.
在△CED与△DEB中,
∴△CED∽△DEB,∴,即BD·CE=CD·DE.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
