北师大版九年级上册数学同步练习4.4 第4课时 黄金分割(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学同步练习4.4 第4课时 黄金分割(Word版 含答案 ) |  | |
| 格式 | zip | ||
| 文件大小 | 145.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 13:09:07 | ||
图片预览


文档简介
北师大版九年级上册数学同步练习
第4课时 黄金分割
一、选择题
1.已知点C是线段AB的黄金分割点,且AC>BC,则下列等式中成立的是
( )
A.AC2=BC·AB
B.AC2=2AB·BC
C.AB2=AC·BC
D.BC2=AC·AB
2.如图,已知线段AB=60,AD=13,DE=17,EF=7,请问在D,E,F三点中,哪一点最接近线段AB的黄金分割点
( )
A.D点
B.E点
C.F点
D.D点或F点
3.已知点P是线段AB的黄金分割点,AP>BP.记以AP为一边的正方形的面积为S1,以BP,AB的长为邻边的矩形的面积为S2,则
( )
A.S1>S2
B.S1=S2
C.S1D.S1,S2大小不能确定
4.如图所示,扇子的圆心角为α,余下扇形的圆心角为β,α与β的比通常按黄金比来设计,这样的扇子比较美观.若取黄金比为0.6,则α为
( )
A.216°
B.135°
C.120°
D.108°
5.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是≈0.618,称为黄金比例.如图,著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉与咽喉至肚脐的长度之比也是.若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为26
cm,则其身高可能是
( )
A.165
cm
B.178
cm
C.185
cm
D.190
cm
6.人以肚脐为界,下身与身高比例符合“黄金分割”比例,在人的视觉里看,是最完美的比例,身高为170
cm的人,满足“黄金分割”比例的腿长约为
( )
A.100
cm
B.104
cm
C.105
cm
D.112
cm
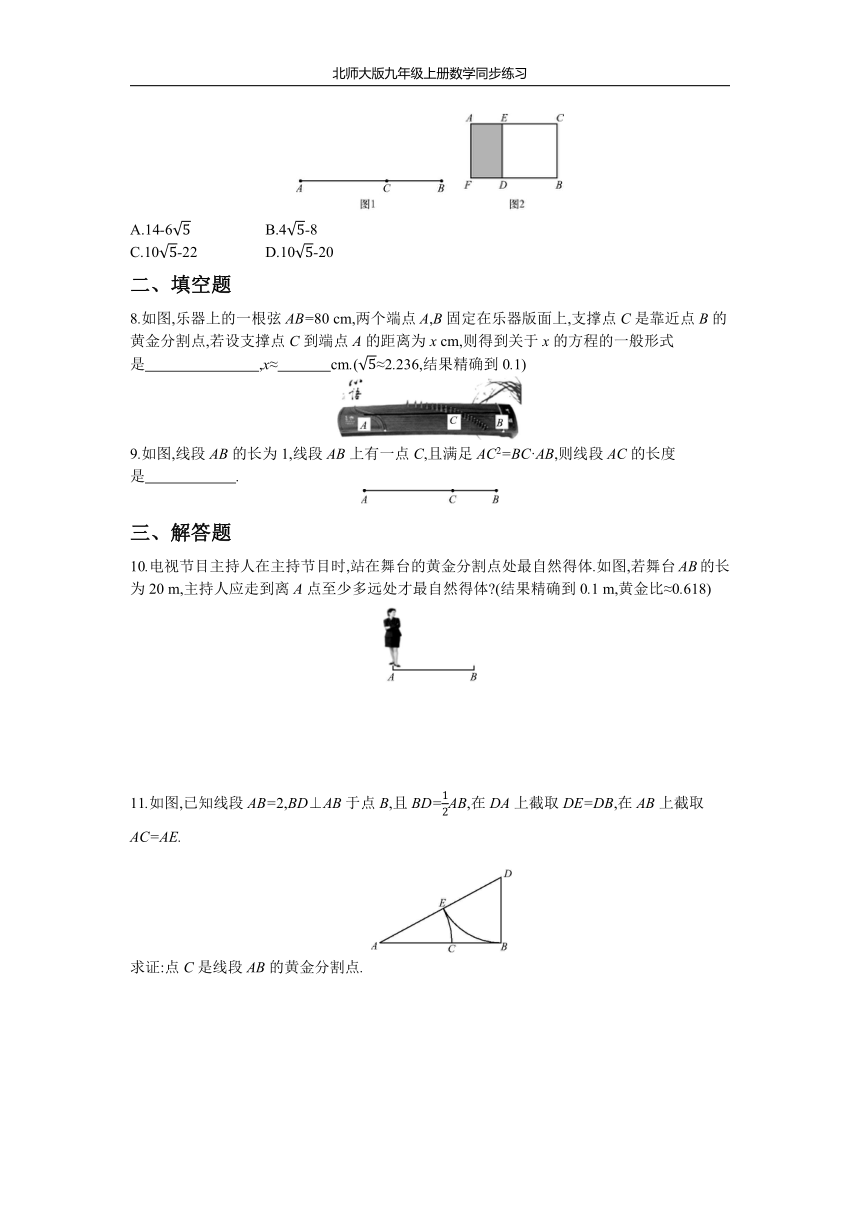
7.如图1,AB=2,点C在线段AB上,且满足.如图2,以图1中的AC,BC长为边构建矩形ACBF,以CB长为边构建正方形CBDE,则矩形AEDF的面积为
( )
A.14-6
B.4-8
C.10-22
D.10-20
二、填空题
8.如图,乐器上的一根弦AB=80
cm,两个端点A,B固定在乐器版面上,支撑点C是靠近点B的黄金分割点,若设支撑点C到端点A的距离为x
cm,则得到关于x的方程的一般形式是
,x≈
cm.(≈2.236,结果精确到0.1)?
9.如图,线段AB的长为1,线段AB上有一点C,且满足AC2=BC·AB,则线段AC的长度是
.?
三、解答题
10.电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20
m,主持人应走到离A点至少多远处才最自然得体?(结果精确到0.1
m,黄金比≈0.618)
11.如图,已知线段AB=2,BD⊥AB于点B,且BD=AB,在DA上截取DE=DB,在AB上截取AC=AE.
求证:点C是线段AB的黄金分割点.
12.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,试说明D是线段AC的黄金分割点.
13.已知点D是线段AB的黄金分割点,且AD>BD.
(1)若AB=10
cm,则AD=
;?
(2)如图,请用尺规作出以AD为底的黄金三角形;(黄金三角形是一个等腰三角形,且底与腰的长度比为黄金比)
(3)证明你画出的三角形是黄金三角形.
14.如图,要设计一座高为2米的人体雕像AB,使雕像的上部AC(腰点C以上)与下部(腰点C以下)的高度之比等于下部BC与全部AB(身高)的高度之比,则雕像的下部BC的长应设计为多少米?
15.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果(S1>S2),那么称直线l为该图形的黄金分割线.
(1)如图2,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是不是AB边上的黄金分割点?(直接写出结论,不必证明)
(2)若△ABC在(1)的条件下,如图3,请问直线CD是不是△ABC的黄金分割线?并证明你的结论.
(3)如图4,在直角梯形ABCD中,∠ADC=∠BCD=90°,对角线AC,BD相交于点F,延长AB,DC交于点E,连接EF并延长分别交梯形上、下底于G,H两点,请问直线GH是不是直角梯形ABCD的黄金分割线?并证明你的结论.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
答案
A
C
B
B
B
C
C
二、填空题
8. x2+80x-6400=0 49.4 ?
9.?
三、解答题
10.解:设主持人应走到离A点至少x
m处才最自然得体.
根据黄金比,得x=20×(1-0.618)≈7.6.
∵黄金分割点有2个,∴x=20-7.6=12.4.
∵7.6<12.4,∴x应取7.6.
答:主持人应走到离A点至少7.6
m处才最自然得体.
11.
证明:∵AB=2,BD=AB,∴BD=1.
∵BD⊥AB于点B,∴AD=,
∴AE=AD-DE=-1,∴AC=AE=-1,
∴AC=AB,
∴点C是线段AB的黄金分割点.
12.在△ABC中,AB=AC,∠A=36°,
所以∠ABC=∠C==72°,
因为BD平分∠ABC,
所以∠1=∠2=36°,
所以∠2=∠A,
所以△ABC∽△BCD,
所以.
因为∠1=∠A=36°,
所以AD=BD.
因为∠C=72°,∠BDC=180°-∠2-∠C=72°,
所以BC=BD,
所以BC=AD,
所以,
所以点D是线段AC的黄金分割点.
13.
(1) (5-5)
cm
解:(2)分别以点A,D为圆心,以AB的长为半径作弧,两弧交于点B',连接B'D,AB',则△AB'D即为所求.图略.
(3)∵点D是线段AB的黄金分割点,
∴底边AD=AB,∴△AB'D是黄金三角形.
14.解:设下部应设计为x米,则上部的长度为(2-x)米,
根据题意,得,整理得x2+2x-4=0,
解得x1=-1+,x2=-1-(舍去),
所以雕像的下部应设计为(-1+)米.
15.解:(1)D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.
设△ABC的边AB上的高为h,则S△ADC=AD·h,S△DBC=BD·h,S△ABC=AB·h,
∴S△ADC∶S△ABC=AD∶AB,S△DBC∶S△ADC=BD∶AD.
由(1)知D是AB的黄金分割点,
∴,∴S△ADC∶S△ABC=S△DBC∶S△ADC,
∴直线CD是△ABC的黄金分割线.
(3)直线GH不是直角梯形ABCD的黄金分割线.
∵BC∥AD,∴△EBG∽△EAH,△EGC∽△EHD,
∴, ①
. ②
由①②得,即. ③
同理,得△BGF∽△DHF,△CGF∽△AHF,
∴,即. ④
由③④得,∴AH=HD,∴BG=GC,
∴梯形ABGH与梯形GCDH的上、下底分别相等,高也相等,∴S梯形ABGH=S梯形GCDH=S梯形ABCD,
∴直线GH不是直角梯形ABCD的黄金分割线.
第4课时 黄金分割
一、选择题
1.已知点C是线段AB的黄金分割点,且AC>BC,则下列等式中成立的是
( )
A.AC2=BC·AB
B.AC2=2AB·BC
C.AB2=AC·BC
D.BC2=AC·AB
2.如图,已知线段AB=60,AD=13,DE=17,EF=7,请问在D,E,F三点中,哪一点最接近线段AB的黄金分割点
( )
A.D点
B.E点
C.F点
D.D点或F点
3.已知点P是线段AB的黄金分割点,AP>BP.记以AP为一边的正方形的面积为S1,以BP,AB的长为邻边的矩形的面积为S2,则
( )
A.S1>S2
B.S1=S2
C.S1
4.如图所示,扇子的圆心角为α,余下扇形的圆心角为β,α与β的比通常按黄金比来设计,这样的扇子比较美观.若取黄金比为0.6,则α为
( )
A.216°
B.135°
C.120°
D.108°
5.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是≈0.618,称为黄金比例.如图,著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉与咽喉至肚脐的长度之比也是.若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为26
cm,则其身高可能是
( )
A.165
cm
B.178
cm
C.185
cm
D.190
cm
6.人以肚脐为界,下身与身高比例符合“黄金分割”比例,在人的视觉里看,是最完美的比例,身高为170
cm的人,满足“黄金分割”比例的腿长约为
( )
A.100
cm
B.104
cm
C.105
cm
D.112
cm
7.如图1,AB=2,点C在线段AB上,且满足.如图2,以图1中的AC,BC长为边构建矩形ACBF,以CB长为边构建正方形CBDE,则矩形AEDF的面积为
( )
A.14-6
B.4-8
C.10-22
D.10-20
二、填空题
8.如图,乐器上的一根弦AB=80
cm,两个端点A,B固定在乐器版面上,支撑点C是靠近点B的黄金分割点,若设支撑点C到端点A的距离为x
cm,则得到关于x的方程的一般形式是
,x≈
cm.(≈2.236,结果精确到0.1)?
9.如图,线段AB的长为1,线段AB上有一点C,且满足AC2=BC·AB,则线段AC的长度是
.?
三、解答题
10.电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20
m,主持人应走到离A点至少多远处才最自然得体?(结果精确到0.1
m,黄金比≈0.618)
11.如图,已知线段AB=2,BD⊥AB于点B,且BD=AB,在DA上截取DE=DB,在AB上截取AC=AE.
求证:点C是线段AB的黄金分割点.
12.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,试说明D是线段AC的黄金分割点.
13.已知点D是线段AB的黄金分割点,且AD>BD.
(1)若AB=10
cm,则AD=
;?
(2)如图,请用尺规作出以AD为底的黄金三角形;(黄金三角形是一个等腰三角形,且底与腰的长度比为黄金比)
(3)证明你画出的三角形是黄金三角形.
14.如图,要设计一座高为2米的人体雕像AB,使雕像的上部AC(腰点C以上)与下部(腰点C以下)的高度之比等于下部BC与全部AB(身高)的高度之比,则雕像的下部BC的长应设计为多少米?
15.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果(S1>S2),那么称直线l为该图形的黄金分割线.
(1)如图2,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是不是AB边上的黄金分割点?(直接写出结论,不必证明)
(2)若△ABC在(1)的条件下,如图3,请问直线CD是不是△ABC的黄金分割线?并证明你的结论.
(3)如图4,在直角梯形ABCD中,∠ADC=∠BCD=90°,对角线AC,BD相交于点F,延长AB,DC交于点E,连接EF并延长分别交梯形上、下底于G,H两点,请问直线GH是不是直角梯形ABCD的黄金分割线?并证明你的结论.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
答案
A
C
B
B
B
C
C
二、填空题
8. x2+80x-6400=0 49.4 ?
9.?
三、解答题
10.解:设主持人应走到离A点至少x
m处才最自然得体.
根据黄金比,得x=20×(1-0.618)≈7.6.
∵黄金分割点有2个,∴x=20-7.6=12.4.
∵7.6<12.4,∴x应取7.6.
答:主持人应走到离A点至少7.6
m处才最自然得体.
11.
证明:∵AB=2,BD=AB,∴BD=1.
∵BD⊥AB于点B,∴AD=,
∴AE=AD-DE=-1,∴AC=AE=-1,
∴AC=AB,
∴点C是线段AB的黄金分割点.
12.在△ABC中,AB=AC,∠A=36°,
所以∠ABC=∠C==72°,
因为BD平分∠ABC,
所以∠1=∠2=36°,
所以∠2=∠A,
所以△ABC∽△BCD,
所以.
因为∠1=∠A=36°,
所以AD=BD.
因为∠C=72°,∠BDC=180°-∠2-∠C=72°,
所以BC=BD,
所以BC=AD,
所以,
所以点D是线段AC的黄金分割点.
13.
(1) (5-5)
cm
解:(2)分别以点A,D为圆心,以AB的长为半径作弧,两弧交于点B',连接B'D,AB',则△AB'D即为所求.图略.
(3)∵点D是线段AB的黄金分割点,
∴底边AD=AB,∴△AB'D是黄金三角形.
14.解:设下部应设计为x米,则上部的长度为(2-x)米,
根据题意,得,整理得x2+2x-4=0,
解得x1=-1+,x2=-1-(舍去),
所以雕像的下部应设计为(-1+)米.
15.解:(1)D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.
设△ABC的边AB上的高为h,则S△ADC=AD·h,S△DBC=BD·h,S△ABC=AB·h,
∴S△ADC∶S△ABC=AD∶AB,S△DBC∶S△ADC=BD∶AD.
由(1)知D是AB的黄金分割点,
∴,∴S△ADC∶S△ABC=S△DBC∶S△ADC,
∴直线CD是△ABC的黄金分割线.
(3)直线GH不是直角梯形ABCD的黄金分割线.
∵BC∥AD,∴△EBG∽△EAH,△EGC∽△EHD,
∴, ①
. ②
由①②得,即. ③
同理,得△BGF∽△DHF,△CGF∽△AHF,
∴,即. ④
由③④得,∴AH=HD,∴BG=GC,
∴梯形ABGH与梯形GCDH的上、下底分别相等,高也相等,∴S梯形ABGH=S梯形GCDH=S梯形ABCD,
∴直线GH不是直角梯形ABCD的黄金分割线.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
