北师大版九年级上册数学同步练习4.6 利用相似三角形测高(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学同步练习4.6 利用相似三角形测高(Word版 含答案 ) |
|
|
| 格式 | zip | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 00:00:00 | ||
图片预览



文档简介
北师大版九年级上册数学同步练习
4.6 利用相似三角形测高
一、选择题
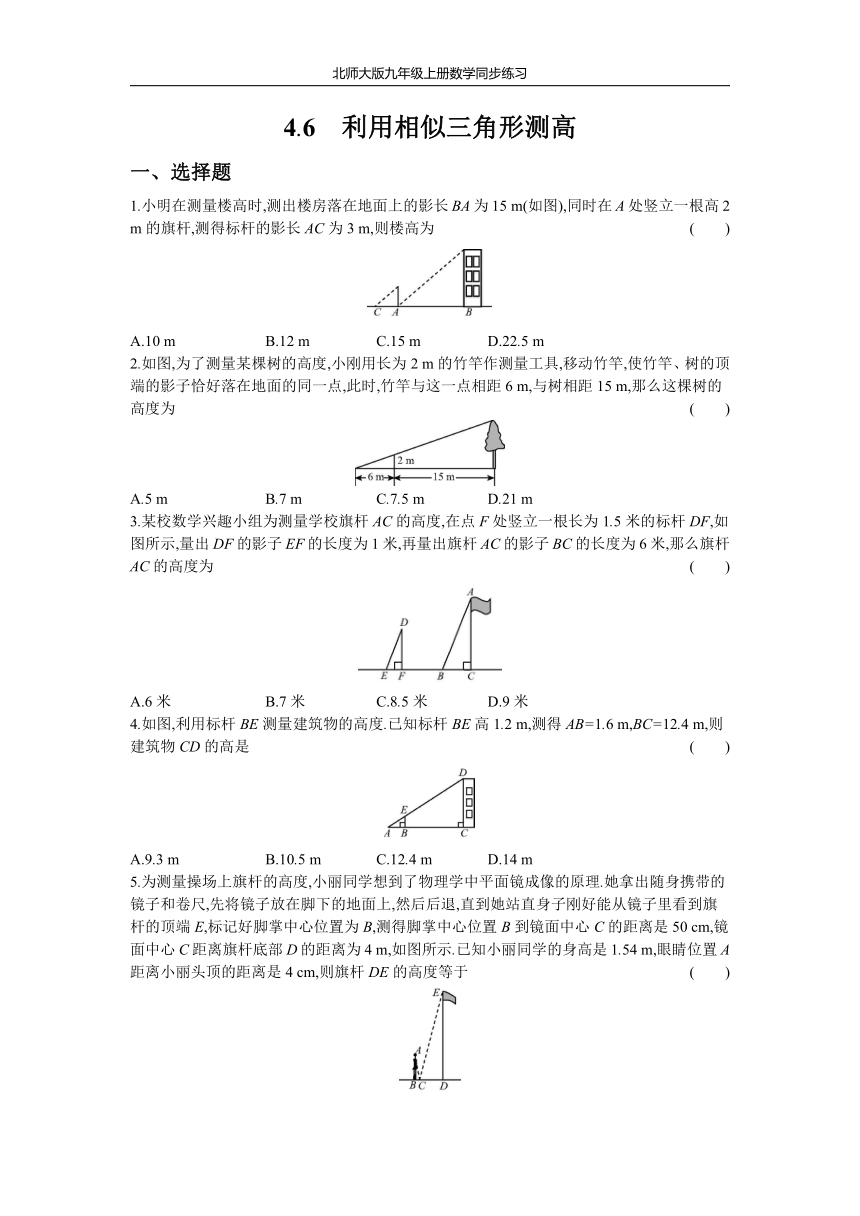
1.小明在测量楼高时,测出楼房落在地面上的影长BA为15
m(如图),同时在A处竖立一根高2
m的旗杆,测得标杆的影长AC为3
m,则楼高为
( )
A.10
m
B.12
m
C.15
m
D.22.5
m
2.如图,为了测量某棵树的高度,小刚用长为2
m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6
m,与树相距15
m,那么这棵树的高度为
( )
A.5
m
B.7
m
C.7.5
m
D.21
m
3.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为
( )
A.6米
B.7米
C.8.5米
D.9米
4.如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2
m,测得AB=1.6
m,BC=12.4
m,则建筑物CD的高是
( )
A.9.3
m
B.10.5
m
C.12.4
m
D.14
m
5.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50
cm,镜面中心C距离旗杆底部D的距离为4
m,如图所示.已知小丽同学的身高是1.54
m,眼睛位置A距离小丽头顶的距离是4
cm,则旗杆DE的高度等于
( )
A.10
m
B.12
m
C.12.4
m
D.12.32
m
6.如图,小明为了测量某凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高EF=1.6米,则凉亭的高度AB约为
( )
A.8.5米
B.9米
C.9.5米
D.10米
7.如图所示,某超市在
一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2
m)乘电梯刚好安全通过,请你根据图中的数据回答,两层楼之间的高约为
( )
A.5.5
m
B.6.2
m
C.11
m
D.2.2
m
8.我国古代数学《九章算术》中,有个“井深几何”问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺=10寸),问井深几何?其意思如图所示,则井深BD的长为
( )
A.12尺
B.56尺5寸
C.57尺5寸
D.62尺5寸
二、填空题
9.在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一只点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如图1).如图2,如果火焰AB的高度是2
cm,倒立的像A'B'的高度为5
cm,蜡烛火焰根B到小孔O的距离为4
cm,则火焰像的根B'到小孔O的距离是
cm.?
10.如图,某一时刻一根2米长的竹竿EF的影长GE为1.2米,此时,小红测得一棵被风吹斜的杨树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB等于
米.?
11.我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走40步后刚好有一棵树木,若从西门往正西方向走810步后正好看到树木,则正方形城池的边长为
步.?
三、解答题
12.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的一侧选点A,B,D,使得AB⊥AO,BD⊥AB,然后确定DO和AB的交点C,测得AC=120
m,CB=60
m,BD=50
m,你能帮助他们算出峡谷的宽OA吗?
13.如图,小明欲测量一座古塔的高度,他拿来一根竹竿竖直插在地面上,然后自己退后,使眼睛通过竹竿的顶端刚好看到塔顶,若小明眼睛离地面1.6
m,竹竿顶端离地面2.4
m,小明到竹竿的距离DF=2
m,竹竿到塔底的距离DB=33
m,求这座古塔的高度.
14.如图,小华在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离EB=20米,镜子与小华的距离ED=2米,小华刚好从镜子中看到铁塔顶端点A.已知小华的眼睛距离地面的高度CD=1.5米,则铁塔AB的高度是多少米?
15.要测量旗杆CD的高,在B处立标杆AB,人在F处,眼睛E、标杆顶A、
旗杆顶C在一条直线上.已知AB=2.5
m,BD=3.6
m,FB=2.2
m,EF=1.5
m.求旗杆CD的高度.(精确到0.1
m)
16.如图,梯子AB靠在墙壁上,梯子的底端B距离墙60
cm,梯子上的点D距离墙40
cm,BD长55
cm,求梯子AB的长.
17.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一条直线上,已知DE=1米,EF=0.5米,测点D到地面的距离DG=3米,到旗杆的水平距离DC=40米,求旗杆的高度.
18.如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC=2
m,BD=2.1
m.如果小明眼睛距地面高度BF,DG为1.6
m,试确定楼的高度OE.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
B
D
B
B
A
A
C
二、填空题
9. 10
10. 12
11. 360
三、解答题
12.∵OA⊥AB,BD⊥AB,
∴OA∥BD,
∴△AOC∽△BDC,
∴,即,
∴OA=100.
答:这个峡谷的宽度是100
m.
13.作EH⊥AB于点H,交CD于点G.
∵CD⊥BF,AB⊥BF,∴CD∥AB,
∴△EGC∽△EHA,∴.
又∵CG=2.4-1.6=0.8,,
∴AH=×0.8=14,
又∵BH=EF=1.6,
∴AB=AH+BH=15.6.
答:古塔的高度为15.6
m.
14.根据反射角等于入射角可得∠1=∠2,
∵∠1+∠AEB=90°,∠2+∠CED=90°,
∴∠AEB=∠CED.
又∵AB⊥BD,CD⊥BD,
∴∠ABE=∠CDE=90°,
∴△ABE∽△CDE,
∴,
又∵CD=1.5,EB=20,ED=2,
∴,AB=15.
即铁塔的高度为15米.
15.解:过点E作EM⊥CD,分别交CD,AB于点M,N.
∴AN=AB-EF=2.5-1.5=1
m,EM=FD=FB+BD=2.2+3.6=5.8
m.
由△EAN∽△ECM,得,即,
解得CM≈2.6
m,
∴CD=CM+MD≈2.6+1.5=4.1
m.
答:旗杆的高度约为4.1
m.
16.解:∵DE⊥AC,BC⊥AC,
∴∠AED=∠ACB=90°.
又∵∠EAD=∠CAB,
∴△AED∽△ACB,∴.
∵AD=AB-BD,BD=55
cm,DE=40
cm,BC=60
cm,
∴,解得AB=165
cm.
答:梯子的长度为165
cm.
17.解:∵∠ADC=∠FDE,∠ACD=∠FED=90°,
∴△ACD∽△FED,∴,即,解得AC=20.
∵AB⊥BG,DG⊥BG,DC⊥AB,
∴∠ABG=∠BGD=∠DCB=90°,
∴四边形BGDC是矩形,∴BC=DG=3,
∴AB=AC+BC=20+3=23(米).
答:旗杆AB的高度是23米.
18.解:令OE=a,AO=b,CB=x,
则由△GDC∽△EOC得,即,
整理得3.2+1.6b=2.1a-ax, ①
由△FBA∽△EOA得,即,
整理得1.6b=2a-ax, ②
将②代入①,得3.2+2a-ax=2.1a-ax,
∴a=32,即OE=32.
答:楼的高度OE为32米.
4.6 利用相似三角形测高
一、选择题
1.小明在测量楼高时,测出楼房落在地面上的影长BA为15
m(如图),同时在A处竖立一根高2
m的旗杆,测得标杆的影长AC为3
m,则楼高为
( )
A.10
m
B.12
m
C.15
m
D.22.5
m
2.如图,为了测量某棵树的高度,小刚用长为2
m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6
m,与树相距15
m,那么这棵树的高度为
( )
A.5
m
B.7
m
C.7.5
m
D.21
m
3.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为
( )
A.6米
B.7米
C.8.5米
D.9米
4.如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2
m,测得AB=1.6
m,BC=12.4
m,则建筑物CD的高是
( )
A.9.3
m
B.10.5
m
C.12.4
m
D.14
m
5.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50
cm,镜面中心C距离旗杆底部D的距离为4
m,如图所示.已知小丽同学的身高是1.54
m,眼睛位置A距离小丽头顶的距离是4
cm,则旗杆DE的高度等于
( )
A.10
m
B.12
m
C.12.4
m
D.12.32
m
6.如图,小明为了测量某凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高EF=1.6米,则凉亭的高度AB约为
( )
A.8.5米
B.9米
C.9.5米
D.10米
7.如图所示,某超市在
一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2
m)乘电梯刚好安全通过,请你根据图中的数据回答,两层楼之间的高约为
( )
A.5.5
m
B.6.2
m
C.11
m
D.2.2
m
8.我国古代数学《九章算术》中,有个“井深几何”问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺=10寸),问井深几何?其意思如图所示,则井深BD的长为
( )
A.12尺
B.56尺5寸
C.57尺5寸
D.62尺5寸
二、填空题
9.在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一只点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如图1).如图2,如果火焰AB的高度是2
cm,倒立的像A'B'的高度为5
cm,蜡烛火焰根B到小孔O的距离为4
cm,则火焰像的根B'到小孔O的距离是
cm.?
10.如图,某一时刻一根2米长的竹竿EF的影长GE为1.2米,此时,小红测得一棵被风吹斜的杨树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB等于
米.?
11.我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走40步后刚好有一棵树木,若从西门往正西方向走810步后正好看到树木,则正方形城池的边长为
步.?
三、解答题
12.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的一侧选点A,B,D,使得AB⊥AO,BD⊥AB,然后确定DO和AB的交点C,测得AC=120
m,CB=60
m,BD=50
m,你能帮助他们算出峡谷的宽OA吗?
13.如图,小明欲测量一座古塔的高度,他拿来一根竹竿竖直插在地面上,然后自己退后,使眼睛通过竹竿的顶端刚好看到塔顶,若小明眼睛离地面1.6
m,竹竿顶端离地面2.4
m,小明到竹竿的距离DF=2
m,竹竿到塔底的距离DB=33
m,求这座古塔的高度.
14.如图,小华在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离EB=20米,镜子与小华的距离ED=2米,小华刚好从镜子中看到铁塔顶端点A.已知小华的眼睛距离地面的高度CD=1.5米,则铁塔AB的高度是多少米?
15.要测量旗杆CD的高,在B处立标杆AB,人在F处,眼睛E、标杆顶A、
旗杆顶C在一条直线上.已知AB=2.5
m,BD=3.6
m,FB=2.2
m,EF=1.5
m.求旗杆CD的高度.(精确到0.1
m)
16.如图,梯子AB靠在墙壁上,梯子的底端B距离墙60
cm,梯子上的点D距离墙40
cm,BD长55
cm,求梯子AB的长.
17.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一条直线上,已知DE=1米,EF=0.5米,测点D到地面的距离DG=3米,到旗杆的水平距离DC=40米,求旗杆的高度.
18.如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC=2
m,BD=2.1
m.如果小明眼睛距地面高度BF,DG为1.6
m,试确定楼的高度OE.
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
B
D
B
B
A
A
C
二、填空题
9. 10
10. 12
11. 360
三、解答题
12.∵OA⊥AB,BD⊥AB,
∴OA∥BD,
∴△AOC∽△BDC,
∴,即,
∴OA=100.
答:这个峡谷的宽度是100
m.
13.作EH⊥AB于点H,交CD于点G.
∵CD⊥BF,AB⊥BF,∴CD∥AB,
∴△EGC∽△EHA,∴.
又∵CG=2.4-1.6=0.8,,
∴AH=×0.8=14,
又∵BH=EF=1.6,
∴AB=AH+BH=15.6.
答:古塔的高度为15.6
m.
14.根据反射角等于入射角可得∠1=∠2,
∵∠1+∠AEB=90°,∠2+∠CED=90°,
∴∠AEB=∠CED.
又∵AB⊥BD,CD⊥BD,
∴∠ABE=∠CDE=90°,
∴△ABE∽△CDE,
∴,
又∵CD=1.5,EB=20,ED=2,
∴,AB=15.
即铁塔的高度为15米.
15.解:过点E作EM⊥CD,分别交CD,AB于点M,N.
∴AN=AB-EF=2.5-1.5=1
m,EM=FD=FB+BD=2.2+3.6=5.8
m.
由△EAN∽△ECM,得,即,
解得CM≈2.6
m,
∴CD=CM+MD≈2.6+1.5=4.1
m.
答:旗杆的高度约为4.1
m.
16.解:∵DE⊥AC,BC⊥AC,
∴∠AED=∠ACB=90°.
又∵∠EAD=∠CAB,
∴△AED∽△ACB,∴.
∵AD=AB-BD,BD=55
cm,DE=40
cm,BC=60
cm,
∴,解得AB=165
cm.
答:梯子的长度为165
cm.
17.解:∵∠ADC=∠FDE,∠ACD=∠FED=90°,
∴△ACD∽△FED,∴,即,解得AC=20.
∵AB⊥BG,DG⊥BG,DC⊥AB,
∴∠ABG=∠BGD=∠DCB=90°,
∴四边形BGDC是矩形,∴BC=DG=3,
∴AB=AC+BC=20+3=23(米).
答:旗杆AB的高度是23米.
18.解:令OE=a,AO=b,CB=x,
则由△GDC∽△EOC得,即,
整理得3.2+1.6b=2.1a-ax, ①
由△FBA∽△EOA得,即,
整理得1.6b=2a-ax, ②
将②代入①,得3.2+2a-ax=2.1a-ax,
∴a=32,即OE=32.
答:楼的高度OE为32米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
