北师大版九年级上册数学同步练习4.7 第1课时 相似三角形中特殊线段的性质(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学同步练习4.7 第1课时 相似三角形中特殊线段的性质(Word版 含答案 ) |  | |
| 格式 | zip | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 13:11:25 | ||
图片预览

文档简介
北师大版九年级上册数学同步练习
4.7 相似三角形的性质
第1课时 相似三角形中特殊线段的性质
一、选择题
1.如果两个相似三角形对应边的比为4∶5,那么它们对应中线的比是
( )
A.2∶
B.2∶5
C.4∶5
D.16∶25
2.若△ABC∽△DEF,且AB=5,DE=3,则△ABC与△DEF的边BC和EF上的高的比是
( )
A.5∶3
B.3∶5
C.25∶9
D.9∶25
3.已知△ABC∽△DEF,若AM,DN分别是两个三角形的角平分线,且,则△DEF与△ABC的相似比是
( )
A.9∶4
B.4∶9
C.3∶2
D.2∶3
4.如图,在?ABCD中,E是AD边上的中点,连接BE并延长交CD的延长线于点F,则△EDF与△BCF的对应角平分线的比为
( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
5.如图,物理课上张明做小孔成像实验,已知蜡烛与成像板之间的距离BB'为36
cm,要使烛焰的像A'B'是烛焰AB的2倍,则蜡烛与成像板之间的小孔纸板的距离OB应为
( )
A.12
cm
B.24
cm
C.18
cm
D.9
cm
6.两个相似三角形的对应角平分线之比为3∶4,则其相应中线之比为
( )
A.∶2
B.3∶4
C.9∶16
D.不能确定
7.学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5
m,OA的长为3
m,点C到AB的距离为0.3
m,支柱OE的高为0.6
m,则栏杆D端离地面的距离为
( )
A.1.2
m
B.1.8
m
C.2.4
m
D.3
m
8.已知△ABC∽△A'B'C'且相似比为,△A'B'C'∽△A″B″C″且相似比为,则△ABC与△A″B″C″的相似比为
( )
A.
B.
C.
D.
二、填空题
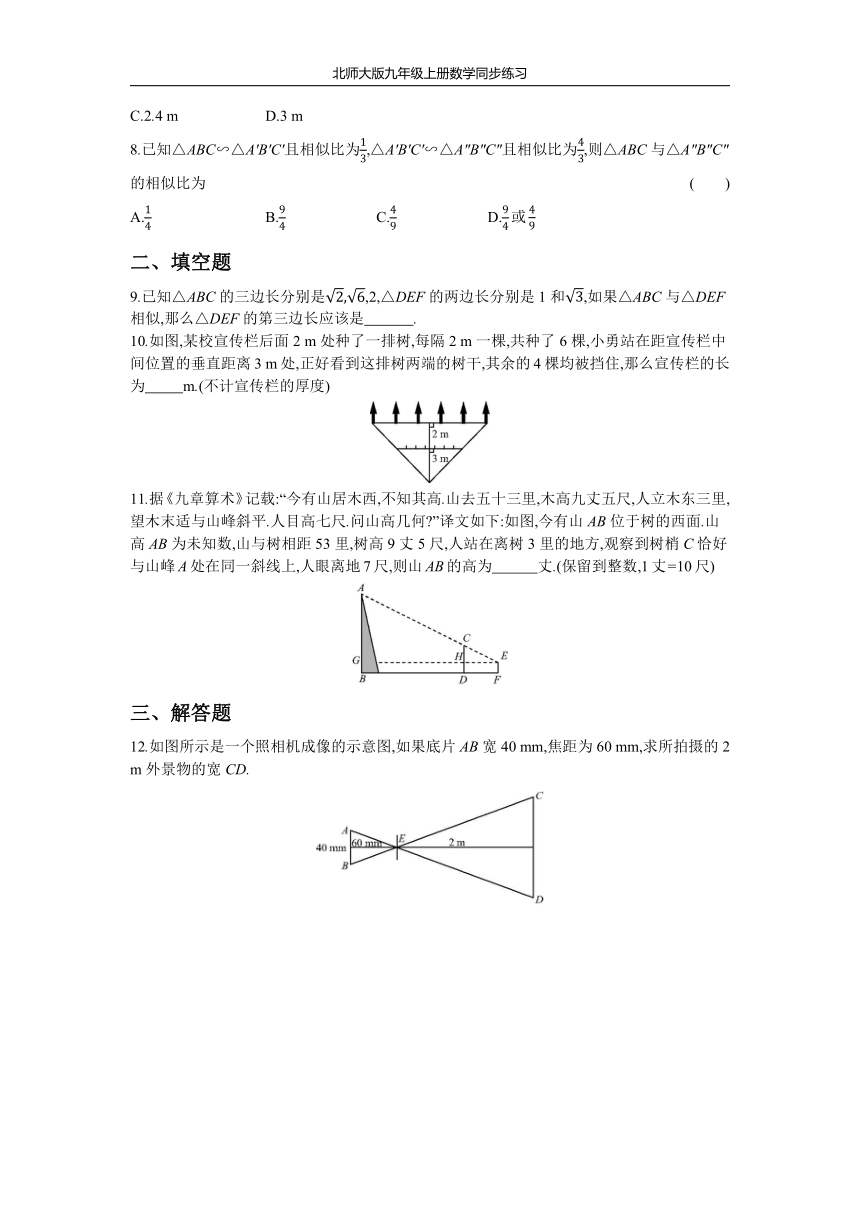
9.已知△ABC的三边长分别是,2,△DEF的两边长分别是1和,如果△ABC与△DEF相似,那么△DEF的第三边长应该是?
.?
10.如图,某校宣传栏后面2
m处种了一排树,每隔2
m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3
m处,正好看到这排树两端的树干,其余的4棵均被挡住,那么宣传栏的长为
m.(不计宣传栏的厚度)?
11.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为
丈.(保留到整数,1丈=10尺)?
三、解答题
12.如图所示是一个照相机成像的示意图,如果底片AB宽40
mm,焦距为60
mm,求所拍摄的2
m外景物的宽CD.
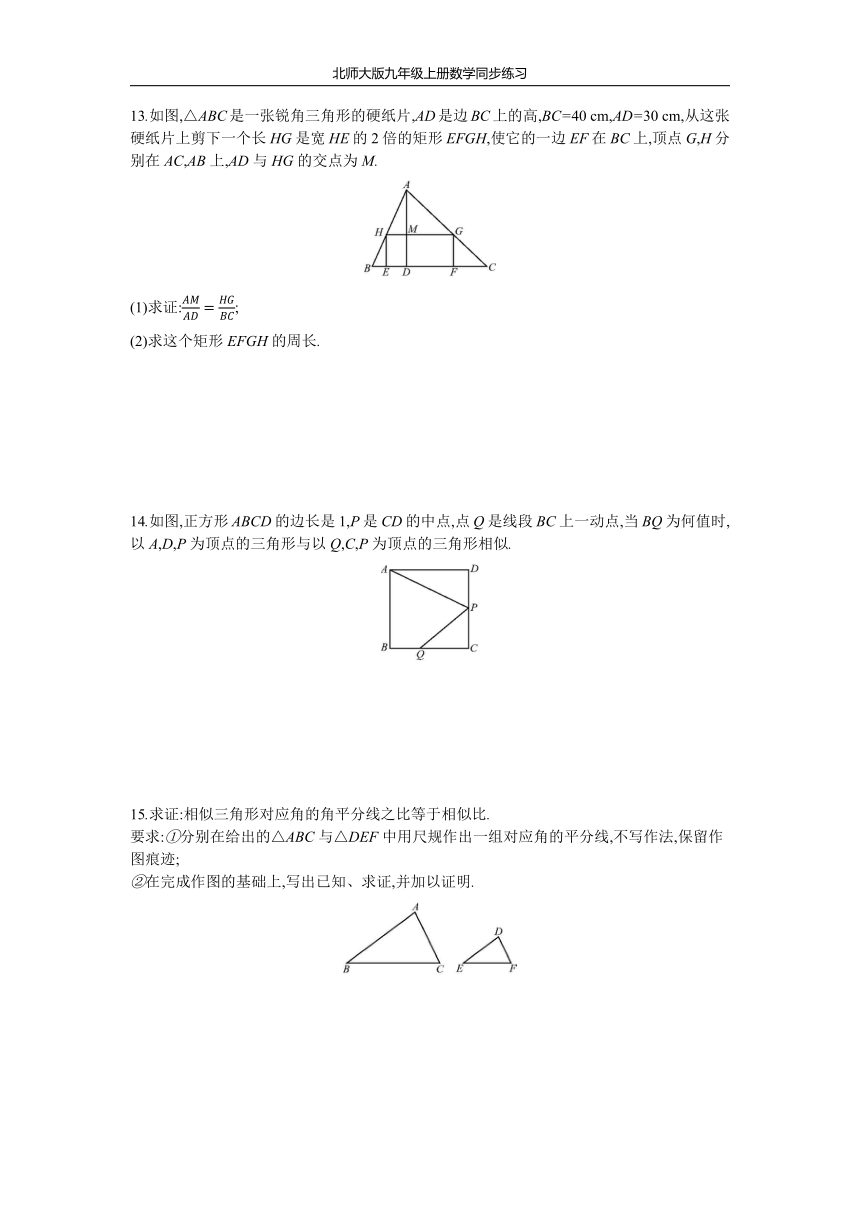
13.如图,△ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40
cm,AD=30
cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:;
(2)求这个矩形EFGH的周长.
14.如图,正方形ABCD的边长是1,P是CD的中点,点Q是线段BC上一动点,当BQ为何值时,以A,D,P为顶点的三角形与以Q,C,P为顶点的三角形相似.
15.求证:相似三角形对应角的角平分线之比等于相似比.
要求:①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
16.一块直角三角板的一条直角边AB的长为1.5
m,面积为1.5
m2,要把它加工成一个面积尽可能大的正方形桌面,甲,乙两位同学的加工方法分别如图1,2所示,请你用学过的知识说明哪位同学的加工方法更好.(加工损耗忽略不计,计算结果中的分数可保留)
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
C
A
B
A
A
B
C
C
二、填空题
9.?
10. 6
11. 165
三、解答题
12.解:由题可知△ABE∽△DCE,
∴,解得CD=
m.
答:所拍摄的2
m外景物的宽CD为
m.
13.
(1)∵四边形EFGH为矩形,
∴EF∥GH,∴∠AHG=∠ABC.
又∵∠HAG=∠BAC,∴△AHG∽△ABC.
又∵AD⊥BC,∴AM⊥HG,∴.
(2)由(1)得,设HE=x,则HG=2x,
∵AD⊥BC,∴DM=HE,
∴AM=AD-DM=AD-HE=30-x,
可得,
解得x=12,2x=24,
所以矩形EFGH的周长为2×(12+24)=72(cm).
14.∵正方形ABCD的边长是1,P是CD的中点,∴PD=PC=.
①当DP与PC是对应边时,,即,
解得CQ=1,∴BQ=BC-CQ=1-1=0;
②当DP与CQ是对应边时,,即,解得CQ=,∴BQ=BC-CQ=1-.
综上所述,BQ的长度是0或时,以A,D,P为顶点的三角形与以Q,C,P为顶点的三角形相似.
15.解:①如图所示,AG,DH分别是∠BAC与∠EDF的角平分线.
②已知:如图,△ABC∽△DEF,=k,AG,DH分别是∠BAC与∠EDF的角平分线.
求证:=k.
证明:∵AG,DH分别是△ABC与△DEF的角平分线,
∴∠BAG=∠BAC,∠EDH=∠EDF.
∵△ABC∽△DEF,
∴∠BAC=∠EDF,∠B=∠E,
∴∠BAG=∠EDH,
∴△ABG∽△DEH,∴=k.
16.解:由AB=1.5
m,S△ABC=1.5
m2,得BC=2
m.
在题图1中,设甲同学加工的正方形桌面边长为x
m.
∵DE∥AB,∴Rt△CDE∽Rt△CBA,
∴,即,解得x=.
在题图2中,过点B作BH⊥AC,交AC于点H,交DE于点P.
AC==2.5
m,
BH==1.2
m.
设乙同学加工的桌面边长为y
m.
∵DE∥AC,∴△BDE∽△BAC,
∴,即,解得y=.
∵,即x>y,∴x2>y2,
∴甲同学的加工方法更好.
4.7 相似三角形的性质
第1课时 相似三角形中特殊线段的性质
一、选择题
1.如果两个相似三角形对应边的比为4∶5,那么它们对应中线的比是
( )
A.2∶
B.2∶5
C.4∶5
D.16∶25
2.若△ABC∽△DEF,且AB=5,DE=3,则△ABC与△DEF的边BC和EF上的高的比是
( )
A.5∶3
B.3∶5
C.25∶9
D.9∶25
3.已知△ABC∽△DEF,若AM,DN分别是两个三角形的角平分线,且,则△DEF与△ABC的相似比是
( )
A.9∶4
B.4∶9
C.3∶2
D.2∶3
4.如图,在?ABCD中,E是AD边上的中点,连接BE并延长交CD的延长线于点F,则△EDF与△BCF的对应角平分线的比为
( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
5.如图,物理课上张明做小孔成像实验,已知蜡烛与成像板之间的距离BB'为36
cm,要使烛焰的像A'B'是烛焰AB的2倍,则蜡烛与成像板之间的小孔纸板的距离OB应为
( )
A.12
cm
B.24
cm
C.18
cm
D.9
cm
6.两个相似三角形的对应角平分线之比为3∶4,则其相应中线之比为
( )
A.∶2
B.3∶4
C.9∶16
D.不能确定
7.学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5
m,OA的长为3
m,点C到AB的距离为0.3
m,支柱OE的高为0.6
m,则栏杆D端离地面的距离为
( )
A.1.2
m
B.1.8
m
C.2.4
m
D.3
m
8.已知△ABC∽△A'B'C'且相似比为,△A'B'C'∽△A″B″C″且相似比为,则△ABC与△A″B″C″的相似比为
( )
A.
B.
C.
D.
二、填空题
9.已知△ABC的三边长分别是,2,△DEF的两边长分别是1和,如果△ABC与△DEF相似,那么△DEF的第三边长应该是?
.?
10.如图,某校宣传栏后面2
m处种了一排树,每隔2
m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3
m处,正好看到这排树两端的树干,其余的4棵均被挡住,那么宣传栏的长为
m.(不计宣传栏的厚度)?
11.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为
丈.(保留到整数,1丈=10尺)?
三、解答题
12.如图所示是一个照相机成像的示意图,如果底片AB宽40
mm,焦距为60
mm,求所拍摄的2
m外景物的宽CD.
13.如图,△ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40
cm,AD=30
cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:;
(2)求这个矩形EFGH的周长.
14.如图,正方形ABCD的边长是1,P是CD的中点,点Q是线段BC上一动点,当BQ为何值时,以A,D,P为顶点的三角形与以Q,C,P为顶点的三角形相似.
15.求证:相似三角形对应角的角平分线之比等于相似比.
要求:①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
16.一块直角三角板的一条直角边AB的长为1.5
m,面积为1.5
m2,要把它加工成一个面积尽可能大的正方形桌面,甲,乙两位同学的加工方法分别如图1,2所示,请你用学过的知识说明哪位同学的加工方法更好.(加工损耗忽略不计,计算结果中的分数可保留)
参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
C
A
B
A
A
B
C
C
二、填空题
9.?
10. 6
11. 165
三、解答题
12.解:由题可知△ABE∽△DCE,
∴,解得CD=
m.
答:所拍摄的2
m外景物的宽CD为
m.
13.
(1)∵四边形EFGH为矩形,
∴EF∥GH,∴∠AHG=∠ABC.
又∵∠HAG=∠BAC,∴△AHG∽△ABC.
又∵AD⊥BC,∴AM⊥HG,∴.
(2)由(1)得,设HE=x,则HG=2x,
∵AD⊥BC,∴DM=HE,
∴AM=AD-DM=AD-HE=30-x,
可得,
解得x=12,2x=24,
所以矩形EFGH的周长为2×(12+24)=72(cm).
14.∵正方形ABCD的边长是1,P是CD的中点,∴PD=PC=.
①当DP与PC是对应边时,,即,
解得CQ=1,∴BQ=BC-CQ=1-1=0;
②当DP与CQ是对应边时,,即,解得CQ=,∴BQ=BC-CQ=1-.
综上所述,BQ的长度是0或时,以A,D,P为顶点的三角形与以Q,C,P为顶点的三角形相似.
15.解:①如图所示,AG,DH分别是∠BAC与∠EDF的角平分线.
②已知:如图,△ABC∽△DEF,=k,AG,DH分别是∠BAC与∠EDF的角平分线.
求证:=k.
证明:∵AG,DH分别是△ABC与△DEF的角平分线,
∴∠BAG=∠BAC,∠EDH=∠EDF.
∵△ABC∽△DEF,
∴∠BAC=∠EDF,∠B=∠E,
∴∠BAG=∠EDH,
∴△ABG∽△DEH,∴=k.
16.解:由AB=1.5
m,S△ABC=1.5
m2,得BC=2
m.
在题图1中,设甲同学加工的正方形桌面边长为x
m.
∵DE∥AB,∴Rt△CDE∽Rt△CBA,
∴,即,解得x=.
在题图2中,过点B作BH⊥AC,交AC于点H,交DE于点P.
AC==2.5
m,
BH==1.2
m.
设乙同学加工的桌面边长为y
m.
∵DE∥AC,∴△BDE∽△BAC,
∴,即,解得y=.
∵,即x>y,∴x2>y2,
∴甲同学的加工方法更好.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
