北师大版九年级上册数学第2章 一元二次方程检测卷(Word版 含答案 )
文档属性
| 名称 | 北师大版九年级上册数学第2章 一元二次方程检测卷(Word版 含答案 ) |  | |
| 格式 | zip | ||
| 文件大小 | 67.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 12:29:39 | ||
图片预览



文档简介
北师大版九年级上册数学检测卷
第二章
一元二次方程
检测卷
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.一元二次方程2x2-x+1=0根的情况是
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断
2.若x=2是方程x2-4mx+m2=0的一个根,则代数式m(m-8)-1的值是
A.-5
B.-2
C.5
D.0
3.方程(x-5)(x-6)=x-5的解是
A.x=5
B.x=5或x=6
C.x=7
D.x=5或x=7
4.若长方形的长和宽是方程4x2-12x+3=0的两个实数根,则该长方形的周长和面积分别是
A.12和3
B.6和3
C.6和
D.3和
5.关于x的方程(a-5)x2-4x-1=0有实数根,则a满足
A.a≥1
B.a>1或a≠5
C.a≥1且a≠5
D.a≠5
6.要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为
A.x(x+1)=28
B.x(x-1)=28
C.x(x+1)=28
D.x(x-1)=28
7.已知关于x的一元二次方程a(x+m)2+n=0(a≠0)的两根分别为-3,1,则方程a(x+m-2)2+n=0(a≠0)的两根分别为
A.1,5
B.-1,3
C.-3,1
D.-1,5
8.某城市2017年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2019年底增加到363公顷.设绿化面积平均每年的增长率为x,由题意,所列方程正确的是
A.300(1+x)=363
B.363(1-x)2=300
C.300(1+2x)=363
D.300(1+x)2=363
9.若x为任意实数,且M=(7-x)(3-x)(4-x2),则M的最大值为
A.10
B.84
C.100
D.121
10.对于两个不相等的实数a,b,我们规定符号Max{a,b}表示a,b中的较大值,如Max{2,4}=4,按照这个规定,方程Max{x,-x}=的解为
A.1-
B.2-
C.1+或1-
D.1+或-1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个三角形的两边长为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长是 .?
12.如果恰好只有一个实数a是关于x的方程(k2-9)x2-2(k+1)x+1=0的根,则k的值为
.?
13.小明发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:a2+b-1,例如把(3,-2)放入其中,就会得到32+(-2)-1=6.现将实数对(m,-2m)放入其中,得到实数2,则m=
.?
14.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有
.(填序号)?
①方程x2-x-2=0是倍根方程;②若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;③若p,q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;④若方程ax2+bx+c=0是倍根方程,则必有2b2=9ac.
三、(本大题共2小题,每小题8分,满分16分)
15.解下列方程:
(1)7x(3x-4)=5(3x-4);
(2)3x2+5(2x+1)=0.
16.一元二次方程a(x2+1)+b(x+2)+c=0化为一般式后为6x2+10x-1=0,求以a,b为两条对角线长的菱形的面积.
四、(本大题共2小题,每小题8分,满分16分)
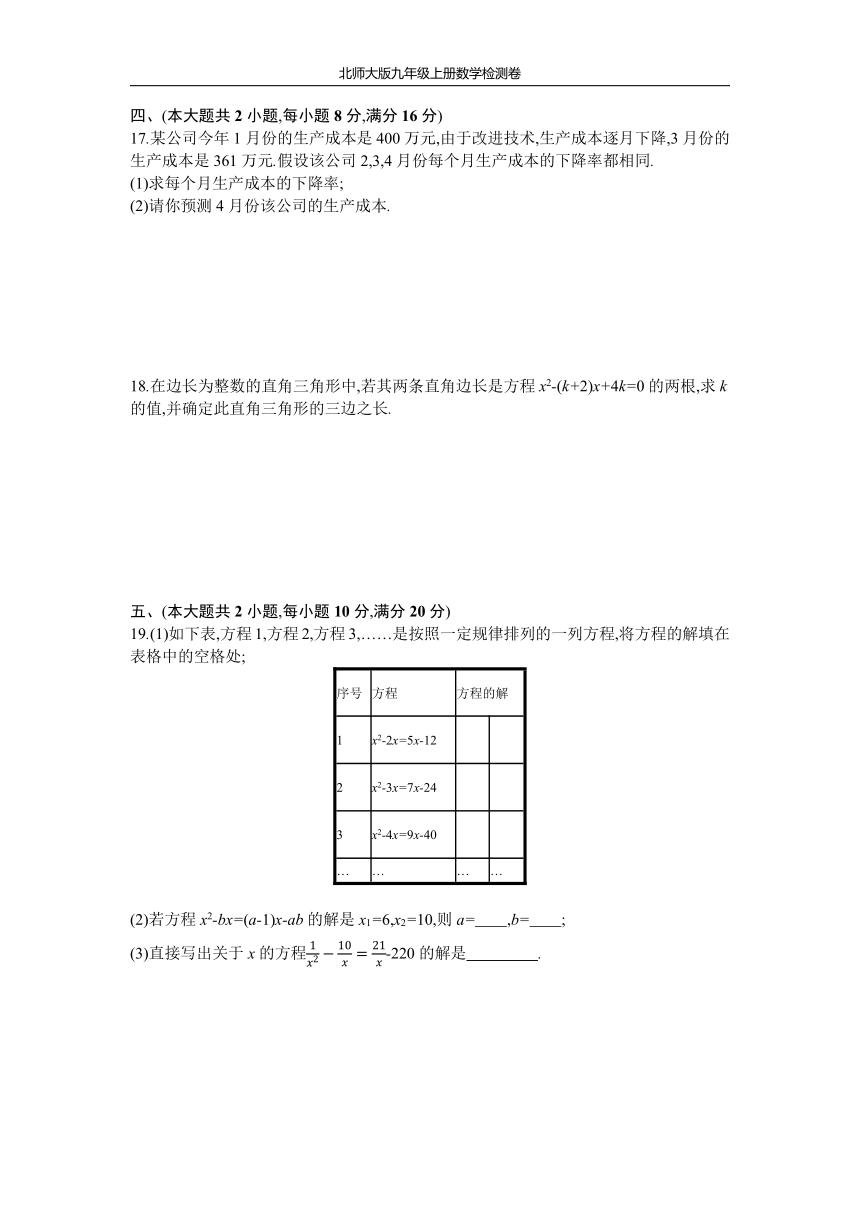
17.某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2,3,4月份每个月生产成本的下降率都相同.
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本.
18.在边长为整数的直角三角形中,若其两条直角边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定此直角三角形的三边之长.
五、(本大题共2小题,每小题10分,满分20分)
19.(1)如下表,方程1,方程2,方程3,……是按照一定规律排列的一列方程,将方程的解填在表格中的空格处;
序号
方程
方程的解
1
x2-2x=5x-12
2
x2-3x=7x-24
3
x2-4x=9x-40
…
…
…
…
(2)若方程x2-bx=(a-1)x-ab的解是x1=6,x2=10,则a= ,b= ;?
(3)直接写出关于x的方程-220的解是
.?
20.已知k为非负实数,关于x的方程x2-(k+1)x+k=0和kx2-(k+2)x+k=0.
(1)求证:前一个方程必有两个非负实数根.
(2)当k取何值时,上述两个方程有一个相同的实数根?
六、(本题满分12分)
21.某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天的产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
七、(本题满分12分)
22.某旅行社推出“跟团游”和“定制游”两种旅行方式供客户选择.已知6月份该旅行社“跟团游”的销售额为60万元,“定制游”的销售额为20万元,“跟团游”平均每单的费用比“定制游”平均每单的费用少0.1万元,“跟团游”的订单数是“定制游”订单数的4倍,订单按一人一单计算.
(1)求“定制游”的单数为多少?
(2)由于暑期是旅游旺季,消费水平整体升高,该旅行社预计7月份“跟团游”和“定制游”的订单数分别比上月对应订单数多3a%和a%,“跟团游”和“定制游”平均每单的费用分别比上月对应每单多a%和2a%,这样预计7月份该旅行社总销售额比上个月总销售额的7a%还多40万元,且a>50,求a的值.
八、(本题满分14分)
23.实验与探究:
三角点阵中前n行的点数计算
下图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,……,第n行有n个点.
容易发现,10是三角点阵中前4行的点数和.你能发现300是前多少行的点数和吗?如果用实验的方法,由上而下地逐行相加其点数,虽然你能发现1+2+3+…+23+24=300,得知300是前24行的点数和,但是这样寻找答案需要花费较多时间,能否更简捷地得出结果呢?
我们先探究三角点阵中前n行的点数和与n的数量关系.
前n行的点数和是1+2+3+…+(n-2)+(n-1)+n.可以发现,
2×[1+2+3+…+(n-2)+(n-1)+n]=[1+2+3+…+(n-2)+(n-1)+n]+[n+(n-1)+(n-2)+…+3+2+1].
把两个中括号中的第一项相加,第二项相加,……,第n项相加,上式等号的后边变形为n个n+1相加,整个式子等于n(n+1),于是得到1+2+3+…+(n-2)+(n-1)+n=n(n+1).
这就是说,三角点阵中前n行的点数和是n(n+1).
下面用一元二次方程解决上述问题:设三角点阵中前n行的点数和为300,则有n(n+1)=300,
整理这个方程,得n2+n-600=0.
解方程得n1=24,n2=-25.
根据问题中未知数的意义确定n=24,即三角点阵中前24行的和是300.
请你根据上述材料回答下列问题:
(1)三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
(2)如果把图中的三角点阵中各行的点数依次换为2,4,6,…,2n,你能探究出前n行的点数和满足什么规律吗?这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
A
D
C
A
B
B
D
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 13
12. ±3或-5
13. 3或-1
14. ②③④
三、(本大题共2小题,每小题8分,满分16分)
15.
(1)解:x1=,x2=.
(2)解:x1=,x2=-.
16.解:方程经整理,得ax2+bx+a+2b+c=0.
∵6x2+10x-1=0,∴a=6,b=10,
∴S菱形=×6×10=30.
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)设每个月生产成本的下降率为x,
根据题意得400(1-x)2=361,
解得x1=0.05=5%,x2=1.95(不合题意,舍去).
答:每个月生产成本的下降率为5%.
(2)361×(1-5%)=342.95(万元).
答:预测4月份该公司的生产成本为342.95万元.
18.解:设两条直角边长分别为a,b(a∵a,b为整数,∴k>0,k也是整数,且方程x2-(k+2)x+4k=0的判别式为平方数,
设Δ=(k+2)2-16k=n2,∴(k-6)2-32=n2,
根据(k-6)2-32是一个平方数,k>0,k是整数,
∴k=12或15,
当k=12时,解得a=6,b=8,∴c=10.
当k=15时,解得a=5,b=12,∴c=13,
∴当k=12时,三角形三边的长为6,8,10;
当k=15时,三角形三边的长为5,12,13.
五、(本大题共2小题,每小题10分,满分20分)
19.(1)
序号
方程
方程的解
1
x2-2x=5x-12
x1=3
x2=4
2
x2-3x=7x-24
x1=4
x2=6
3
x2-4x=9x-40
x1=5
x2=8
…
…
…
…
(2) 12 5
(3) x1=,x2=
解:(3)提示:设t=,则原方程化为t2-10t=21t-220,
它的解为t1=11,t2=20,所以x1=,x2=.
经检验x1=,x2=是原方程的解.
20.解:(1)Δ=[-(k+1)]2-4k=k2-2k+1=(k-1)2≥0,
即关于x的方程x2-(k+1)x+k=0一定有两个实数根.
设方程的两根为x1,x2,则x1+x2=k+1,x1x2=k.
∵k为非负实数,∴x1+x2=k+1>0,x1x2=k≥0.
由x1x2=k≥0得出方程有同号两个根或有一个根为0;
由x1+x2=k+1>0,x1x2=k≥0得出方程有两个正实数根或有一个根为0,
∴方程x2-(k+1)x+k=0必有两个非负实数根.
(2)对于方程x2-(k+1)x+k=0,Δ=(k-1)2≥0,
方程的根为,即方程的根为k和1.
当相同的根是k时,把x=k代入方程kx2-(k+2)x+k=0,得k3-(k+2)k+k=0,解得k=0或k=或k=,
∵k为非负实数,∴k=0或;
当相同的根是1时,把x=1代入方程kx2-(k+2)x+k=0,得k-(k+2)+k=0,解得k=2.
∴当k=2或0或时,上述两个方程有一个相同的实数根.
六、(本题满分12分)
21.解:(1)依题意得y=[6+2(x-1)]×[95-5(x-1)],
整理,得y=-10x2+180x+400.
(2)由-10x2+180x+400=1120化简,得x2-18x+72=0,
配方,得(x-9)2=9,解得x1=6,x2=12(不合题意,舍去).
答:该产品为第6档次的产品.
七、(本题满分12分)
22.解:(1)设“定制游”的单数为x,
根据题意,得4x×=60,解得x=50.
经检验,x=50是原方程的解,也符合问题的实际意义.
答:“定制游”的单数为50.
(2)由题意得60(1+3a%)(1+a%)+20(1+a%)(1+2a%)=(20+60)×7a%+40,
化简得11a2-1300a+20000=0,解得a1=100,a2=,
∵a>50,∴a=100.
八、(本题满分14分)
23.解:(1)三角点阵中前n行的点数和不能是600.
由题意得n(n+1)=600,
整理这个方程,得n2+n-1200=0,此方程无正整数解,
∴三角点阵中前n行的点数和不能是600.
(2)∵1+2+3+…+(n-2)+(n-1)+n=n(n+1),
∴2+4+6+…+2n=2(1+2+3…+n)=2×n(n+1)=n(n+1).
由题意得n(n+1)=600,解方程得n1=24,n2=-25(舍去).
根据题意确定n=24,即三角点阵中前24行的和是600.
第二章
一元二次方程
检测卷
(120分钟 150分)
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
1.一元二次方程2x2-x+1=0根的情况是
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断
2.若x=2是方程x2-4mx+m2=0的一个根,则代数式m(m-8)-1的值是
A.-5
B.-2
C.5
D.0
3.方程(x-5)(x-6)=x-5的解是
A.x=5
B.x=5或x=6
C.x=7
D.x=5或x=7
4.若长方形的长和宽是方程4x2-12x+3=0的两个实数根,则该长方形的周长和面积分别是
A.12和3
B.6和3
C.6和
D.3和
5.关于x的方程(a-5)x2-4x-1=0有实数根,则a满足
A.a≥1
B.a>1或a≠5
C.a≥1且a≠5
D.a≠5
6.要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为
A.x(x+1)=28
B.x(x-1)=28
C.x(x+1)=28
D.x(x-1)=28
7.已知关于x的一元二次方程a(x+m)2+n=0(a≠0)的两根分别为-3,1,则方程a(x+m-2)2+n=0(a≠0)的两根分别为
A.1,5
B.-1,3
C.-3,1
D.-1,5
8.某城市2017年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2019年底增加到363公顷.设绿化面积平均每年的增长率为x,由题意,所列方程正确的是
A.300(1+x)=363
B.363(1-x)2=300
C.300(1+2x)=363
D.300(1+x)2=363
9.若x为任意实数,且M=(7-x)(3-x)(4-x2),则M的最大值为
A.10
B.84
C.100
D.121
10.对于两个不相等的实数a,b,我们规定符号Max{a,b}表示a,b中的较大值,如Max{2,4}=4,按照这个规定,方程Max{x,-x}=的解为
A.1-
B.2-
C.1+或1-
D.1+或-1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个三角形的两边长为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长是 .?
12.如果恰好只有一个实数a是关于x的方程(k2-9)x2-2(k+1)x+1=0的根,则k的值为
.?
13.小明发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:a2+b-1,例如把(3,-2)放入其中,就会得到32+(-2)-1=6.现将实数对(m,-2m)放入其中,得到实数2,则m=
.?
14.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有
.(填序号)?
①方程x2-x-2=0是倍根方程;②若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;③若p,q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;④若方程ax2+bx+c=0是倍根方程,则必有2b2=9ac.
三、(本大题共2小题,每小题8分,满分16分)
15.解下列方程:
(1)7x(3x-4)=5(3x-4);
(2)3x2+5(2x+1)=0.
16.一元二次方程a(x2+1)+b(x+2)+c=0化为一般式后为6x2+10x-1=0,求以a,b为两条对角线长的菱形的面积.
四、(本大题共2小题,每小题8分,满分16分)
17.某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2,3,4月份每个月生产成本的下降率都相同.
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本.
18.在边长为整数的直角三角形中,若其两条直角边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定此直角三角形的三边之长.
五、(本大题共2小题,每小题10分,满分20分)
19.(1)如下表,方程1,方程2,方程3,……是按照一定规律排列的一列方程,将方程的解填在表格中的空格处;
序号
方程
方程的解
1
x2-2x=5x-12
2
x2-3x=7x-24
3
x2-4x=9x-40
…
…
…
…
(2)若方程x2-bx=(a-1)x-ab的解是x1=6,x2=10,则a= ,b= ;?
(3)直接写出关于x的方程-220的解是
.?
20.已知k为非负实数,关于x的方程x2-(k+1)x+k=0和kx2-(k+2)x+k=0.
(1)求证:前一个方程必有两个非负实数根.
(2)当k取何值时,上述两个方程有一个相同的实数根?
六、(本题满分12分)
21.某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天的产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
七、(本题满分12分)
22.某旅行社推出“跟团游”和“定制游”两种旅行方式供客户选择.已知6月份该旅行社“跟团游”的销售额为60万元,“定制游”的销售额为20万元,“跟团游”平均每单的费用比“定制游”平均每单的费用少0.1万元,“跟团游”的订单数是“定制游”订单数的4倍,订单按一人一单计算.
(1)求“定制游”的单数为多少?
(2)由于暑期是旅游旺季,消费水平整体升高,该旅行社预计7月份“跟团游”和“定制游”的订单数分别比上月对应订单数多3a%和a%,“跟团游”和“定制游”平均每单的费用分别比上月对应每单多a%和2a%,这样预计7月份该旅行社总销售额比上个月总销售额的7a%还多40万元,且a>50,求a的值.
八、(本题满分14分)
23.实验与探究:
三角点阵中前n行的点数计算
下图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,……,第n行有n个点.
容易发现,10是三角点阵中前4行的点数和.你能发现300是前多少行的点数和吗?如果用实验的方法,由上而下地逐行相加其点数,虽然你能发现1+2+3+…+23+24=300,得知300是前24行的点数和,但是这样寻找答案需要花费较多时间,能否更简捷地得出结果呢?
我们先探究三角点阵中前n行的点数和与n的数量关系.
前n行的点数和是1+2+3+…+(n-2)+(n-1)+n.可以发现,
2×[1+2+3+…+(n-2)+(n-1)+n]=[1+2+3+…+(n-2)+(n-1)+n]+[n+(n-1)+(n-2)+…+3+2+1].
把两个中括号中的第一项相加,第二项相加,……,第n项相加,上式等号的后边变形为n个n+1相加,整个式子等于n(n+1),于是得到1+2+3+…+(n-2)+(n-1)+n=n(n+1).
这就是说,三角点阵中前n行的点数和是n(n+1).
下面用一元二次方程解决上述问题:设三角点阵中前n行的点数和为300,则有n(n+1)=300,
整理这个方程,得n2+n-600=0.
解方程得n1=24,n2=-25.
根据问题中未知数的意义确定n=24,即三角点阵中前24行的和是300.
请你根据上述材料回答下列问题:
(1)三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
(2)如果把图中的三角点阵中各行的点数依次换为2,4,6,…,2n,你能探究出前n行的点数和满足什么规律吗?这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
C
A
D
C
A
B
B
D
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 13
12. ±3或-5
13. 3或-1
14. ②③④
三、(本大题共2小题,每小题8分,满分16分)
15.
(1)解:x1=,x2=.
(2)解:x1=,x2=-.
16.解:方程经整理,得ax2+bx+a+2b+c=0.
∵6x2+10x-1=0,∴a=6,b=10,
∴S菱形=×6×10=30.
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)设每个月生产成本的下降率为x,
根据题意得400(1-x)2=361,
解得x1=0.05=5%,x2=1.95(不合题意,舍去).
答:每个月生产成本的下降率为5%.
(2)361×(1-5%)=342.95(万元).
答:预测4月份该公司的生产成本为342.95万元.
18.解:设两条直角边长分别为a,b(a
设Δ=(k+2)2-16k=n2,∴(k-6)2-32=n2,
根据(k-6)2-32是一个平方数,k>0,k是整数,
∴k=12或15,
当k=12时,解得a=6,b=8,∴c=10.
当k=15时,解得a=5,b=12,∴c=13,
∴当k=12时,三角形三边的长为6,8,10;
当k=15时,三角形三边的长为5,12,13.
五、(本大题共2小题,每小题10分,满分20分)
19.(1)
序号
方程
方程的解
1
x2-2x=5x-12
x1=3
x2=4
2
x2-3x=7x-24
x1=4
x2=6
3
x2-4x=9x-40
x1=5
x2=8
…
…
…
…
(2) 12 5
(3) x1=,x2=
解:(3)提示:设t=,则原方程化为t2-10t=21t-220,
它的解为t1=11,t2=20,所以x1=,x2=.
经检验x1=,x2=是原方程的解.
20.解:(1)Δ=[-(k+1)]2-4k=k2-2k+1=(k-1)2≥0,
即关于x的方程x2-(k+1)x+k=0一定有两个实数根.
设方程的两根为x1,x2,则x1+x2=k+1,x1x2=k.
∵k为非负实数,∴x1+x2=k+1>0,x1x2=k≥0.
由x1x2=k≥0得出方程有同号两个根或有一个根为0;
由x1+x2=k+1>0,x1x2=k≥0得出方程有两个正实数根或有一个根为0,
∴方程x2-(k+1)x+k=0必有两个非负实数根.
(2)对于方程x2-(k+1)x+k=0,Δ=(k-1)2≥0,
方程的根为,即方程的根为k和1.
当相同的根是k时,把x=k代入方程kx2-(k+2)x+k=0,得k3-(k+2)k+k=0,解得k=0或k=或k=,
∵k为非负实数,∴k=0或;
当相同的根是1时,把x=1代入方程kx2-(k+2)x+k=0,得k-(k+2)+k=0,解得k=2.
∴当k=2或0或时,上述两个方程有一个相同的实数根.
六、(本题满分12分)
21.解:(1)依题意得y=[6+2(x-1)]×[95-5(x-1)],
整理,得y=-10x2+180x+400.
(2)由-10x2+180x+400=1120化简,得x2-18x+72=0,
配方,得(x-9)2=9,解得x1=6,x2=12(不合题意,舍去).
答:该产品为第6档次的产品.
七、(本题满分12分)
22.解:(1)设“定制游”的单数为x,
根据题意,得4x×=60,解得x=50.
经检验,x=50是原方程的解,也符合问题的实际意义.
答:“定制游”的单数为50.
(2)由题意得60(1+3a%)(1+a%)+20(1+a%)(1+2a%)=(20+60)×7a%+40,
化简得11a2-1300a+20000=0,解得a1=100,a2=,
∵a>50,∴a=100.
八、(本题满分14分)
23.解:(1)三角点阵中前n行的点数和不能是600.
由题意得n(n+1)=600,
整理这个方程,得n2+n-1200=0,此方程无正整数解,
∴三角点阵中前n行的点数和不能是600.
(2)∵1+2+3+…+(n-2)+(n-1)+n=n(n+1),
∴2+4+6+…+2n=2(1+2+3…+n)=2×n(n+1)=n(n+1).
由题意得n(n+1)=600,解方程得n1=24,n2=-25(舍去).
根据题意确定n=24,即三角点阵中前24行的和是600.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
