湘教版七年级数学上册第4章 图形的认识达标测试卷(Word版 含答案)
文档属性
| 名称 | 湘教版七年级数学上册第4章 图形的认识达标测试卷(Word版 含答案) | 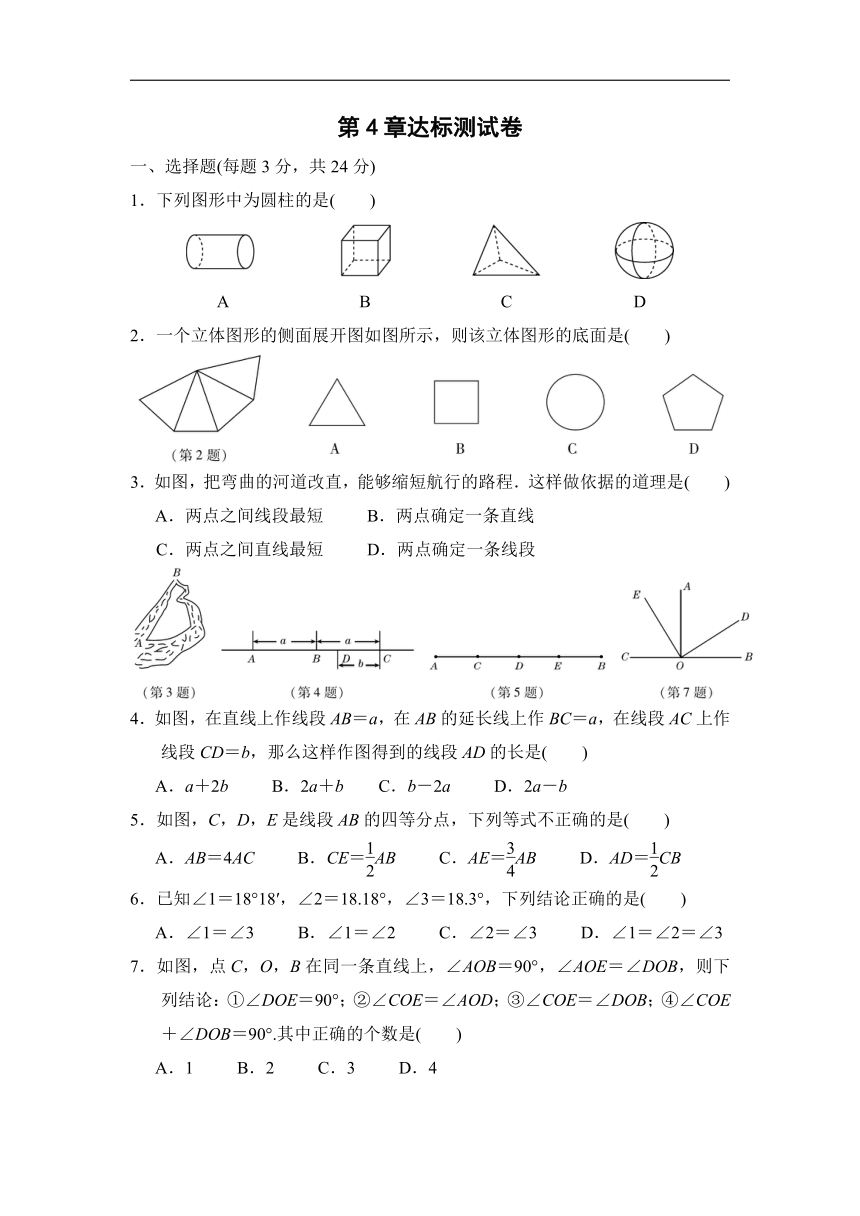 | |
| 格式 | doc | ||
| 文件大小 | 230.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 15:24:02 | ||
图片预览



文档简介
第4章达标测试卷
一、选择题(每题3分,共24分)
1.下列图形中为圆柱的是( )
A B C D
2.一个立体图形的侧面展开图如图所示,则该立体图形的底面是( )
3.如图,把弯曲的河道改直,能够缩短航行的路程.这样做依据的道理是( )
A.两点之间线段最短 B.两点确定一条直线
C.两点之间直线最短 D.两点确定一条线段
4.如图,在直线上作线段AB=a,在AB的延长线上作BC=a,在线段AC上作线段CD=b,那么这样作图得到的线段AD的长是( )
A.a+2b B.2a+b C.b-2a D.2a-b
5.如图,C,D,E是线段AB的四等分点,下列等式不正确的是( )
A.AB=4AC B.CE=AB C.AE=AB D.AD=CB
6.已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3 B.∠1=∠2 C.∠2=∠3 D.∠1=∠2=∠3
7.如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠DOE=90°;②∠COE=∠AOD;③∠COE=∠DOB;④∠COE+∠DOB=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
8.9:30时,钟面上的时针与分针间的夹角是( )
A.75° B.90°
C.105° D.120°
二、填空题(每题4分,共32分)
9.如图,点A,B,C在直线l上,则图中共有________条线段.
10.已知∠α=72°36′,则∠α的余角是________ .
11.线段AB=2 cm,延长AB至点C,使BC=2AB,则AC=________ cm.
12.直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的是________(填序号).
13.如图,已知∠DOB+∠BOC=90°,∠AOC+∠BOC=90°,则∠DOB=∠AOC的理由是______________.
14.如图是一个正方体纸盒的表面展开图,正方体纸盒的各面标有数1,2,3,-3,A,B,相对面上的两个数互为相反数,则A=________;B=________.
15.如图,线段AC=6 cm,线段BC=15 cm,点M是AC的中点,在CB上取一点N,使得CN∶NB=1∶2,则MN的长为________.
16.如图,OM是∠AOB的平分线,OP是∠MOB内的一条射线.已知∠AOP比∠BOP大30°,则∠MOP的度数为________.
三、解答题(17~19题每题8分,其余每题10分,共44分)
17.计算:
(1)180°-91°32′24″;
(2)34°26′×3+35°42′;
(3) 51°37′11″-30°30′30″÷5;
(4) 13°53′×3-32°5′31″.
18.如图,已知线段a,b(a>b),画一条线段,使它等于2a-2b.
(第18题)
19.如图,AD∶DB =1∶2,E是BC的中点,BE∶AC =1∶5.若BE=2 cm,求线段DE的长.
(第19题)
20.如图,已知O是直线AB上一点,∠BOE=∠FOD=90°,OB平分∠COD.
(1)图中与∠DOE互余的角是________________;
(2)图中与∠DOE互补的角是____________;
(3)若∠EOD∶∠EOF=3∶2,求∠AOC的度数.
(第20题)
21.新规定:点C为线段AB上一点,当CA=3CB或CB=3CA时,我们就规定C为线段AB的“三倍距点”.如图,在数轴上,点A表示的数为-3,点B表示的数为5.
(第21题)
(1)点C所表示的数为____________;
(2)若动点P从点B出发,沿射线BA方向以每秒2个单位长度的速度运动,设运动时间为t秒.
①当点P与点A重合时,t=________;
②求AP的长度(用含t的代数式表示);
③当点A为线段BP的“三倍距点”时,求t的值.
答案
一、1.A 2.B 3.A 4.D 5.D 6.A
7.C 点拨:因为∠AOB=90°,所以∠AOD+∠DOB=90°.
因为∠AOE=∠DOB,所以∠AOE+∠AOD=90°, 即∠DOE=90°.因为点C,O,B在同一条直线上,所以∠COE+∠DOB=90°,所以∠COE=∠AOD.故①②④正确.
8.C 点拨:钟面上的时针与分针间的夹角为3×30°+30°×=105°.
二、9.3 10.17°24′ 11.6 12.③ 13.同角的余角相等 14.-2;-1
15.8 cm 点拨:因为M是AC的中点,所以MC=AC=×6=3(cm).
又因为CN∶NB=1∶2,
所以CN=BC=×15=5 (cm).
所以MN=MC+NC=3+5=8(cm).
16.15° 点拨:因为OM是∠AOB的平分线,所以∠AOM=∠BOM.
因为∠AOP比∠BOP大30°, 即∠AOM+∠MOP-∠BOP=30°, 所以∠AOM+∠MOP-(∠BOM-∠MOP)=30°,
所以2∠MOP=30°,所以∠MOP=15°.
三、17.解:(1)原式=179°59′60″-91°32′24″ =88°27′36″.
(2)原式=102°78′+35°42′=139°.
(3)原式=51°37′11″-6°6′6″=45°31′5″.
(4)原式=39°159′-32°5′31″=41°38′60″-32°5′31″=9°33′29″.
18.解:如图,作法:①作射线AF;
②在射线AF上顺次截取AB=BC=a;
③在线段AC上顺次截取AD=DE=b,则线段EC即为所求作的线段.
(第18题)
19.解:由于BE∶AC =1∶5,BE=2 cm,所以AC=5BE=10 cm.
因为E是BC的中点,
所以BE=EC=2 cm,BC=2BE=2×2=4(cm),
所以AB=AC-BC=10-4=6(cm).
又因为AD∶DB =1∶2,
所以AB=AD+DB=AD+2AD=3AD=6 cm,所以AD=2 cm,
所以DE=AC-AD-EC=10-2-2=6(cm).
20.解:(1)∠EOF,∠BOD,∠BOC
(2)∠BOF,∠COE
(3)因为∠EOD∶∠EOF=3∶2,
所以可设∠EOD=3x,则∠EOF=2x.
因为∠FOD=90°,
所以3x+2x=90°,解得x=18°,所以∠EOF=36°.
因为∠BOE=∠FOD=90°,
所以∠DOE+∠EOF=90°,∠DOE+∠DOB=90°,
所以∠DOB=∠EOF=36°.
因为OB平分∠COD,所以∠COB=∠DOB=36°.
因为∠AOC+∠COB=180°,
所以∠AOC=180°-∠COB=144°.
21.解:(1)-1或3 点拨:设点C表示的数为c,
当CA=3CB时,c-(-3)=3(5-c),解得c=3,
当CB=3CA时,5-c=3[c-(-3)],解得c=-1.
(2)①4
②当点P在点A右侧时,AP=8-2t.
当点P在点A左侧时,AP=2t-8.
③设点P表示的数为p,
当PA=3AB时,-3-p=3×[5-(-3)],解得p=-27,
所以BP=5-(-27)=32,所以t==16;
当AB=3PA时,5-(-3)=3(-3-p),解得p=-,
所以BP=5-=,所以t=÷2=.
综上所述,t的值为或16.
一、选择题(每题3分,共24分)
1.下列图形中为圆柱的是( )
A B C D
2.一个立体图形的侧面展开图如图所示,则该立体图形的底面是( )
3.如图,把弯曲的河道改直,能够缩短航行的路程.这样做依据的道理是( )
A.两点之间线段最短 B.两点确定一条直线
C.两点之间直线最短 D.两点确定一条线段
4.如图,在直线上作线段AB=a,在AB的延长线上作BC=a,在线段AC上作线段CD=b,那么这样作图得到的线段AD的长是( )
A.a+2b B.2a+b C.b-2a D.2a-b
5.如图,C,D,E是线段AB的四等分点,下列等式不正确的是( )
A.AB=4AC B.CE=AB C.AE=AB D.AD=CB
6.已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3 B.∠1=∠2 C.∠2=∠3 D.∠1=∠2=∠3
7.如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠DOE=90°;②∠COE=∠AOD;③∠COE=∠DOB;④∠COE+∠DOB=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
8.9:30时,钟面上的时针与分针间的夹角是( )
A.75° B.90°
C.105° D.120°
二、填空题(每题4分,共32分)
9.如图,点A,B,C在直线l上,则图中共有________条线段.
10.已知∠α=72°36′,则∠α的余角是________ .
11.线段AB=2 cm,延长AB至点C,使BC=2AB,则AC=________ cm.
12.直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的是________(填序号).
13.如图,已知∠DOB+∠BOC=90°,∠AOC+∠BOC=90°,则∠DOB=∠AOC的理由是______________.
14.如图是一个正方体纸盒的表面展开图,正方体纸盒的各面标有数1,2,3,-3,A,B,相对面上的两个数互为相反数,则A=________;B=________.
15.如图,线段AC=6 cm,线段BC=15 cm,点M是AC的中点,在CB上取一点N,使得CN∶NB=1∶2,则MN的长为________.
16.如图,OM是∠AOB的平分线,OP是∠MOB内的一条射线.已知∠AOP比∠BOP大30°,则∠MOP的度数为________.
三、解答题(17~19题每题8分,其余每题10分,共44分)
17.计算:
(1)180°-91°32′24″;
(2)34°26′×3+35°42′;
(3) 51°37′11″-30°30′30″÷5;
(4) 13°53′×3-32°5′31″.
18.如图,已知线段a,b(a>b),画一条线段,使它等于2a-2b.
(第18题)
19.如图,AD∶DB =1∶2,E是BC的中点,BE∶AC =1∶5.若BE=2 cm,求线段DE的长.
(第19题)
20.如图,已知O是直线AB上一点,∠BOE=∠FOD=90°,OB平分∠COD.
(1)图中与∠DOE互余的角是________________;
(2)图中与∠DOE互补的角是____________;
(3)若∠EOD∶∠EOF=3∶2,求∠AOC的度数.
(第20题)
21.新规定:点C为线段AB上一点,当CA=3CB或CB=3CA时,我们就规定C为线段AB的“三倍距点”.如图,在数轴上,点A表示的数为-3,点B表示的数为5.
(第21题)
(1)点C所表示的数为____________;
(2)若动点P从点B出发,沿射线BA方向以每秒2个单位长度的速度运动,设运动时间为t秒.
①当点P与点A重合时,t=________;
②求AP的长度(用含t的代数式表示);
③当点A为线段BP的“三倍距点”时,求t的值.
答案
一、1.A 2.B 3.A 4.D 5.D 6.A
7.C 点拨:因为∠AOB=90°,所以∠AOD+∠DOB=90°.
因为∠AOE=∠DOB,所以∠AOE+∠AOD=90°, 即∠DOE=90°.因为点C,O,B在同一条直线上,所以∠COE+∠DOB=90°,所以∠COE=∠AOD.故①②④正确.
8.C 点拨:钟面上的时针与分针间的夹角为3×30°+30°×=105°.
二、9.3 10.17°24′ 11.6 12.③ 13.同角的余角相等 14.-2;-1
15.8 cm 点拨:因为M是AC的中点,所以MC=AC=×6=3(cm).
又因为CN∶NB=1∶2,
所以CN=BC=×15=5 (cm).
所以MN=MC+NC=3+5=8(cm).
16.15° 点拨:因为OM是∠AOB的平分线,所以∠AOM=∠BOM.
因为∠AOP比∠BOP大30°, 即∠AOM+∠MOP-∠BOP=30°, 所以∠AOM+∠MOP-(∠BOM-∠MOP)=30°,
所以2∠MOP=30°,所以∠MOP=15°.
三、17.解:(1)原式=179°59′60″-91°32′24″ =88°27′36″.
(2)原式=102°78′+35°42′=139°.
(3)原式=51°37′11″-6°6′6″=45°31′5″.
(4)原式=39°159′-32°5′31″=41°38′60″-32°5′31″=9°33′29″.
18.解:如图,作法:①作射线AF;
②在射线AF上顺次截取AB=BC=a;
③在线段AC上顺次截取AD=DE=b,则线段EC即为所求作的线段.
(第18题)
19.解:由于BE∶AC =1∶5,BE=2 cm,所以AC=5BE=10 cm.
因为E是BC的中点,
所以BE=EC=2 cm,BC=2BE=2×2=4(cm),
所以AB=AC-BC=10-4=6(cm).
又因为AD∶DB =1∶2,
所以AB=AD+DB=AD+2AD=3AD=6 cm,所以AD=2 cm,
所以DE=AC-AD-EC=10-2-2=6(cm).
20.解:(1)∠EOF,∠BOD,∠BOC
(2)∠BOF,∠COE
(3)因为∠EOD∶∠EOF=3∶2,
所以可设∠EOD=3x,则∠EOF=2x.
因为∠FOD=90°,
所以3x+2x=90°,解得x=18°,所以∠EOF=36°.
因为∠BOE=∠FOD=90°,
所以∠DOE+∠EOF=90°,∠DOE+∠DOB=90°,
所以∠DOB=∠EOF=36°.
因为OB平分∠COD,所以∠COB=∠DOB=36°.
因为∠AOC+∠COB=180°,
所以∠AOC=180°-∠COB=144°.
21.解:(1)-1或3 点拨:设点C表示的数为c,
当CA=3CB时,c-(-3)=3(5-c),解得c=3,
当CB=3CA时,5-c=3[c-(-3)],解得c=-1.
(2)①4
②当点P在点A右侧时,AP=8-2t.
当点P在点A左侧时,AP=2t-8.
③设点P表示的数为p,
当PA=3AB时,-3-p=3×[5-(-3)],解得p=-27,
所以BP=5-(-27)=32,所以t==16;
当AB=3PA时,5-(-3)=3(-3-p),解得p=-,
所以BP=5-=,所以t=÷2=.
综上所述,t的值为或16.
同课章节目录
