第一章 特殊平行四边形 回顾与思考课件(共30张PPT)
文档属性
| 名称 | 第一章 特殊平行四边形 回顾与思考课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 14:11:28 | ||
图片预览


文档简介
第一章
特殊平行四边形
专题复习
2020年秋北师大版九年级上册
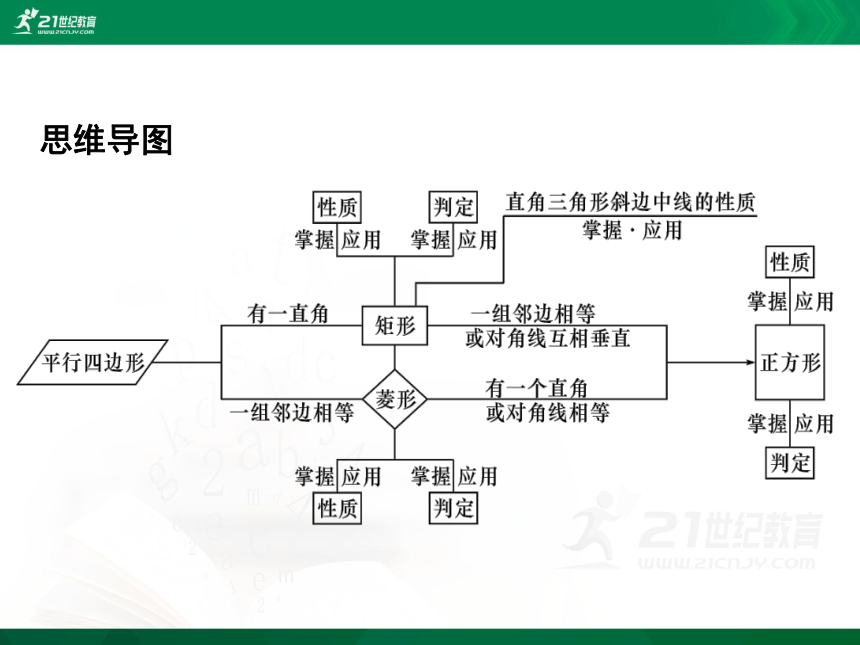
思维导图
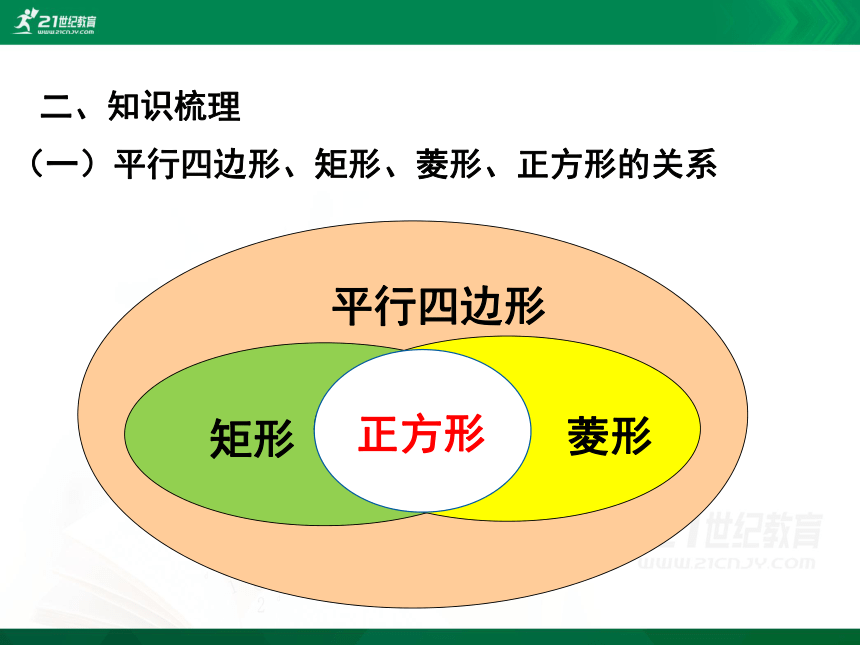
(一)平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
二、知识梳理
{5940675A-B579-460E-94D1-54222C63F5DA}
菱形
矩形
正方形
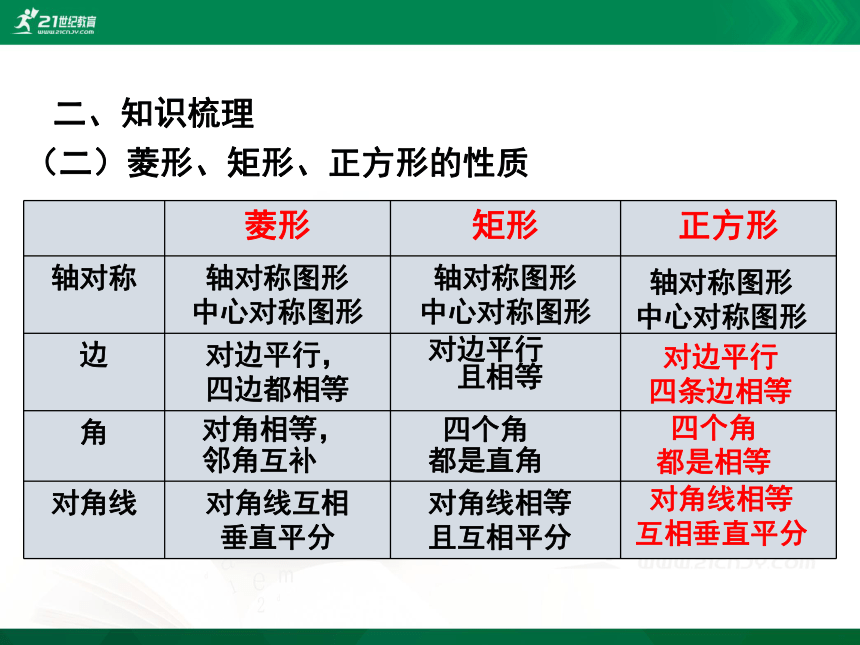
轴对称
轴对称图形
中心对称图形
轴对称图形
中心对称图形
边
对边平行,
四边都相等
对边平行
且相等
角
对角相等,
邻角互补
四个角
都是直角
对角线
对角线互相
垂直平分
对角线相等
且互相平分
轴对称图形
中心对称图形
对边平行
四条边相等
四个角
都是相等
对角线相等
互相垂直平分
(二)菱形、矩形、正方形的性质
二、知识梳理
四边形
条件
矩形
菱形
正方形
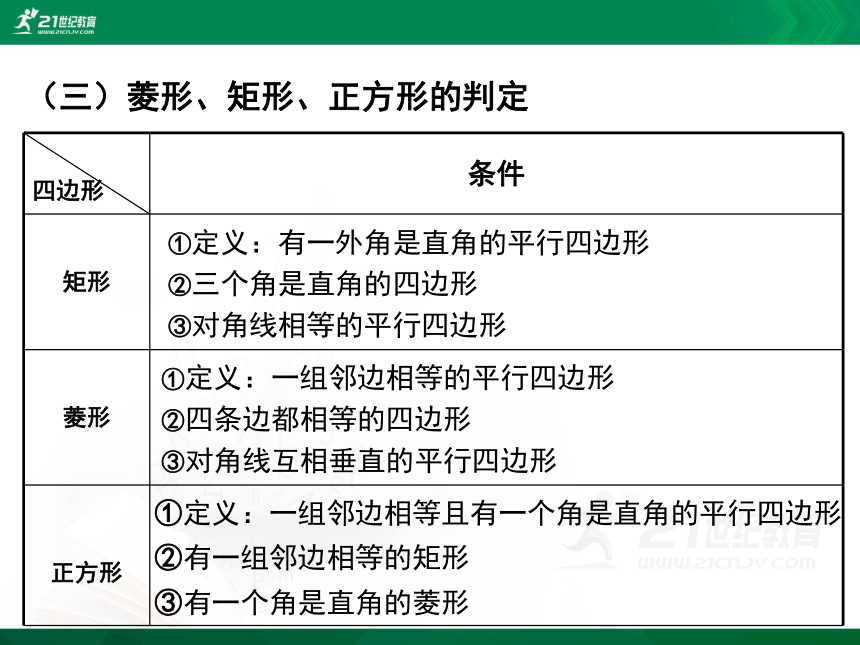
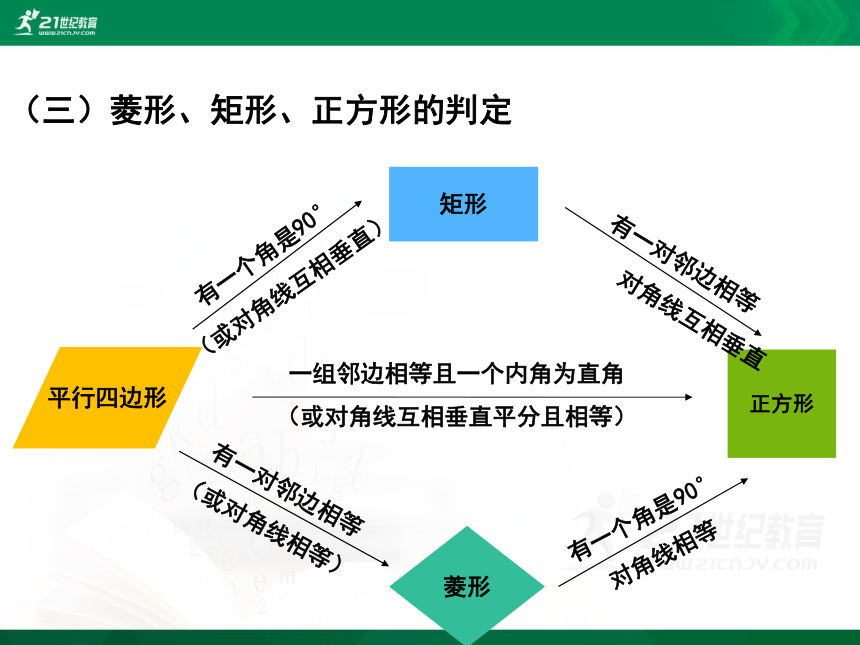
(三)菱形、矩形、正方形的判定
①定义:有一外角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形
有一个角是90°
(或对角线互相垂直)
有一对邻边相等
(或对角线相等)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)
有一个角是90°
对角线相等
有一对邻边相等
对角线互相垂直
(三)菱形、矩形、正方形的判定
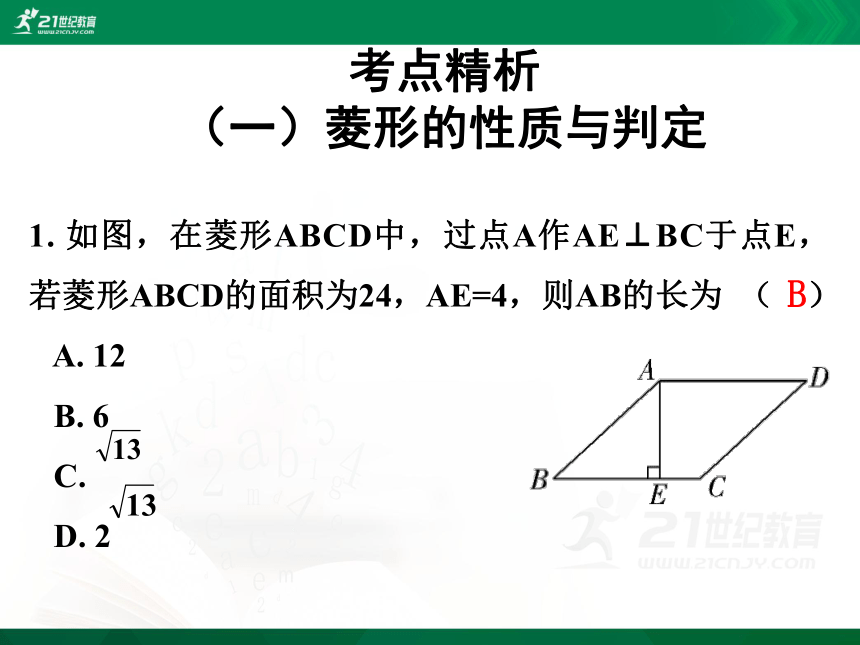
1. 如图,在菱形ABCD中,过点A作AE⊥BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为 ( )
A. 12
B. 6
C.
D. 2
B
考点精析
(一)菱形的性质与判定
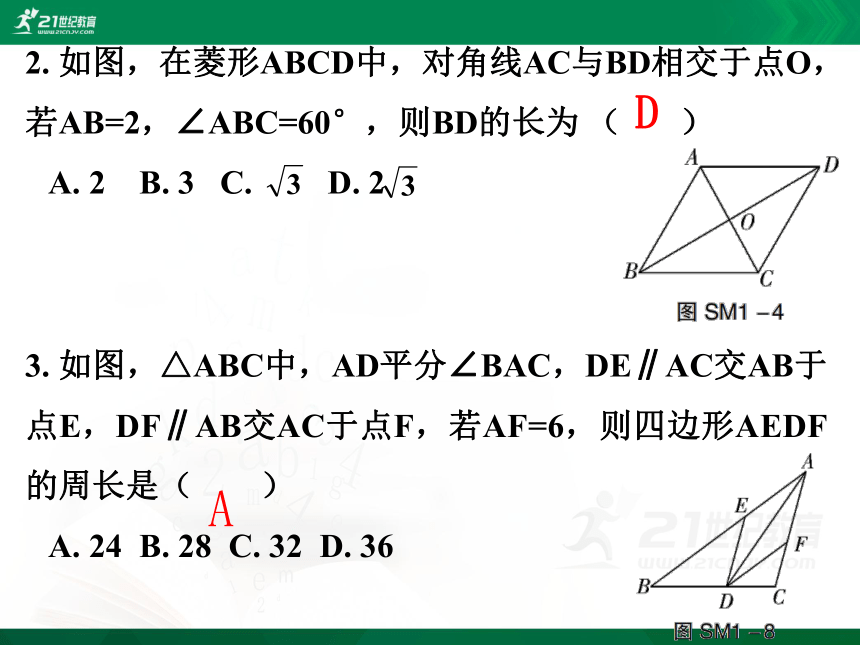
2. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为 ( )
A. 2 B. 3 C. D. 2
D
3. 如图,△ABC中,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,若AF=6,则四边形AEDF的周长是( )
A. 24 B. 28 C. 32 D. 36
A
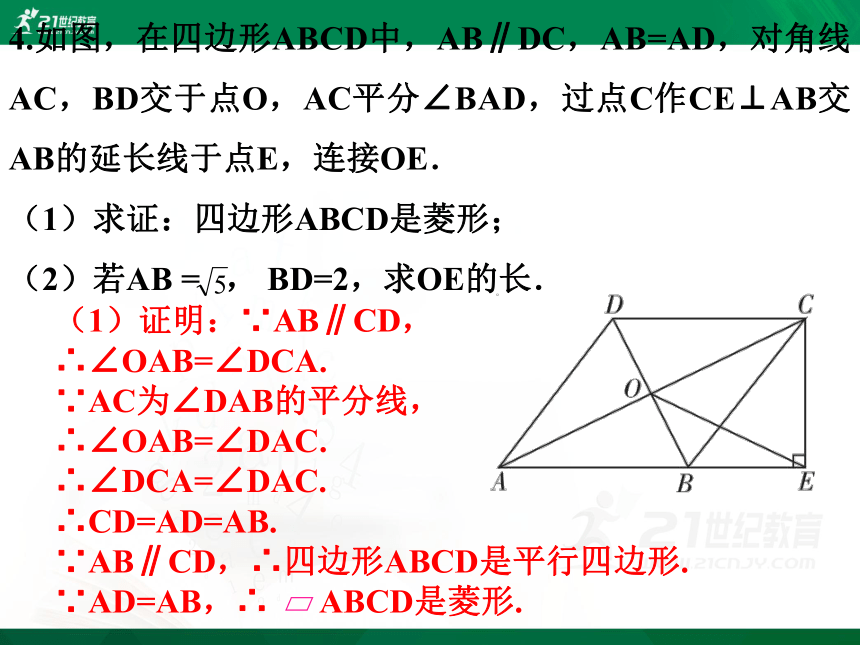
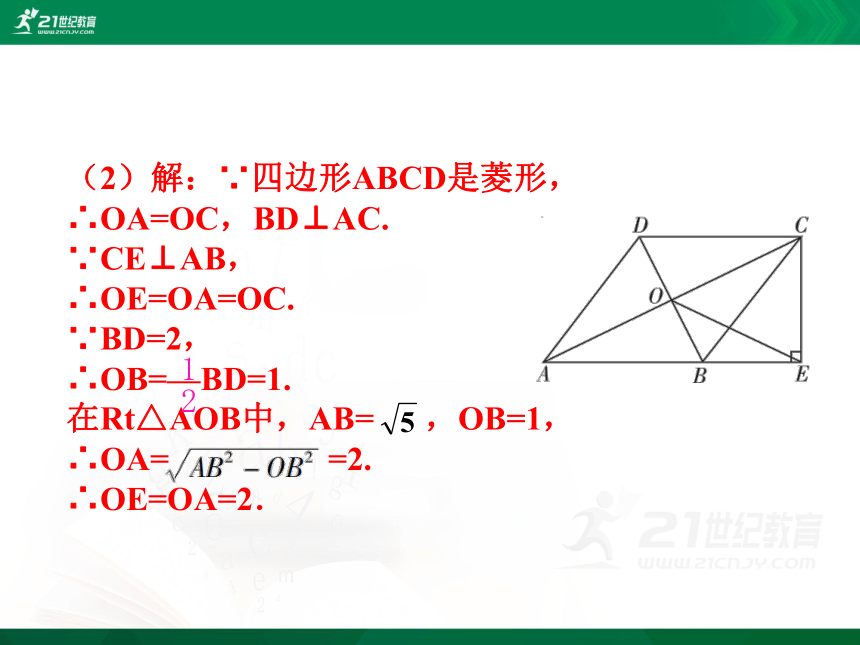
4.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB = , BD=2,求OE的长.
(1)证明:∵AB∥CD,
∴∠OAB=∠DCA.
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC.
∴∠DCA=∠DAC.
∴CD=AD=AB.
∵AB∥CD,∴四边形ABCD是平行四边形.
∵AD=AB,∴ ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC.
∵CE⊥AB,
∴OE=OA=OC.
∵BD=2,
∴OB=—BD=1.
在Rt△AOB中,AB= ,OB=1,
∴OA= =2.
∴OE=OA=2.
2
1
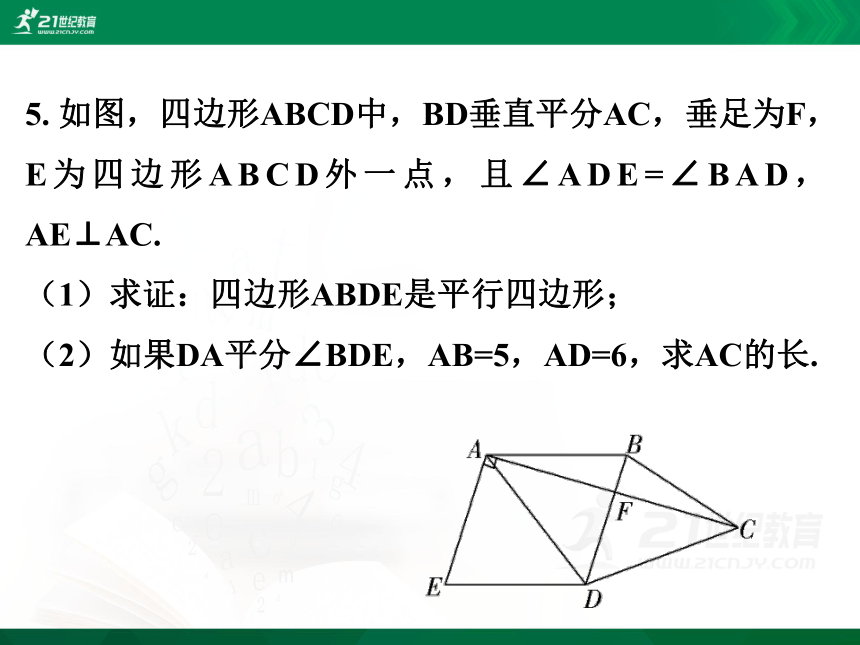
5. 如图,四边形ABCD中,BD垂直平分AC,垂足为F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
(1)证明:∵∠ADE=∠BAD,
∴AB∥DE.
∵AE⊥AC,BD⊥AC,∴AE∥BD.
∴四边形ABDE是平行四边形.
(2)解:∵DA平分∠BDE,
∴∠ADE=∠BDA.∴∠BAD=∠BDA.
∴BD=AB=5.
设BF=x,则DF=5-x,
∴AD2-DF2=AB2-BF2.
∴62-(5-x)2=52-x2.∴x= .
∴AF= =
∴AC=2AF= .
6. 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过D作DE∥BC交AB于点E,DF∥AB交BC于点F,连接EF.
(1)求证:四边形BFDE是菱形;
(2)若AB=8,AD=4,求BF的长.
(1)证明:∵DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形.
∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥BC,∴∠CBD=∠EDB.
∴∠ABD=∠EDB.
∴EB=ED.
∴平行四边形BFDE是菱形.
(2)解:∵ED∥BF,∠C=90°,
∴∠ADE=90°.
设BF=x,∴DE=BE=x. ∴AE=8-x.
在Rt△ADE中,AE2=DE2+AD2,
∴(8-x)2=x2+42.解得x=3.
∴BF=3.
1. 如图,在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE等于( )
A. 30° B. 22.5°
C. 15° D. 以上答案都不对
C
考点精析
(二)矩形的性质与判定
2. 如图,矩形ABCD中,对角线AC=2 ,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,点B恰好落在对角线AC上的B′处,则AB=_______.
3.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
(1)证明:∵AF∥BC,∴∠AFE=∠DCE.
∵E是AD的中点,∴AE=DE.
∵∠AEF=∠DEC,∴△AEF≌△DEC.
∴AF=DC.∵AF=BD.∴BD=CD.
∴D是BC的中点.
(2)解:四边形AFBD是矩形,
证明:∵AB=AC,D是BC的中点,
∴AD⊥BC.∴∠ADB=90°.
∵AF=BD,AF∥BC,
∴四边形AFBD是平行四边形.
∴四边形AFBD是矩形.
4.如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
(1)证明:∵AB∥CF,∴∠EAD=∠EFC,∠ADE=∠FCE.
∵E是CD的中点,∴DE=CE.
在△ADE和△FCE中,
∠DAE=∠EFC,∠ADE=∠ECF,DE=EC,
∴△ADE≌FCE(AAS).
∴AD=CF.
(2)解:四边形CDBF是矩形.
理由如下:∵AD=CF,CD是AB边上的中线,
∴AD=BD.∴BD=CF.
又∵BD∥CF,
∴四边形CDBF是平行四边形.
∵CA=CB,AD=BD,
∴CD⊥AB.∴∠CDB=90°.
∴四边形CDBF是矩形.
1. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是 ( )
A.
B.
C.
D.
A
考点精析
(三)正方形的性质与判定
2.如图,四边形ABCD中,对角线AC⊥BD,E,F,G,H分别是各边的中点,若AC=8,BD=6,
则四边形EFHG的面积是______.
12
3.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是________.
4.如图,在四边形ABCD中,AB=BC ,对角线BD平分∠ ABC ,P是BD上一点,过点P作PM ⊥ AD ,PN ⊥ CD ,垂足分别为M、N.
(1) 求证:∠ADB=∠CDB;
C
A
B
D
P
M
N
证明:∵BD平分∠ABC.
∴∠ABD=∠CBD.
∵ AB = BC, BD = BD
∴△ABD≌△CBD (AAS).
∴∠ADB=∠CDB.
4.如图,在四边形ABCD中,AB=BC ,对角线BD平分∠ ABC ,P是BD上一点,过点P作PM ⊥ AD ,PN ⊥ CD ,垂足分别为M、N.
(2) 若∠ADC=90°,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形
5. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
证明:∵四边形EFGA和四边形ABCD都是正方形,
∴AG=AE,AB=AD,∠DAB=90°, ∠EAG=90°
∵ ∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB.
在△GAD和△EAB中,
AG=AE,AB=AD,∴∠GAD=∠EAB.
∴△GAD≌△EAB(SAS).
∴EB=GD.
5. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(2)判断EB与GD的位置关系,并说明理由;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°.
∴∠AMB+∠ABM=90°.
又∵△AEB≌△AGD,
∴∠GDA=∠EBA.
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°.
∴∠DHM=180°-(∠HDM+∠DMH)=180°-90°=90°.
∴EB⊥GD.
5.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(3)若AB=2,AG= ,求EB的长.
解:连接AC,BD,BD与AC交于点O.
∵AB=AD=2,
在Rt△ABD中,DB= ,
在Rt△AOB中,OA=OB,AB=2,由勾股定理,得2AO2=22,OA= ,
即OG=OA+AG= + =2 ,
∴EB=GD= .
六、布置作业
课本P26 复习题
特殊平行四边形
专题复习
2020年秋北师大版九年级上册
思维导图
(一)平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
二、知识梳理
{5940675A-B579-460E-94D1-54222C63F5DA}
菱形
矩形
正方形
轴对称
轴对称图形
中心对称图形
轴对称图形
中心对称图形
边
对边平行,
四边都相等
对边平行
且相等
角
对角相等,
邻角互补
四个角
都是直角
对角线
对角线互相
垂直平分
对角线相等
且互相平分
轴对称图形
中心对称图形
对边平行
四条边相等
四个角
都是相等
对角线相等
互相垂直平分
(二)菱形、矩形、正方形的性质
二、知识梳理
四边形
条件
矩形
菱形
正方形
(三)菱形、矩形、正方形的判定
①定义:有一外角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形
有一个角是90°
(或对角线互相垂直)
有一对邻边相等
(或对角线相等)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)
有一个角是90°
对角线相等
有一对邻边相等
对角线互相垂直
(三)菱形、矩形、正方形的判定
1. 如图,在菱形ABCD中,过点A作AE⊥BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为 ( )
A. 12
B. 6
C.
D. 2
B
考点精析
(一)菱形的性质与判定
2. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为 ( )
A. 2 B. 3 C. D. 2
D
3. 如图,△ABC中,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,若AF=6,则四边形AEDF的周长是( )
A. 24 B. 28 C. 32 D. 36
A
4.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB = , BD=2,求OE的长.
(1)证明:∵AB∥CD,
∴∠OAB=∠DCA.
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC.
∴∠DCA=∠DAC.
∴CD=AD=AB.
∵AB∥CD,∴四边形ABCD是平行四边形.
∵AD=AB,∴ ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC.
∵CE⊥AB,
∴OE=OA=OC.
∵BD=2,
∴OB=—BD=1.
在Rt△AOB中,AB= ,OB=1,
∴OA= =2.
∴OE=OA=2.
2
1
5. 如图,四边形ABCD中,BD垂直平分AC,垂足为F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
(1)证明:∵∠ADE=∠BAD,
∴AB∥DE.
∵AE⊥AC,BD⊥AC,∴AE∥BD.
∴四边形ABDE是平行四边形.
(2)解:∵DA平分∠BDE,
∴∠ADE=∠BDA.∴∠BAD=∠BDA.
∴BD=AB=5.
设BF=x,则DF=5-x,
∴AD2-DF2=AB2-BF2.
∴62-(5-x)2=52-x2.∴x= .
∴AF= =
∴AC=2AF= .
6. 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过D作DE∥BC交AB于点E,DF∥AB交BC于点F,连接EF.
(1)求证:四边形BFDE是菱形;
(2)若AB=8,AD=4,求BF的长.
(1)证明:∵DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形.
∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥BC,∴∠CBD=∠EDB.
∴∠ABD=∠EDB.
∴EB=ED.
∴平行四边形BFDE是菱形.
(2)解:∵ED∥BF,∠C=90°,
∴∠ADE=90°.
设BF=x,∴DE=BE=x. ∴AE=8-x.
在Rt△ADE中,AE2=DE2+AD2,
∴(8-x)2=x2+42.解得x=3.
∴BF=3.
1. 如图,在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE等于( )
A. 30° B. 22.5°
C. 15° D. 以上答案都不对
C
考点精析
(二)矩形的性质与判定
2. 如图,矩形ABCD中,对角线AC=2 ,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,点B恰好落在对角线AC上的B′处,则AB=_______.
3.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
(1)证明:∵AF∥BC,∴∠AFE=∠DCE.
∵E是AD的中点,∴AE=DE.
∵∠AEF=∠DEC,∴△AEF≌△DEC.
∴AF=DC.∵AF=BD.∴BD=CD.
∴D是BC的中点.
(2)解:四边形AFBD是矩形,
证明:∵AB=AC,D是BC的中点,
∴AD⊥BC.∴∠ADB=90°.
∵AF=BD,AF∥BC,
∴四边形AFBD是平行四边形.
∴四边形AFBD是矩形.
4.如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
(1)证明:∵AB∥CF,∴∠EAD=∠EFC,∠ADE=∠FCE.
∵E是CD的中点,∴DE=CE.
在△ADE和△FCE中,
∠DAE=∠EFC,∠ADE=∠ECF,DE=EC,
∴△ADE≌FCE(AAS).
∴AD=CF.
(2)解:四边形CDBF是矩形.
理由如下:∵AD=CF,CD是AB边上的中线,
∴AD=BD.∴BD=CF.
又∵BD∥CF,
∴四边形CDBF是平行四边形.
∵CA=CB,AD=BD,
∴CD⊥AB.∴∠CDB=90°.
∴四边形CDBF是矩形.
1. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是 ( )
A.
B.
C.
D.
A
考点精析
(三)正方形的性质与判定
2.如图,四边形ABCD中,对角线AC⊥BD,E,F,G,H分别是各边的中点,若AC=8,BD=6,
则四边形EFHG的面积是______.
12
3.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是________.
4.如图,在四边形ABCD中,AB=BC ,对角线BD平分∠ ABC ,P是BD上一点,过点P作PM ⊥ AD ,PN ⊥ CD ,垂足分别为M、N.
(1) 求证:∠ADB=∠CDB;
C
A
B
D
P
M
N
证明:∵BD平分∠ABC.
∴∠ABD=∠CBD.
∵ AB = BC, BD = BD
∴△ABD≌△CBD (AAS).
∴∠ADB=∠CDB.
4.如图,在四边形ABCD中,AB=BC ,对角线BD平分∠ ABC ,P是BD上一点,过点P作PM ⊥ AD ,PN ⊥ CD ,垂足分别为M、N.
(2) 若∠ADC=90°,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形
5. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
证明:∵四边形EFGA和四边形ABCD都是正方形,
∴AG=AE,AB=AD,∠DAB=90°, ∠EAG=90°
∵ ∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB.
在△GAD和△EAB中,
AG=AE,AB=AD,∴∠GAD=∠EAB.
∴△GAD≌△EAB(SAS).
∴EB=GD.
5. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(2)判断EB与GD的位置关系,并说明理由;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°.
∴∠AMB+∠ABM=90°.
又∵△AEB≌△AGD,
∴∠GDA=∠EBA.
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°.
∴∠DHM=180°-(∠HDM+∠DMH)=180°-90°=90°.
∴EB⊥GD.
5.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(3)若AB=2,AG= ,求EB的长.
解:连接AC,BD,BD与AC交于点O.
∵AB=AD=2,
在Rt△ABD中,DB= ,
在Rt△AOB中,OA=OB,AB=2,由勾股定理,得2AO2=22,OA= ,
即OG=OA+AG= + =2 ,
∴EB=GD= .
六、布置作业
课本P26 复习题
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
