北师大版九年级上册数学第三章 概率的进一步认识专题训练 小专题(三) 概率计算的技巧(Word版 含答案)
文档属性
| 名称 | 北师大版九年级上册数学第三章 概率的进一步认识专题训练 小专题(三) 概率计算的技巧(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 95.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 00:00:00 | ||
图片预览

文档简介
北师大版九年级上册数学专题训练
小专题(三) 概率计算的技巧
【专题概述】
概率是通过大量重复试验中频率的稳定性得到的一个0~1的常数,它反映了事件发生的可能性的大小.需要注意的是:概率是针对大量重复试验而言的,大量重复试验反映的规律并不一定出现在每次试验中.常见的计算概率的方法有公式法(仅适用于等可能事件)、列表法、画树状图法和频率估算法等.
类型1 两步完成的事件的概率
两步完成的事件的概率,既可以用列表法来求(列表法只适合于两步完成的事件的概率),也可以用树状图法来求(树状图法适合于两步完成及两步以上完成的事件的概率).
1.某校举行以“激情五月,唱响青春”为主题的演讲比赛.决赛阶段只剩下甲、乙、丙、丁四名同学,则甲、乙同学得前两名的概率是
(
)
A.
B.
C.
D.
2.小明从一副扑克牌中取出3张红桃、2张黑桃共5张牌与弟弟做游戏,把这5张牌背面朝上洗匀后放在桌子上,小明与弟弟同时各抽一张,则两人抽到花色相同的概率是
(
)
A.
B.
C.
D.
3.袋内装有标号分别为1,2,3,4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为
(
)
A.
B.
C.
D.
4.点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是?
.?
5.随着信息化时代的到来,微信支付、支付宝支付、QQ红包支付、银行卡支付等各种便捷支付已经成为我们生活中的一部分.某学校某宿舍的5名同学,有3人使用微信支付,2人使用支付宝支付,则从这5人中随机抽出两人,他们使用同一种支付方式的概率是?
.?
6.某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n/本
1
2
3
4
5
6
7
8
9
人数/名
1
2
6
7
12
x
7
y
1
请根据以上信息回答下列问题:
(1)分别求出统计表中的x,y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
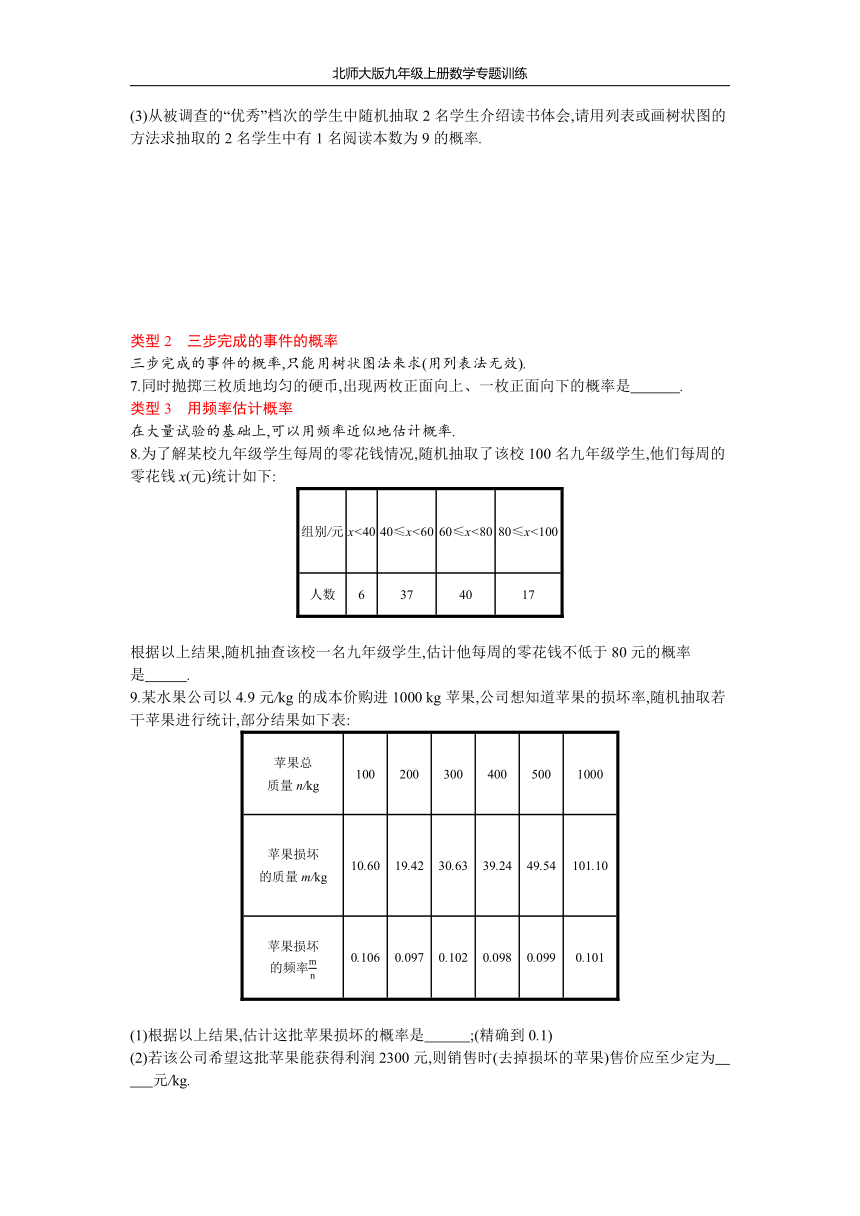
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
类型2 三步完成的事件的概率
三步完成的事件的概率,只能用树状图法来求(用列表法无效).
7.同时抛掷三枚质地均匀的硬币,出现两枚正面向上、一枚正面向下的概率是?
.?
类型3 用频率估计概率
在大量试验的基础上,可以用频率近似地估计概率.
8.为了解某校九年级学生每周的零花钱情况,随机抽取了该校100名九年级学生,他们每周的零花钱x(元)统计如下:
组别/元
x<40
40≤x<60
60≤x<80
80≤x<100
人数
6
37
40
17
根据以上结果,随机抽查该校一名九年级学生,估计他每周的零花钱不低于80元的概率是?
.?
9.某水果公司以4.9元/kg的成本价购进1000
kg苹果,公司想知道苹果的损坏率,随机抽取若干苹果进行统计,部分结果如下表:
苹果总
质量n/kg
100
200
300
400
500
1000
苹果损坏
的质量m/kg
10.60
19.42
30.63
39.24
49.54
101.10
苹果损坏
的频率
0.106
0.097
0.102
0.098
0.099
0.101
(1)根据以上结果,估计这批苹果损坏的概率是
;(精确到0.1)?
(2)若该公司希望这批苹果能获得利润2300元,则销售时(去掉损坏的苹果)售价应至少定为 8 元/kg.?
类型4 几何概型
几何概型也就是概率的大小与面积大小有关,事件发生的概率等于此事件所有可能结果组成的图形面积除以所有可能结果组成的图形面积.
10.一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状、大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为?
.?
类型5 判断游戏的公平性等概率的综合应用
通过计算概率判断游戏是不是公平的是概率知识的一个重要应用,也是中考考查的热点.解决游戏问题要先计算游戏双方获胜的概率,若概率相等,则游戏公平;若概率不相等,则游戏不公平.
11.小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转).这个游戏对双方公平吗?请用树状图或列表法说明理由.
12.一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
参考答案
1.
(D)
2.
(D)
3.
(B)
4.?
5.?
6.解:(1)由表可知被调查学生中“一般”档次的有13人,所占比例是26%,
∴共调查的学生数是13÷26%=50,
∴调查学生中“良好”档次的人数为50×60%=30,
∴x=30-(12+7)=11,
y=50-(1+2+6+7+12+11+7+1)=3.
(2)由样本数据可知“优秀”档次所占的百分比为=8%,
∴估计九年级400名学生中为“优秀”档次的人数为400×8%=32.
(3)用A,B,C表示阅读本数是8的学生,用D表示阅读本数是9的学生,画树状图如下:
由树状图可知,共有12种等可能的结果,其中所抽取的2名学生中有1名阅读本数为9的结果有6种,
所以抽取的2名学生中有1名阅读本数为9的概率为.
7.?
8.?
9.
(1) 0.1
(2) 8
10.?
11.解:这个游戏对双方是公平的.画树状图如下:
由树状图可知一共有6种情况,和小于4的结果有3种,
∴P(和小于4)=,∴这个游戏对双方是公平的.
12.解:(1)袋中白球的个数为290×=10,
红球和黑球总数为290-10=280,
黑球的个数为(280-40)÷(2+1)=80,
红球的个数为280-80=200,
所以袋中红球的个数是200.
(2)80÷290=,
所以从袋中任取一个球是黑球的概率是.
小专题(三) 概率计算的技巧
【专题概述】
概率是通过大量重复试验中频率的稳定性得到的一个0~1的常数,它反映了事件发生的可能性的大小.需要注意的是:概率是针对大量重复试验而言的,大量重复试验反映的规律并不一定出现在每次试验中.常见的计算概率的方法有公式法(仅适用于等可能事件)、列表法、画树状图法和频率估算法等.
类型1 两步完成的事件的概率
两步完成的事件的概率,既可以用列表法来求(列表法只适合于两步完成的事件的概率),也可以用树状图法来求(树状图法适合于两步完成及两步以上完成的事件的概率).
1.某校举行以“激情五月,唱响青春”为主题的演讲比赛.决赛阶段只剩下甲、乙、丙、丁四名同学,则甲、乙同学得前两名的概率是
(
)
A.
B.
C.
D.
2.小明从一副扑克牌中取出3张红桃、2张黑桃共5张牌与弟弟做游戏,把这5张牌背面朝上洗匀后放在桌子上,小明与弟弟同时各抽一张,则两人抽到花色相同的概率是
(
)
A.
B.
C.
D.
3.袋内装有标号分别为1,2,3,4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为
(
)
A.
B.
C.
D.
4.点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是?
.?
5.随着信息化时代的到来,微信支付、支付宝支付、QQ红包支付、银行卡支付等各种便捷支付已经成为我们生活中的一部分.某学校某宿舍的5名同学,有3人使用微信支付,2人使用支付宝支付,则从这5人中随机抽出两人,他们使用同一种支付方式的概率是?
.?
6.某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n/本
1
2
3
4
5
6
7
8
9
人数/名
1
2
6
7
12
x
7
y
1
请根据以上信息回答下列问题:
(1)分别求出统计表中的x,y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
类型2 三步完成的事件的概率
三步完成的事件的概率,只能用树状图法来求(用列表法无效).
7.同时抛掷三枚质地均匀的硬币,出现两枚正面向上、一枚正面向下的概率是?
.?
类型3 用频率估计概率
在大量试验的基础上,可以用频率近似地估计概率.
8.为了解某校九年级学生每周的零花钱情况,随机抽取了该校100名九年级学生,他们每周的零花钱x(元)统计如下:
组别/元
x<40
40≤x<60
60≤x<80
80≤x<100
人数
6
37
40
17
根据以上结果,随机抽查该校一名九年级学生,估计他每周的零花钱不低于80元的概率是?
.?
9.某水果公司以4.9元/kg的成本价购进1000
kg苹果,公司想知道苹果的损坏率,随机抽取若干苹果进行统计,部分结果如下表:
苹果总
质量n/kg
100
200
300
400
500
1000
苹果损坏
的质量m/kg
10.60
19.42
30.63
39.24
49.54
101.10
苹果损坏
的频率
0.106
0.097
0.102
0.098
0.099
0.101
(1)根据以上结果,估计这批苹果损坏的概率是
;(精确到0.1)?
(2)若该公司希望这批苹果能获得利润2300元,则销售时(去掉损坏的苹果)售价应至少定为 8 元/kg.?
类型4 几何概型
几何概型也就是概率的大小与面积大小有关,事件发生的概率等于此事件所有可能结果组成的图形面积除以所有可能结果组成的图形面积.
10.一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状、大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为?
.?
类型5 判断游戏的公平性等概率的综合应用
通过计算概率判断游戏是不是公平的是概率知识的一个重要应用,也是中考考查的热点.解决游戏问题要先计算游戏双方获胜的概率,若概率相等,则游戏公平;若概率不相等,则游戏不公平.
11.小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转).这个游戏对双方公平吗?请用树状图或列表法说明理由.
12.一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
参考答案
1.
(D)
2.
(D)
3.
(B)
4.?
5.?
6.解:(1)由表可知被调查学生中“一般”档次的有13人,所占比例是26%,
∴共调查的学生数是13÷26%=50,
∴调查学生中“良好”档次的人数为50×60%=30,
∴x=30-(12+7)=11,
y=50-(1+2+6+7+12+11+7+1)=3.
(2)由样本数据可知“优秀”档次所占的百分比为=8%,
∴估计九年级400名学生中为“优秀”档次的人数为400×8%=32.
(3)用A,B,C表示阅读本数是8的学生,用D表示阅读本数是9的学生,画树状图如下:
由树状图可知,共有12种等可能的结果,其中所抽取的2名学生中有1名阅读本数为9的结果有6种,
所以抽取的2名学生中有1名阅读本数为9的概率为.
7.?
8.?
9.
(1) 0.1
(2) 8
10.?
11.解:这个游戏对双方是公平的.画树状图如下:
由树状图可知一共有6种情况,和小于4的结果有3种,
∴P(和小于4)=,∴这个游戏对双方是公平的.
12.解:(1)袋中白球的个数为290×=10,
红球和黑球总数为290-10=280,
黑球的个数为(280-40)÷(2+1)=80,
红球的个数为280-80=200,
所以袋中红球的个数是200.
(2)80÷290=,
所以从袋中任取一个球是黑球的概率是.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
