人教版九年级数学上册 23.2.1中心对称图形 上课课件(23张)
文档属性
| 名称 | 人教版九年级数学上册 23.2.1中心对称图形 上课课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 21:45:19 | ||
图片预览






文档简介
(共23张PPT)
23.2
中心对称
23.2.1
中心对称
人教版
数学
九年级
上册
新课导入
导入课题
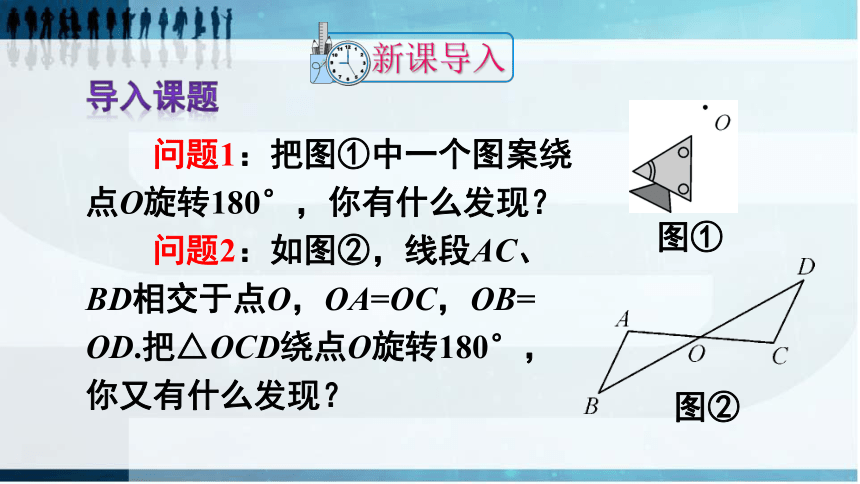
问题1:把图①中一个图案绕点O旋转180°,你有什么发现?
问题2:如图②,线段AC、BD相交于点O,OA=OC,OB=
OD.把△OCD绕点O旋转180°,你又有什么发现?
图①
图②
【学习目标】
1.认识两个图形关于某一点中心对称的本质.
2.理解中心对称的性质,并可以判断两个图形是否成中心对称.
3.会画某图形关于某点对称的图形,会确定对称中心.
【学习重点】
判断两个图形是否成中心对称.
【学习难点】
画某图形关于某点对称的图形,确定对称中心.
推进新课
知识点1
中心对称及其相关概念
问题1:把图①中一个图案绕点O旋转180°,你有什么发现?
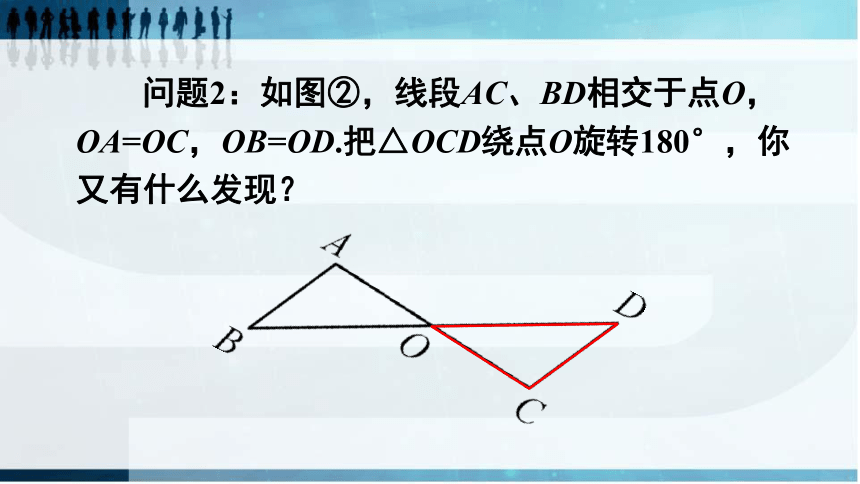
问题2:如图②,线段AC、BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你又有什么发现?
你发现了什么?
把一个图形
,如果它
,那么就说这两个图形关于这个点
或
,这个点叫做
.
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
中心对称是指几个图形之间的位置关系?一个图形绕一点旋转能与另一个图形重合就是中心对称吗?
两个.
不一定,必须是绕一点旋转180°能与另一个图形重合才是中心对称.
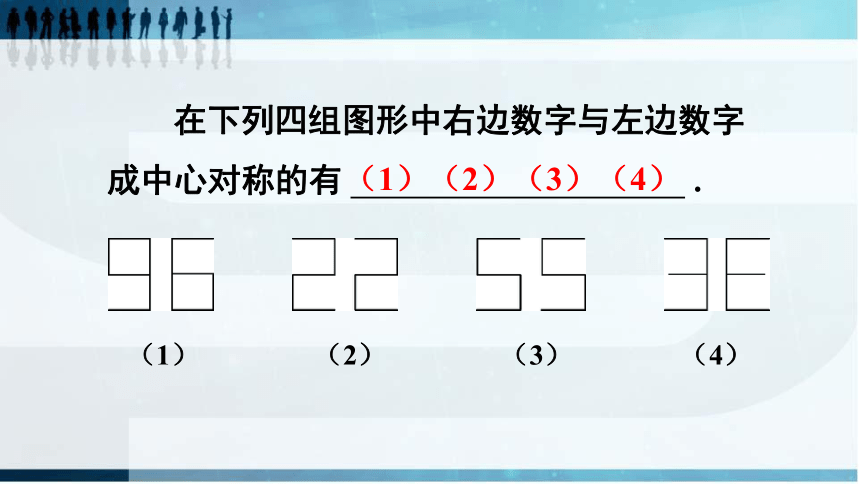
在下列四组图形中右边数字与左边数字成中心对称的有
.
(1)
(2)
(3)
(4)
(1)(2)(3)(4)
思考:两个图形成中心对称需要具备什么条件?
两个图形成中心对称须具备三个条件:
①能找到一个对称中心;
②旋转角为180°;
③这两个图形旋转后能重合.
按下列步骤动手画图:
第一步:用三角尺画出△ABC;
第二步:以三角尺的一个顶点O为中心,把三角尺旋转180°,再画出△A′B′C′;
第三步:移开三角尺,并用虚线连接对应点A、A′,B、B′,C、C′.
知识点2
中心对称的性质
第一步
第二步
第三步
a.
△ABC与△A′B′C′关于点O对称吗?
对称.
b.
△ABC与△A′B′C′全等吗?为什么?
全等.由图形旋转的性质可知△ABC≌△A′B′C′.
c.
线段AA′、BB′、CC′有何关系?
相交于点O.
d.
点O在线段AA′、BB′、CC′的什么位置?
点O在线段AA′、BB′、CC′的中点处.
中心对称的性质
中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
中心对称的两个图形是全等图形.
A′
①怎样画点A关于点O的对称点?
连接AO,在AO的延长线上截取OA′=OA,即可求得点A关于点O的对称点A′.
②怎样画△ABC关于点O对称的△A′B′C′?
作出A,B,C三点关于点O的对称点A′,B′,C′,依次连接A′B′,B′C′,C′A′,就可得到与
△ABC关于点O对称的△A′B′C′.
A′
B′
C′
随堂演练
1.
下列结论中,错误的是(
)
A.形状大小完全相同的两个图形一定关于某点成中心对称
B.成中心对称的两个图形,对称中心到两对称点的距离相等
C.成中心对称的两图形,对称中心在两对称点的连线上
D.成中心对称的两图形,对应线段平行(或在同一直线上)且相等
A
2.
如图,△ABC与△A1B1C1关于点O成中心对称,下
列说法:①∠BAC=∠B1A1C1;②AC=A1C1;
③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有(
)
?
A.1个
B.2个
C.3个
D.4个
D
3.
如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是(
)
A.AD∥EF,AB∥GF
B.BO=GO
C.CD=HE,BC=GH
D.DO=HO
D
G
4.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形
(2)S四边形ABFE=4S△ABC=12
cm2.
课堂小结
中心对称
概念
性质
绕着某一点旋转180°
能够与另一个图形重合
对称点所连线段都经过对称中心,而且被对称中心所平分.
中心对称的两个图形是全等图形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
教学反思
本课设计通过问题导入,遵循从感性到理性的渐进认识规律、发展学生直观想象能力,分析、归纳、抽象概括的思维能力.学生在探究新知的过程中,教师给予学生更多的互动时间,联系生活中的例子,让学生对知识易于理解,易于接受.教学过程中要强调中心对称的性质和利用中心对称的性质作图的方法.从课堂发言和练习来看,学生积极动手动脑,教师适当引导,学生成为课堂的主人.
23.2
中心对称
23.2.1
中心对称
人教版
数学
九年级
上册
新课导入
导入课题
问题1:把图①中一个图案绕点O旋转180°,你有什么发现?
问题2:如图②,线段AC、BD相交于点O,OA=OC,OB=
OD.把△OCD绕点O旋转180°,你又有什么发现?
图①
图②
【学习目标】
1.认识两个图形关于某一点中心对称的本质.
2.理解中心对称的性质,并可以判断两个图形是否成中心对称.
3.会画某图形关于某点对称的图形,会确定对称中心.
【学习重点】
判断两个图形是否成中心对称.
【学习难点】
画某图形关于某点对称的图形,确定对称中心.
推进新课
知识点1
中心对称及其相关概念
问题1:把图①中一个图案绕点O旋转180°,你有什么发现?
问题2:如图②,线段AC、BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你又有什么发现?
你发现了什么?
把一个图形
,如果它
,那么就说这两个图形关于这个点
或
,这个点叫做
.
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
中心对称是指几个图形之间的位置关系?一个图形绕一点旋转能与另一个图形重合就是中心对称吗?
两个.
不一定,必须是绕一点旋转180°能与另一个图形重合才是中心对称.
在下列四组图形中右边数字与左边数字成中心对称的有
.
(1)
(2)
(3)
(4)
(1)(2)(3)(4)
思考:两个图形成中心对称需要具备什么条件?
两个图形成中心对称须具备三个条件:
①能找到一个对称中心;
②旋转角为180°;
③这两个图形旋转后能重合.
按下列步骤动手画图:
第一步:用三角尺画出△ABC;
第二步:以三角尺的一个顶点O为中心,把三角尺旋转180°,再画出△A′B′C′;
第三步:移开三角尺,并用虚线连接对应点A、A′,B、B′,C、C′.
知识点2
中心对称的性质
第一步
第二步
第三步
a.
△ABC与△A′B′C′关于点O对称吗?
对称.
b.
△ABC与△A′B′C′全等吗?为什么?
全等.由图形旋转的性质可知△ABC≌△A′B′C′.
c.
线段AA′、BB′、CC′有何关系?
相交于点O.
d.
点O在线段AA′、BB′、CC′的什么位置?
点O在线段AA′、BB′、CC′的中点处.
中心对称的性质
中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
中心对称的两个图形是全等图形.
A′
①怎样画点A关于点O的对称点?
连接AO,在AO的延长线上截取OA′=OA,即可求得点A关于点O的对称点A′.
②怎样画△ABC关于点O对称的△A′B′C′?
作出A,B,C三点关于点O的对称点A′,B′,C′,依次连接A′B′,B′C′,C′A′,就可得到与
△ABC关于点O对称的△A′B′C′.
A′
B′
C′
随堂演练
1.
下列结论中,错误的是(
)
A.形状大小完全相同的两个图形一定关于某点成中心对称
B.成中心对称的两个图形,对称中心到两对称点的距离相等
C.成中心对称的两图形,对称中心在两对称点的连线上
D.成中心对称的两图形,对应线段平行(或在同一直线上)且相等
A
2.
如图,△ABC与△A1B1C1关于点O成中心对称,下
列说法:①∠BAC=∠B1A1C1;②AC=A1C1;
③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有(
)
?
A.1个
B.2个
C.3个
D.4个
D
3.
如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是(
)
A.AD∥EF,AB∥GF
B.BO=GO
C.CD=HE,BC=GH
D.DO=HO
D
G
4.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形
(2)S四边形ABFE=4S△ABC=12
cm2.
课堂小结
中心对称
概念
性质
绕着某一点旋转180°
能够与另一个图形重合
对称点所连线段都经过对称中心,而且被对称中心所平分.
中心对称的两个图形是全等图形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
教学反思
本课设计通过问题导入,遵循从感性到理性的渐进认识规律、发展学生直观想象能力,分析、归纳、抽象概括的思维能力.学生在探究新知的过程中,教师给予学生更多的互动时间,联系生活中的例子,让学生对知识易于理解,易于接受.教学过程中要强调中心对称的性质和利用中心对称的性质作图的方法.从课堂发言和练习来看,学生积极动手动脑,教师适当引导,学生成为课堂的主人.
同课章节目录
