人教版九年级数学上册 23.2.2中心对称图形 上课课件(21张)
文档属性
| 名称 | 人教版九年级数学上册 23.2.2中心对称图形 上课课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 21:48:37 | ||
图片预览






文档简介
(共21张PPT)
23.2.2
中心对称图形
R·九年级上册
新课导入
导入课题
猜一猜:
(1)如果将线段AB绕它的中点O旋转180°,会出现什么情况?
(2)如果将平行四边形ABCD绕它的两条对角线的交点O旋转180°,又会出现什么情况?
学习目标
学习重点
学习难点
(1)能判断一个图形是不是中心对称图形.
(2)知道中心对称和中心对称图形的区别和联系.
中心对称图形的概念.
中心对称和中心对称图形的区别和联系.
推进新课
知识点1
中心对称图形的概念
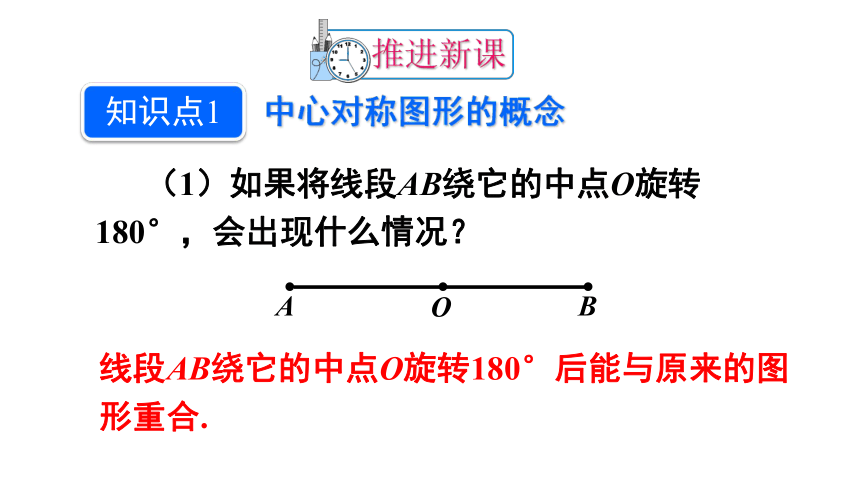
(1)如果将线段AB绕它的中点O旋转180°,会出现什么情况?
A
B
O
线段AB绕它的中点O旋转180°后能与原来的图形重合.
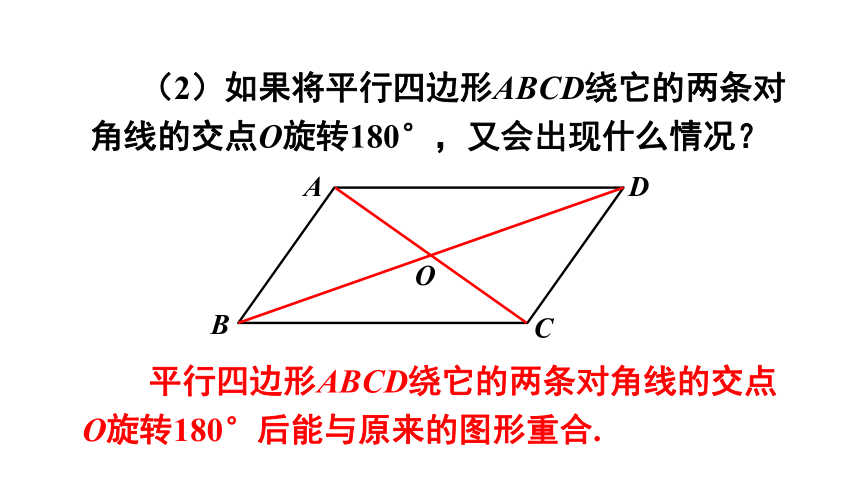
(2)如果将平行四边形ABCD绕它的两条对角线的交点O旋转180°,又会出现什么情况?
A
B
C
D
O
平行四边形ABCD绕它的两条对角线的交点O旋转180°后能与原来的图形重合.
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.
中心对称图形
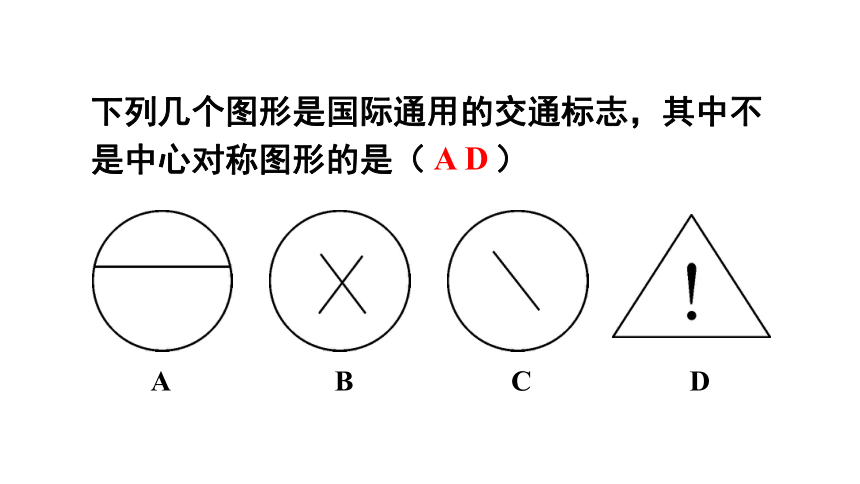
下列几个图形是国际通用的交通标志,其中不是中心对称图形的是(
)
A
B
C
D
A
D
知识点2
中心对称与中心对称图形的区别与联系
比较中心对称和中心对称图形的概念,试说明它们有何区别与联系.
区别:中心对称是针对两个图形而言的,而中心对称图形是针对单个图形而言的.
联系:如果把成中心对称的两个图形看成一个整体,则该图形为中心对称图形;如果把一个中心对称图形相互对称的两部分看成两个图形,则它们成中心对称.
你能设计出中心对称图形吗?
指出如图所示的汽车标志中的中心对称图形.
√
√
×
×
×
随堂演练
1.
下列图形中,既是轴对称图形,又是中心对
称图形的是(
)
A.等边三角形
B.等腰三角形
C.平行四边形
D.正方形
2.
下列图形中,是中心对称图形,但不一定是
轴对称图形的是(
)
A.正方形
B.矩形
C.菱形
D.平行四边形
D
D
3.
小明把如图(1)所示的扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌倒过来,如图(2),然后小明很快辨认出被倒过来的那张扑克牌是(
)
?
A.方块5
B.梅花6
C.红桃7
D.黑桃8
A
图(1)
图(2)
4.下列标志中,可以看做是中心对称图形的是(
)
D
5.
将两个大小相等的圆部分重合,其中重叠的部分
(如下图中的阴影部分)我们称之为一个“花瓣”,
由一个“花瓣”及圆组成的图形称之为花瓣图形,
下面是一些由“花瓣”和圆组成的图形.
A
B
C
D
E
二瓣
三瓣
四瓣
五瓣
六瓣
(1)以上5个图形中是轴对称图形的有
,是中心对称图形的有
;(分别用图形的代号A、B、C、D、E填空)
(2)若“花瓣”在圆中是均匀分布的,试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律:
“花瓣”个数为偶数时,这个图形既是轴对称图形又是中心对称图形;“花瓣”个数为奇数时,这个图形是轴对称图形.
A
B
C
D
E
A
C
E
(3)根据上面的结论,试判断下列花瓣图形的对称性:
①2014瓣图是
;
②2015瓣图形是
.
中心对称图形,也是轴对称图形
轴对称图形
课堂小结
中心对称是针对两个图形而言的,中心对称图形是针对一个图形而言的.
把一个图形绕着某一个点旋转180°后,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
教学反思
在创设情境环节中,实物图形把学生引入到丰富多彩的美丽世界,使学生享受了数学带给他们的快乐;在教学过程中,通过辨别中心对称图形,使学生产生了亲切的感受,教师强调:能判断常见的几何图形是不是中心对称图形,整节课的学习都是享受美的过程,接受美的熏陶,发现美,从而阐述自己的感受.
23.2.2
中心对称图形
R·九年级上册
新课导入
导入课题
猜一猜:
(1)如果将线段AB绕它的中点O旋转180°,会出现什么情况?
(2)如果将平行四边形ABCD绕它的两条对角线的交点O旋转180°,又会出现什么情况?
学习目标
学习重点
学习难点
(1)能判断一个图形是不是中心对称图形.
(2)知道中心对称和中心对称图形的区别和联系.
中心对称图形的概念.
中心对称和中心对称图形的区别和联系.
推进新课
知识点1
中心对称图形的概念
(1)如果将线段AB绕它的中点O旋转180°,会出现什么情况?
A
B
O
线段AB绕它的中点O旋转180°后能与原来的图形重合.
(2)如果将平行四边形ABCD绕它的两条对角线的交点O旋转180°,又会出现什么情况?
A
B
C
D
O
平行四边形ABCD绕它的两条对角线的交点O旋转180°后能与原来的图形重合.
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.
中心对称图形
下列几个图形是国际通用的交通标志,其中不是中心对称图形的是(
)
A
B
C
D
A
D
知识点2
中心对称与中心对称图形的区别与联系
比较中心对称和中心对称图形的概念,试说明它们有何区别与联系.
区别:中心对称是针对两个图形而言的,而中心对称图形是针对单个图形而言的.
联系:如果把成中心对称的两个图形看成一个整体,则该图形为中心对称图形;如果把一个中心对称图形相互对称的两部分看成两个图形,则它们成中心对称.
你能设计出中心对称图形吗?
指出如图所示的汽车标志中的中心对称图形.
√
√
×
×
×
随堂演练
1.
下列图形中,既是轴对称图形,又是中心对
称图形的是(
)
A.等边三角形
B.等腰三角形
C.平行四边形
D.正方形
2.
下列图形中,是中心对称图形,但不一定是
轴对称图形的是(
)
A.正方形
B.矩形
C.菱形
D.平行四边形
D
D
3.
小明把如图(1)所示的扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌倒过来,如图(2),然后小明很快辨认出被倒过来的那张扑克牌是(
)
?
A.方块5
B.梅花6
C.红桃7
D.黑桃8
A
图(1)
图(2)
4.下列标志中,可以看做是中心对称图形的是(
)
D
5.
将两个大小相等的圆部分重合,其中重叠的部分
(如下图中的阴影部分)我们称之为一个“花瓣”,
由一个“花瓣”及圆组成的图形称之为花瓣图形,
下面是一些由“花瓣”和圆组成的图形.
A
B
C
D
E
二瓣
三瓣
四瓣
五瓣
六瓣
(1)以上5个图形中是轴对称图形的有
,是中心对称图形的有
;(分别用图形的代号A、B、C、D、E填空)
(2)若“花瓣”在圆中是均匀分布的,试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律:
“花瓣”个数为偶数时,这个图形既是轴对称图形又是中心对称图形;“花瓣”个数为奇数时,这个图形是轴对称图形.
A
B
C
D
E
A
C
E
(3)根据上面的结论,试判断下列花瓣图形的对称性:
①2014瓣图是
;
②2015瓣图形是
.
中心对称图形,也是轴对称图形
轴对称图形
课堂小结
中心对称是针对两个图形而言的,中心对称图形是针对一个图形而言的.
把一个图形绕着某一个点旋转180°后,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
教学反思
在创设情境环节中,实物图形把学生引入到丰富多彩的美丽世界,使学生享受了数学带给他们的快乐;在教学过程中,通过辨别中心对称图形,使学生产生了亲切的感受,教师强调:能判断常见的几何图形是不是中心对称图形,整节课的学习都是享受美的过程,接受美的熏陶,发现美,从而阐述自己的感受.
同课章节目录
