人教版九年级数学上册 第二十三章 旋转 章末复习 课件(20张)
文档属性
| 名称 | 人教版九年级数学上册 第二十三章 旋转 章末复习 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 226.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
第二十三章 旋 转
复习课
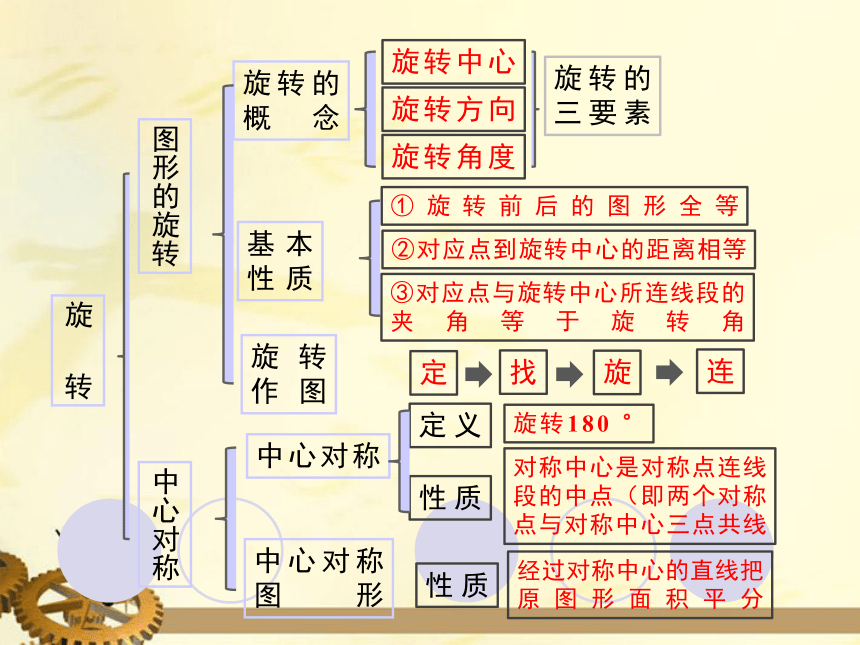
旋转的概念
旋转中心
旋转方向
旋转角度
旋转的三要素
基本
性质
①旋转前后的图形全等
②对应点到旋转中心的距离相等
旋 转
图形的旋转
③对应点与旋转中心所连线段的夹角等于旋转角
旋转
作图
定
找
旋
连
中心对称
中心对称
定义
旋转180 °
性质
对称中心是对称点连线段的中点(即两个对称点与对称中心三点共线
中心对称图形
性质
经过对称中心的直线把原图形面积平分
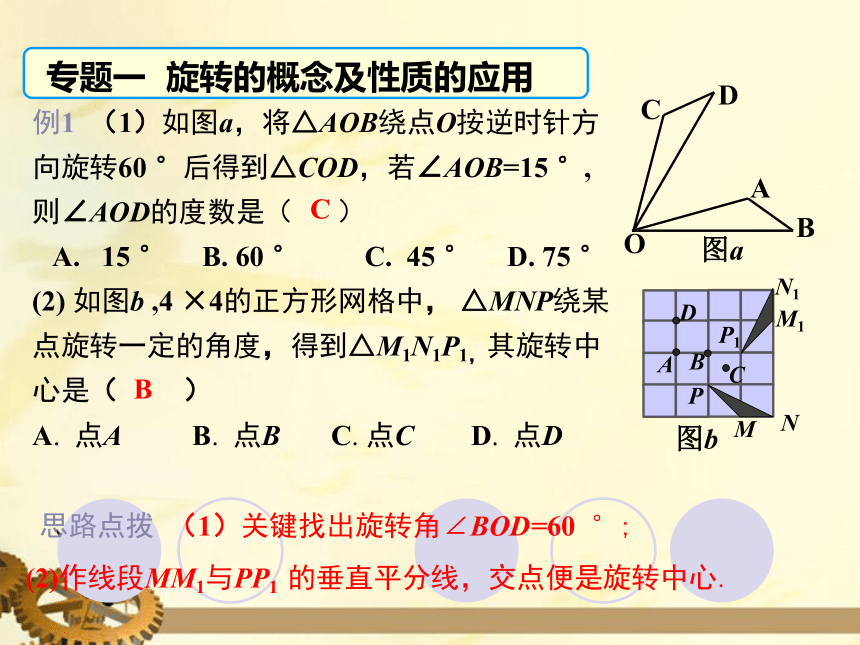
专题一 旋转的概念及性质的应用
例1 (1)如图a,将△AOB绕点O按逆时针方
向旋转60 °后得到△COD,若∠AOB=15 °,
则∠AOD的度数是( )
A. 15 ° B. 60 ° C. 45 ° D. 75 °
(2) 如图b ,4 ×4的正方形网格中, △MNP绕某
点旋转一定的角度,得到△M1N1P1,其旋转中
心是( )
A. 点A B. 点B C. 点C D. 点D
A
B
O
D
C
图a
C
N1
M1
N
M
P1
D
P
A
B
图b
C
B
思路点拨 (1)关键找出旋转角∠BOD=60 °;
(2)作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
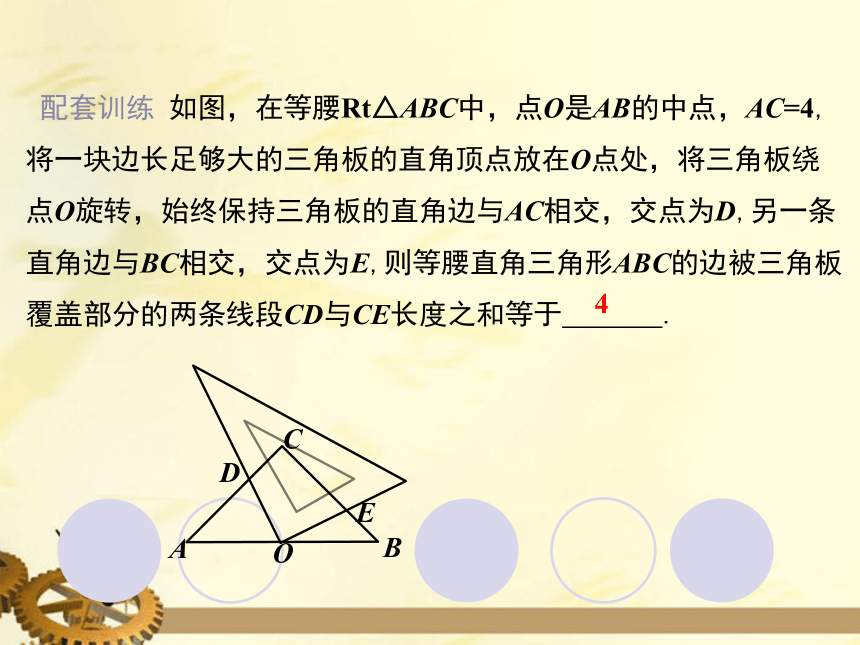
配套训练 如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 .
A
B
C
D
E
O
4
方法指导 中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
配套训练 下列说法不正确的是( )
A.任何一个具有对称中心的四边形都是平行四边形
B.平行四边形既是轴对称图形,又是中心对称图形
C.线段、平行四边形、矩形、菱形、正方形都是中心对称图形
D.正三角形、矩形、菱形、正方形都是轴对称图形,且对称轴都不止一条.
B
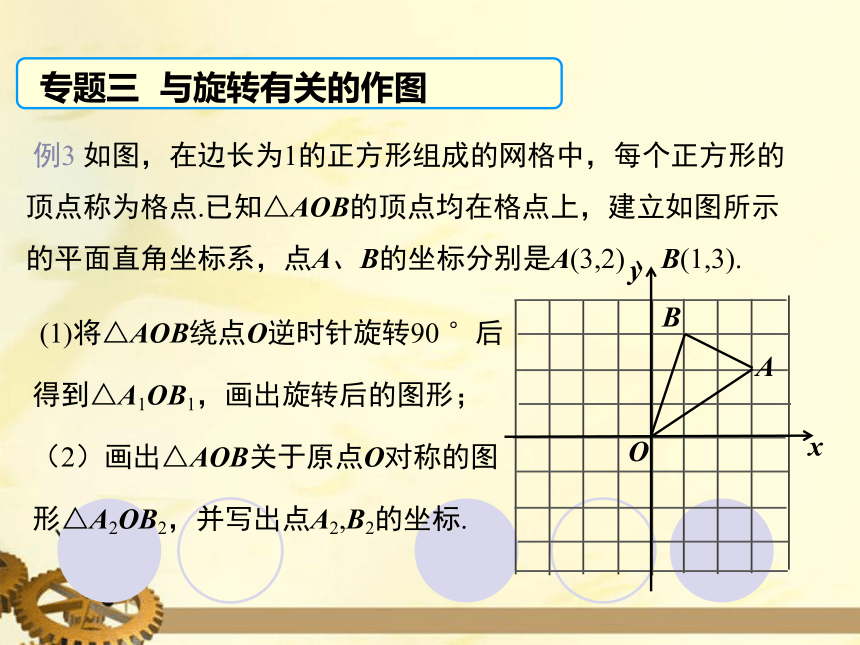
专题三 与旋转有关的作图
例3 如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△AOB的顶点均在格点上,建立如图所示的平面直角坐标系,点A、B的坐标分别是A(3,2) 、B(1,3).
x
y
O
A
B
(1)将△AOB绕点O逆时针旋转90 °后得到△A1OB1,画出旋转后的图形;
(2)画出△AOB关于原点O对称的图形△A2OB2,并写出点A2,B2的坐标.
x
y
O
A
B
A1
B1
A2
B2
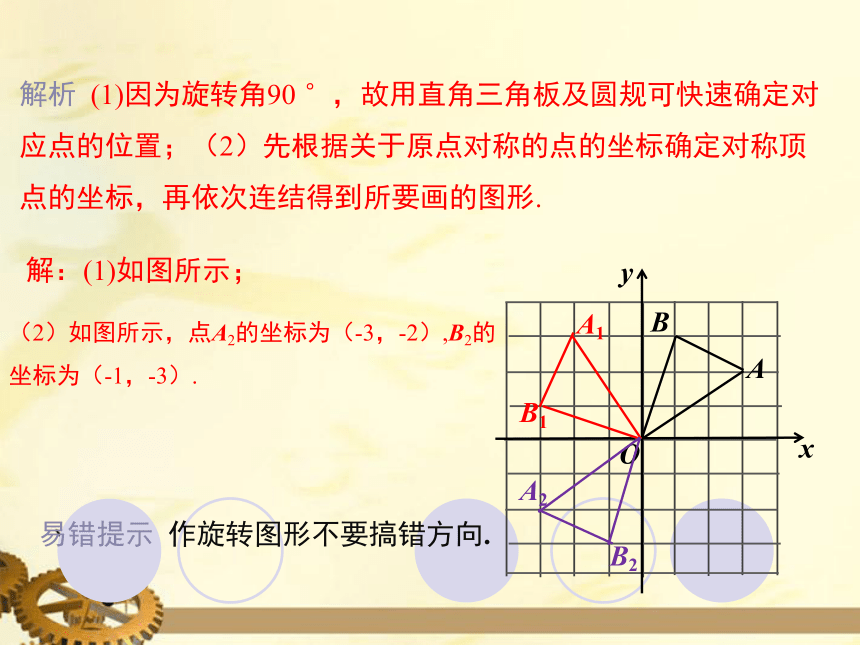
解析 (1)因为旋转角90 °,故用直角三角板及圆规可快速确定对应点的位置;(2)先根据关于原点对称的点的坐标确定对称顶点的坐标,再依次连结得到所要画的图形.
易错提示 作旋转图形不要搞错方向.
解:(1)如图所示;
(2)如图所示,点A2的坐标为(-3,-2),B2的坐标为(-1,-3).
例4 如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成面积相等的两部分,并说明理由.
A
B
C
F
E
D
解: 矩形FABE是中心对称图形,矩形 BCDE也是中心对称图形,所以经过它们中心的直线把图形分成全等的两部分,面积相等.如图直线l既经过矩形FABE的中心,又经过菱形BCDE的中心,所以它把纸片分成面积相等的两部分.
l
配套训练 如图,从前一个农民有一块平行四边形的土地,地里有一个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿子,中间池塘也平分.财主的两个儿子不知怎么做,你能想个办法吗?
解析 先找到平行四边形对角线的交点A,过点A、B两点作一条直线可以了.
A
B
专题四 平面直角坐标系中的中心对称
例5 如图,菱形ABCD的对角线交于平面直角坐标系的原点,顶点A坐标为(-2,3),现将菱形绕点O顺时针方向旋转180 ° 后,A点的坐标为 .
x
y
O
A
B
C
D
(2,-3)
解析 菱形ABCD是中心对称图形,且其对称中心又在原点,根据菱形对角线的性质,对角线交点即为对称中心,点A与点C关于原点对称,故C点的坐标为(2,-3).
配套训练 已知点A(a,1)与点B(5,b) 关于原点对称,则a= ,b= .
-5
-1
旋转
旋转的概念
在解题时如果没有指明旋转方向通常要分顺时针和逆时针两种情况讨论.
旋转的性质
①要熟练地找出可以作为旋转角的角;
②要明确旋转中心的确定方法.
中心对称及中心对称图形
①中心对称是一种特殊的旋转;
②中心对称图形与轴对称图形的区别.
课堂小结
1.如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
A. 12π B. 24π C. 6π D.36π
A
B
B ′
B
课后训练
2.(分类讨论题)如图,在Rt△ABC中, ∠C=90 °, ∠B=50°,且BD=2CD,现将△ABC绕着点D逆时针旋转m(0C
B
D
A
80°或120°
C
B
D
A
B1
B2
答题图
3.如图, ∠ABC=90 °,点P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC的内部作和等边△ABE等边△APQ,连接QE并延长BP于点F.求证:BF=EF.
A
B
Q
P
E
F
C
思路点拨
证△ABP ≌ △AEP(SAS)
∠AEQ= ∠ABP=90 °
∠EBP= ∠BEF=30 °
BF=EF
4.如图a,点A是线段BC上一点, △ABD和△ACE都是等边三角形.(1)连接BE,CD,求证:BE=DC;
(2)在图②中,将△ABD绕点A顺时针旋转到△AB′D′.
①当旋转角为 度时,边AD恰好落在AE边上;
②在①的条件下,延长DD′交CE于点P,连接BD ′,CD ′.当线段AB,AC满足什么数量关系时, △BDD ′与△CPD ′全等?并给予证明.
A
B
C
D
E
图a
A
B
C
D
E
图b
D ′
(B′)
P
A
B
C
D
E
图a
A
B
C
D
E
图b
D ′
(B′)
P
(2) ①60 °;
②满足AC=2AB时, △BDD ′与△CPD ′全等;
证明如下:由旋转可知等边△ABD ≌
等边△AB′D′,
∴AB=AD ′=DD ′ =BD=AD,
∴四边形AD ′DB是菱形 .
∴D ′P ∥AC,
又∵ AC=2AB,
∴AE=2AD ′ ,
∴D ′ P是△ACE的中位线;
∴D ′P= AC,PC= EC,
∵ △ABD和△ACE都是等边三角形,
且B、A、C三点共线,
∴ ∠BDD ′ = ∠ D ′ PC=120 °,
又知D ′ P =PC=BD ′ =DD ′,
∴ △BDD ′ ≌ △CPD ′(SAS).
第二十三章 旋 转
复习课
旋转的概念
旋转中心
旋转方向
旋转角度
旋转的三要素
基本
性质
①旋转前后的图形全等
②对应点到旋转中心的距离相等
旋 转
图形的旋转
③对应点与旋转中心所连线段的夹角等于旋转角
旋转
作图
定
找
旋
连
中心对称
中心对称
定义
旋转180 °
性质
对称中心是对称点连线段的中点(即两个对称点与对称中心三点共线
中心对称图形
性质
经过对称中心的直线把原图形面积平分
专题一 旋转的概念及性质的应用
例1 (1)如图a,将△AOB绕点O按逆时针方
向旋转60 °后得到△COD,若∠AOB=15 °,
则∠AOD的度数是( )
A. 15 ° B. 60 ° C. 45 ° D. 75 °
(2) 如图b ,4 ×4的正方形网格中, △MNP绕某
点旋转一定的角度,得到△M1N1P1,其旋转中
心是( )
A. 点A B. 点B C. 点C D. 点D
A
B
O
D
C
图a
C
N1
M1
N
M
P1
D
P
A
B
图b
C
B
思路点拨 (1)关键找出旋转角∠BOD=60 °;
(2)作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
配套训练 如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 .
A
B
C
D
E
O
4
方法指导 中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
配套训练 下列说法不正确的是( )
A.任何一个具有对称中心的四边形都是平行四边形
B.平行四边形既是轴对称图形,又是中心对称图形
C.线段、平行四边形、矩形、菱形、正方形都是中心对称图形
D.正三角形、矩形、菱形、正方形都是轴对称图形,且对称轴都不止一条.
B
专题三 与旋转有关的作图
例3 如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△AOB的顶点均在格点上,建立如图所示的平面直角坐标系,点A、B的坐标分别是A(3,2) 、B(1,3).
x
y
O
A
B
(1)将△AOB绕点O逆时针旋转90 °后得到△A1OB1,画出旋转后的图形;
(2)画出△AOB关于原点O对称的图形△A2OB2,并写出点A2,B2的坐标.
x
y
O
A
B
A1
B1
A2
B2
解析 (1)因为旋转角90 °,故用直角三角板及圆规可快速确定对应点的位置;(2)先根据关于原点对称的点的坐标确定对称顶点的坐标,再依次连结得到所要画的图形.
易错提示 作旋转图形不要搞错方向.
解:(1)如图所示;
(2)如图所示,点A2的坐标为(-3,-2),B2的坐标为(-1,-3).
例4 如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成面积相等的两部分,并说明理由.
A
B
C
F
E
D
解: 矩形FABE是中心对称图形,矩形 BCDE也是中心对称图形,所以经过它们中心的直线把图形分成全等的两部分,面积相等.如图直线l既经过矩形FABE的中心,又经过菱形BCDE的中心,所以它把纸片分成面积相等的两部分.
l
配套训练 如图,从前一个农民有一块平行四边形的土地,地里有一个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿子,中间池塘也平分.财主的两个儿子不知怎么做,你能想个办法吗?
解析 先找到平行四边形对角线的交点A,过点A、B两点作一条直线可以了.
A
B
专题四 平面直角坐标系中的中心对称
例5 如图,菱形ABCD的对角线交于平面直角坐标系的原点,顶点A坐标为(-2,3),现将菱形绕点O顺时针方向旋转180 ° 后,A点的坐标为 .
x
y
O
A
B
C
D
(2,-3)
解析 菱形ABCD是中心对称图形,且其对称中心又在原点,根据菱形对角线的性质,对角线交点即为对称中心,点A与点C关于原点对称,故C点的坐标为(2,-3).
配套训练 已知点A(a,1)与点B(5,b) 关于原点对称,则a= ,b= .
-5
-1
旋转
旋转的概念
在解题时如果没有指明旋转方向通常要分顺时针和逆时针两种情况讨论.
旋转的性质
①要熟练地找出可以作为旋转角的角;
②要明确旋转中心的确定方法.
中心对称及中心对称图形
①中心对称是一种特殊的旋转;
②中心对称图形与轴对称图形的区别.
课堂小结
1.如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
A. 12π B. 24π C. 6π D.36π
A
B
B ′
B
课后训练
2.(分类讨论题)如图,在Rt△ABC中, ∠C=90 °, ∠B=50°,且BD=2CD,现将△ABC绕着点D逆时针旋转m(0
B
D
A
80°或120°
C
B
D
A
B1
B2
答题图
3.如图, ∠ABC=90 °,点P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC的内部作和等边△ABE等边△APQ,连接QE并延长BP于点F.求证:BF=EF.
A
B
Q
P
E
F
C
思路点拨
证△ABP ≌ △AEP(SAS)
∠AEQ= ∠ABP=90 °
∠EBP= ∠BEF=30 °
BF=EF
4.如图a,点A是线段BC上一点, △ABD和△ACE都是等边三角形.(1)连接BE,CD,求证:BE=DC;
(2)在图②中,将△ABD绕点A顺时针旋转到△AB′D′.
①当旋转角为 度时,边AD恰好落在AE边上;
②在①的条件下,延长DD′交CE于点P,连接BD ′,CD ′.当线段AB,AC满足什么数量关系时, △BDD ′与△CPD ′全等?并给予证明.
A
B
C
D
E
图a
A
B
C
D
E
图b
D ′
(B′)
P
A
B
C
D
E
图a
A
B
C
D
E
图b
D ′
(B′)
P
(2) ①60 °;
②满足AC=2AB时, △BDD ′与△CPD ′全等;
证明如下:由旋转可知等边△ABD ≌
等边△AB′D′,
∴AB=AD ′=DD ′ =BD=AD,
∴四边形AD ′DB是菱形 .
∴D ′P ∥AC,
又∵ AC=2AB,
∴AE=2AD ′ ,
∴D ′ P是△ACE的中位线;
∴D ′P= AC,PC= EC,
∵ △ABD和△ACE都是等边三角形,
且B、A、C三点共线,
∴ ∠BDD ′ = ∠ D ′ PC=120 °,
又知D ′ P =PC=BD ′ =DD ′,
∴ △BDD ′ ≌ △CPD ′(SAS).
同课章节目录
