人教版八年级数学上册 第十三章轴对称 13.1.2线段的垂直平分线的性质 课后练习(word版含答案)
文档属性
| 名称 | 人教版八年级数学上册 第十三章轴对称 13.1.2线段的垂直平分线的性质 课后练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 286.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 00:10:46 | ||
图片预览




文档简介
人教版八年级数学上册
第十三章轴对称
13.1.2线段的垂直平分线的性质
课后练习
一、单选题
1.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
2.如图所示,D是线段AB,BC垂直平分线的交点,若,则的大小是(
).
A.
B.
C.
D.
3.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为(
)
A.1cm
B.2cm
C.3cm
D.4cm
4.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C为( )
A.24°
B.30°
C.21°
D.40°
5.如图,在中,,平分交于点,垂直平分交于点.若,则等于(
).
A.
B.
C.
D.
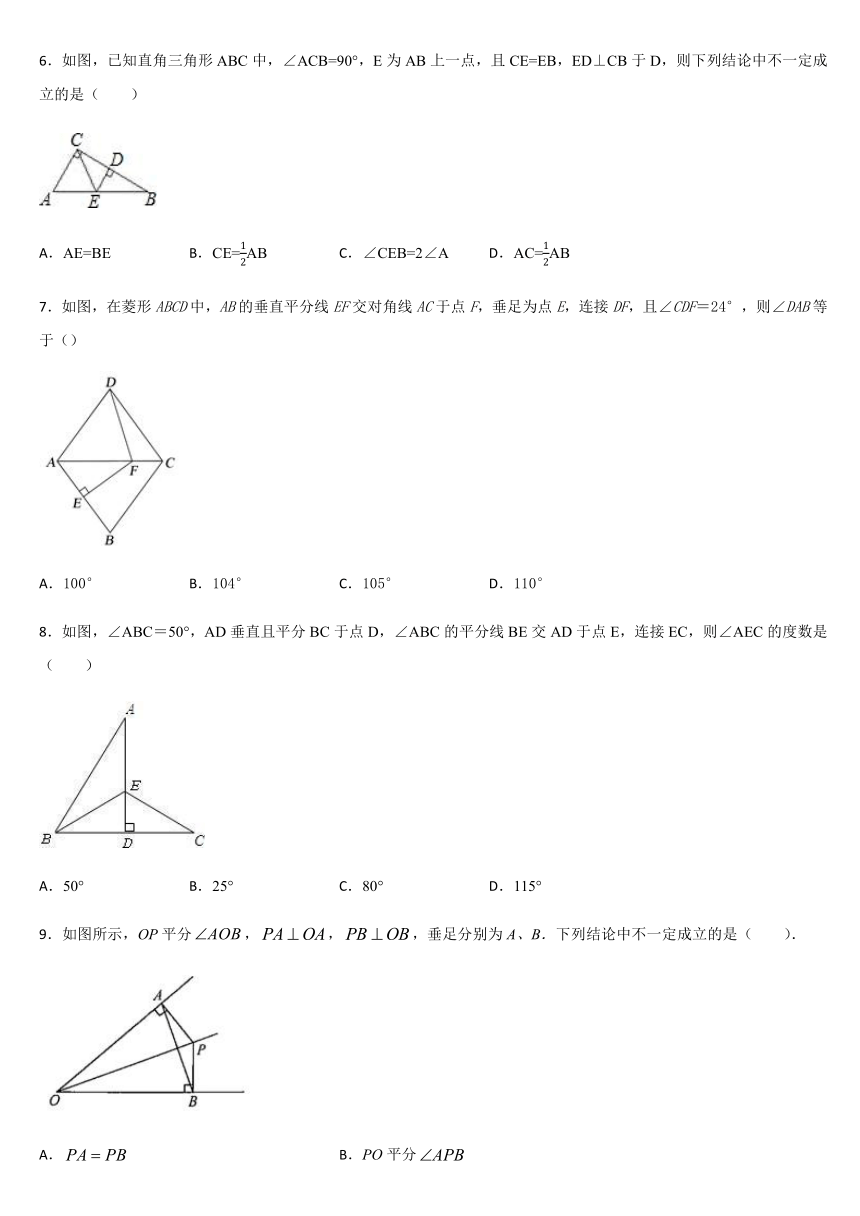
6.如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
A.AE=BE
B.CE=AB
C.∠CEB=2∠A
D.AC=AB
7.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=24°,则∠DAB等于()
A.100°
B.104°
C.105°
D.110°
8.如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是(
)
A.50°
B.25°
C.80°
D.115°
9.如图所示,OP平分,,,垂足分别为A、B.下列结论中不一定成立的是(
).
A.
B.PO平分
C.
D.AB垂直平分OP
10.如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E,若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
A.12
B.6
C.24
D.36
二、填空题
11.平面上的两条相交直线是轴对称图形,它有______条对称轴.
12.如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为___________________.
13.底边为定长的等腰三角形的顶点的轨迹是______.
14.以线段为底边的等腰三角形顶点的轨迹是______.
15.和已知线段的两端点距离相等,且到一个已知点的距离等于定长的点最多有______个.
三、解答题
16.如图所示,在中,AD是平分线,AD的垂直平分线分别交AB、BC延长线于点F、E.
求证:(1);
(2);
(3).
17.如图,在△ABC中,AB=AC,AD平分∠CAB,N点是AB上的一定点,M是AD上一动点,要使MB+MN最小,请找点M的位置.
18.如图,已知,在内部的点到两边的距离相等,且.
(1)利用尺规作图,确定符合条件的点(保留作图痕迹,不必写出做法);
(2)过点作的垂线,垂足在延长线上,求证:;
(3)当时,判断的形状,并证明你的结论;
19.(1)已知和线段、,用直尺和圆规作,使,,和之间的距离为(作出图形,不写作法,保留痕迹)
(2)在(1)中,若比大2,且与的和小于10,求的取值范围.
20.如图,中,,,AD平分交OB于D,交AB于E,垂足为F.
(1)求证:;?
(2)若,求的值.
21.如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短?若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=52°,在(1)的条件下,求出∠MPN的度数.
22.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
23.已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
【参考答案】
1.D
2.A
3.C
4.A
5.D
6.D
7.B
8.D
9.D
10.B
11.2
12.(-2,-1)
13.底边的垂直平分线(底边的中点除外)
14.线段的垂直平分线(线段的中点除外)
15.2
16.(1)是AD的垂直平分线,
,.
(2)是AD的垂直平分线,
,
,
是平分线,
,
,.
(3),,
且,,
.
17.如图,连接NC与AD的交点为M点.点M即为所求.
18.(1)如图所示,P点即为所求;
(2)作于,联结、.
点在的平分线上,
.
在和中,
.
.
,,
.
又∵,
.
(3),
.
在中,,
同理
由(2)知,
.
,即.
又,
是等腰直角三角形.
19.解:(1)如图,平行四边形为所作.
(2)根据题意得到m=n+2,m+n<10,则2n+2<10,
解得n<4,
而n>0,
所以0<n<4.
20.(1)证明:连接DE,
∵OE⊥AD,
∴∠AFE=∠AFO=90°,
∵AD平分∠EAO,
∴∠EAF=∠OAF,
在△EAF和△OAF中
,
∴△EAF≌△OAF(ASA),
∴AE=AO,∠AEO=∠AOE,
∵AD⊥OE,
∴EF=FO,
∴DE=DO,
∴∠DEO=∠DOE,
∵∠AEO=∠AOE,
∴∠AED=∠AOB=90°,
∵∠AOB=90°,AO=BO,
∴∠B=45°,
∴∠EDB=∠AEO-∠B=90°-45°=45°=∠B,
∴BE=DE,
∴OD=BE;
(2)解:在AD上截AM=OE,连接OM,
∵∠OAB=∠B=45°,AD平分∠OAB,
∴∠OAM=22.5°,
∵OD=DE,
∴∠DEO=∠DOE,
∵∠EDB=45°=∠DEO+∠DOE,
∴∠EOB=22.5°=∠OAM,
在△AMO和△OEB中,
,
∴△AMO≌△OEB(SAS),
∴MO=BE=OD,
∵OE⊥AD,
∴DF=MF,
?∴AD-OE=DM=2DF=2.
21.(1)①作出点P关于AC、BC的对称点D、G.
②连接DG交AC、BC于点M、N.点M、N即为所求.
(2)设PD交AC于E,PG交BC于F,
∵PD⊥AC,PG⊥BC,∴∠PEC=∠PFC=90°,∴∠C+∠EPF=180°.
∵∠C=52°,∴∠EPF=128°.
∵∠D+∠G+∠EPF=180°,∴∠D+∠G=52°.
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=52°,∴∠MPN=128°-52°=76°.
22.作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.
∵∠DAB=120°,∴∠HAA′=60°.∴∠AA′M+∠A″=∠HAA′=60°.
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.
23.(1)图略,点A,B即为所求.画法:①作点M关于射线OP的对称点M′;②连接M′N交OP于点A;③作点N关于射线OQ的对称点N′;④连接N′M交OQ于点B.
(2)AM+AN=BM+BN.
第十三章轴对称
13.1.2线段的垂直平分线的性质
课后练习
一、单选题
1.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
2.如图所示,D是线段AB,BC垂直平分线的交点,若,则的大小是(
).
A.
B.
C.
D.
3.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为(
)
A.1cm
B.2cm
C.3cm
D.4cm
4.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C为( )
A.24°
B.30°
C.21°
D.40°
5.如图,在中,,平分交于点,垂直平分交于点.若,则等于(
).
A.
B.
C.
D.
6.如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
A.AE=BE
B.CE=AB
C.∠CEB=2∠A
D.AC=AB
7.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=24°,则∠DAB等于()
A.100°
B.104°
C.105°
D.110°
8.如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是(
)
A.50°
B.25°
C.80°
D.115°
9.如图所示,OP平分,,,垂足分别为A、B.下列结论中不一定成立的是(
).
A.
B.PO平分
C.
D.AB垂直平分OP
10.如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E,若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
A.12
B.6
C.24
D.36
二、填空题
11.平面上的两条相交直线是轴对称图形,它有______条对称轴.
12.如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为___________________.
13.底边为定长的等腰三角形的顶点的轨迹是______.
14.以线段为底边的等腰三角形顶点的轨迹是______.
15.和已知线段的两端点距离相等,且到一个已知点的距离等于定长的点最多有______个.
三、解答题
16.如图所示,在中,AD是平分线,AD的垂直平分线分别交AB、BC延长线于点F、E.
求证:(1);
(2);
(3).
17.如图,在△ABC中,AB=AC,AD平分∠CAB,N点是AB上的一定点,M是AD上一动点,要使MB+MN最小,请找点M的位置.
18.如图,已知,在内部的点到两边的距离相等,且.
(1)利用尺规作图,确定符合条件的点(保留作图痕迹,不必写出做法);
(2)过点作的垂线,垂足在延长线上,求证:;
(3)当时,判断的形状,并证明你的结论;
19.(1)已知和线段、,用直尺和圆规作,使,,和之间的距离为(作出图形,不写作法,保留痕迹)
(2)在(1)中,若比大2,且与的和小于10,求的取值范围.
20.如图,中,,,AD平分交OB于D,交AB于E,垂足为F.
(1)求证:;?
(2)若,求的值.
21.如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短?若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=52°,在(1)的条件下,求出∠MPN的度数.
22.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
23.已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
【参考答案】
1.D
2.A
3.C
4.A
5.D
6.D
7.B
8.D
9.D
10.B
11.2
12.(-2,-1)
13.底边的垂直平分线(底边的中点除外)
14.线段的垂直平分线(线段的中点除外)
15.2
16.(1)是AD的垂直平分线,
,.
(2)是AD的垂直平分线,
,
,
是平分线,
,
,.
(3),,
且,,
.
17.如图,连接NC与AD的交点为M点.点M即为所求.
18.(1)如图所示,P点即为所求;
(2)作于,联结、.
点在的平分线上,
.
在和中,
.
.
,,
.
又∵,
.
(3),
.
在中,,
同理
由(2)知,
.
,即.
又,
是等腰直角三角形.
19.解:(1)如图,平行四边形为所作.
(2)根据题意得到m=n+2,m+n<10,则2n+2<10,
解得n<4,
而n>0,
所以0<n<4.
20.(1)证明:连接DE,
∵OE⊥AD,
∴∠AFE=∠AFO=90°,
∵AD平分∠EAO,
∴∠EAF=∠OAF,
在△EAF和△OAF中
,
∴△EAF≌△OAF(ASA),
∴AE=AO,∠AEO=∠AOE,
∵AD⊥OE,
∴EF=FO,
∴DE=DO,
∴∠DEO=∠DOE,
∵∠AEO=∠AOE,
∴∠AED=∠AOB=90°,
∵∠AOB=90°,AO=BO,
∴∠B=45°,
∴∠EDB=∠AEO-∠B=90°-45°=45°=∠B,
∴BE=DE,
∴OD=BE;
(2)解:在AD上截AM=OE,连接OM,
∵∠OAB=∠B=45°,AD平分∠OAB,
∴∠OAM=22.5°,
∵OD=DE,
∴∠DEO=∠DOE,
∵∠EDB=45°=∠DEO+∠DOE,
∴∠EOB=22.5°=∠OAM,
在△AMO和△OEB中,
,
∴△AMO≌△OEB(SAS),
∴MO=BE=OD,
∵OE⊥AD,
∴DF=MF,
?∴AD-OE=DM=2DF=2.
21.(1)①作出点P关于AC、BC的对称点D、G.
②连接DG交AC、BC于点M、N.点M、N即为所求.
(2)设PD交AC于E,PG交BC于F,
∵PD⊥AC,PG⊥BC,∴∠PEC=∠PFC=90°,∴∠C+∠EPF=180°.
∵∠C=52°,∴∠EPF=128°.
∵∠D+∠G+∠EPF=180°,∴∠D+∠G=52°.
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=52°,∴∠MPN=128°-52°=76°.
22.作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.
∵∠DAB=120°,∴∠HAA′=60°.∴∠AA′M+∠A″=∠HAA′=60°.
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.
23.(1)图略,点A,B即为所求.画法:①作点M关于射线OP的对称点M′;②连接M′N交OP于点A;③作点N关于射线OQ的对称点N′;④连接N′M交OQ于点B.
(2)AM+AN=BM+BN.
