人教版七年级数学上册1.3.1.2有理数加法的运算律教学课件(共27张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.3.1.2有理数加法的运算律教学课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
1.3.1.2有理数加法的运算律
第一章
有理数
人教版七年级数学上册
1.有理数加法法则要点
(1)同号两数相加,取
.
相同的符号,
并把绝对值相加
(2)绝对值不相等的异号两数相加:
取绝对值较大加数的符号,
并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同零相加仍得这个数.
新课导入
2.算一算
(1)(-10)
+
(-8)=
(2)(-6)
+
(
+
9)=
(3)(-37)
+
0=
(4)(-3.86)
+
(
+
3.86)=
(5)(+416)
+
0=
(6)(+6)
+
(
+
9)=
-18
3
-37
0
+416
15
新课导入
比一比,看谁算的快!
(1)
(2)
=
200
=
28
猜想:加法的交换律和结合律是否仍适用于有理数的加法运算?
同学们是怎么运算使计算简便的?用到了什么运算律?
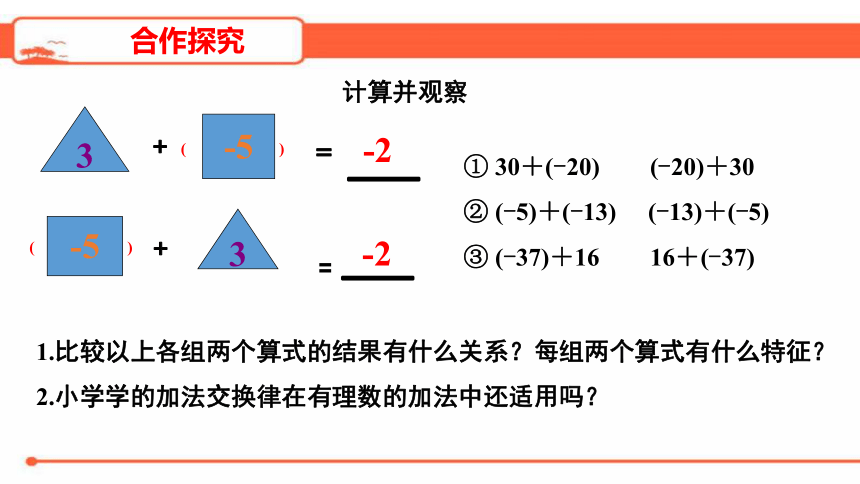
新课导入
3
-5
﹢
(
)
﹦
_
(
)
-5
﹢
3
﹦
_
-2
-2
①
30+(-20)
(-20)+30
②
(-5)+(-13)
(-13)+(-5)
③
(-37)+16
16+(-37)
1.比较以上各组两个算式的结果有什么关系?每组两个算式有什么特征?
2.小学学的加法交换律在有理数的加法中还适用吗?
计算并观察
合作探究
你能用精炼的语言表述这一结论吗?你能把该规律用字母表示吗?
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:
3+(-5)=(-5)+3
30+(-20)
=
(-20)+30
(-5)+(-13)
=(-13)+(-5)
(-37)+16
=16+(-37)
归纳总结
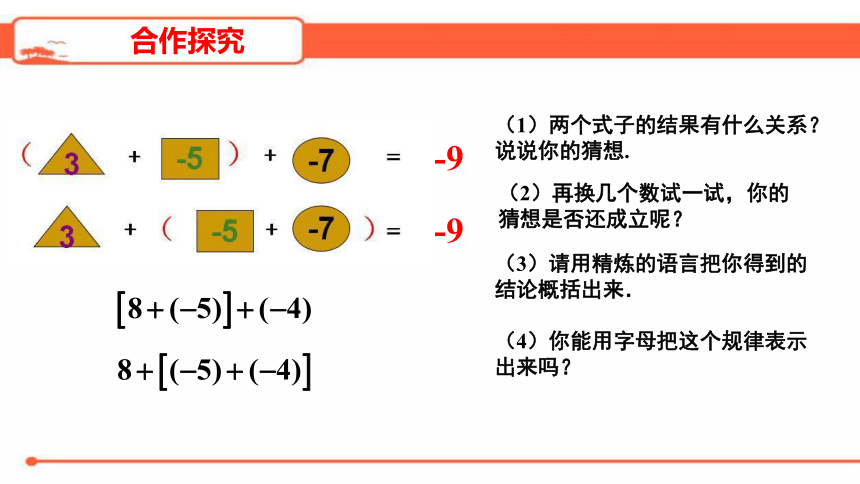
-9
-9
(1)两个式子的结果有什么关系?
说说你的猜想.
(2)再换几个数试一试,你的猜想是否还成立呢?
(3)请用精炼的语言把你得到的结论概括出来.
(4)你能用字母把这个规律表示出来吗?
合作探究
[3+(-5)]+(-7)=3+[(-5)+(-7)]
[8+(-5)]+(-4)=8+[(-5)+(-4)]
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
(a+b)+c=a+(b+c)
加法的结合律:
归纳总结
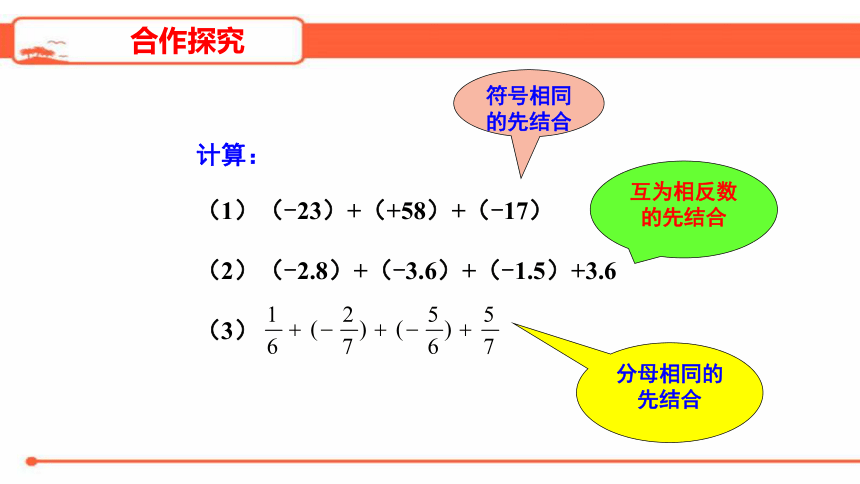
计算:
(1)(-23)+(+58)+(-17)
(2)(-2.8)+(-3.6)+(-1.5)+3.6
(3)
符号相同的先结合
互为相反数的先结合
分母相同的先结合
合作探究
运算律的应用
计算:
①
②
合理运用运算律简化计算,有哪些方法?
同分母结合相加
能“凑0”或“凑整”的结合相加
合作探究
例1
计算16
+
(-25)
+
24+
(-35).
解:
16
+
(-25)
+
24+
(-35)
=
16
+
24
+
[
(-25)
+
(-35)]
=40+
(-60)
=-20.
本例中是怎样使计算简化的?根据是什么?
例题精析
有理数的加法中,三个数相加,先把前两
个数相加,或者先把后两个数相加,和不变.
加法结合律:(a+b)+c=a+(b+c).
例题精析
例2
计算:43+(-77)+37+(-23).
导引:
先把正数、负数分别结合,然后再计算.
解:
原式=(43+37)+[(-77)+(-23)]
=80+(-100)
=-20.
例题精析
在有理数的加法运算中,先将所有的正数结
合在一起,所有的负数结合在一起,再进行运算,
简称同号结合法.
例题精析
例3
计算:
导引:将-3.75,
-2.5和2.85,3.15分
别结合在一起,然后相加.
解:原式=
例题精析
在有理数的运算中,如果既有分数又有小数,
一般先将小数转化为分数(有时也将分数转化为小
数),然后把能凑成整数的数结合在一起,这样能
使计算简便,简称凑整法.
例题精析
例4
5袋大米,以每袋50千克为标准,超过的千克数记作正数,不足的千克数记作负数,称重记录如下(单位:千克):+0.5,-0.2,0,-0.3,+0.3,则这5袋大米共超过或不足多少
千克?总质量为多少?
导引:
先利用称重记录数据求出超过或不足的千克数,再用5袋的标准总质量加上这个数,即得最后总质量.
例题精析
解:(+0.5)+(-0.2)+0+(-0.3)+(+0.3)
=[(+0.5)+(-0.2)]+0+[(-0.3)+(+0.3)]
=0.3+0+0
=0.3(千克),
50×5+0.3=250+0.3=250.3(千克).
答:这5袋大米共超过0.3千克,总质量为250.3千克.
例题精析
利用正负数表示相反意义的量,减少了大
数字计算的繁琐,注意在求总质量时,千万不
能忽视平均量的总量.
例题精析
例5
10袋小麦称后记录如图所示(单位:kg).
(1)10袋小麦一共多少千克?
(2)如果每袋小麦以90
kg为标准,10袋小麦总计超过多少千克或不足多少千克?
在计算中我们可以使用哪些运算律?
例题精析
解法1:
10袋小麦一共多少千克:91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4(千克).
再计算总计超过多少千克:
905.4-90×10=5.4(千克).
解法2:
我们以每袋小麦以90千克为标准,超过记为正,不足记为负,则10袋小麦可记为:
1,1,1.5,-1,1.2,1.3,-1.3,-1.2,1.8,1.1
它们的和为:1+1+1.5-1+1.2+1.3-1.3-1.2+1.8+1.1=5.4
.
答:10袋小麦一共90×10+5.4=905.4千克,10袋小麦总计超过5.4千克.?
例题精析
1.
在括号内填上适当的数:
(-31)
+(+19)
+(-5)
+(+31)=
[(-31)
+(
)]+[(
)
+(
)].
+31
+19
-5
2.
在算式每一步后面填上这一步所根据的运算律:
(+7)
+(-22)
+(-7)
=(-22)
+(+7)
+(-7)
____________
=(-22)
+[(+7)+(-7)]
____________
=(-22)
+0
=-22.
加法交换律
加法结合律
课堂精练
3.
计算:(-1.75)+(+7.3)+(-2.25)+(-8.5)+(+1.5)=[(-1.75)+(-2.25)]+[(+1.5)+(-8.5)]+(+7.3)运用了( )
A.加法的交换律
B.加法的结合律
C.加法的交换律和结合律
D.以上都不对
C
4.
计算(-20)+3
+20+
,比较合适的做法是( )
A.把一、三两个加数结合,二、四两个加数结合
B.把一、二两个加数结合,三、四两个加数结合
C.把一、四两个加数结合,二、三两个加数结合
D.把一、二、四这三个加数先结合
A
课堂精练
5.
计算
运用运算律计算恰当的是( )
A.
B.
C.
D.以上都不恰当
A
课堂精练
6.
检修小组从A地出发,在东西路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中行驶记录如下(单位:千米):-4,+7,-9,+8,+6,-4,-3.则收工时检修小组在A地的________边________千米.
东
1
课堂精练
1.本节课我们学习了哪些加法运算律?
有理数的加法运算律及其应用:
①先将相反数相加;
②再将其中的同号的数相加;
③最后求异号加数的和,有分数时,可把相加得
整数的先加起来.
加法交换律:
加法结合律:
a
+
b
=
b
+
a
a+(
b+
c
)=(
a
+b
)+c
课堂小结
2.我们在哪些情况下考虑使用加法运算律呢?
①互为相反数的两个数先相加——相反数结合法;
②符号相同的两个数先相加——同号结合法;
③分母相同的数先相加——同分母结合法;
④几个数相加得到整数,先相加——凑整法;
⑤整数与整数,小数与小数相加——同形结合法.
课堂小结
1.3.1.2有理数加法的运算律
第一章
有理数
人教版七年级数学上册
1.有理数加法法则要点
(1)同号两数相加,取
.
相同的符号,
并把绝对值相加
(2)绝对值不相等的异号两数相加:
取绝对值较大加数的符号,
并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同零相加仍得这个数.
新课导入
2.算一算
(1)(-10)
+
(-8)=
(2)(-6)
+
(
+
9)=
(3)(-37)
+
0=
(4)(-3.86)
+
(
+
3.86)=
(5)(+416)
+
0=
(6)(+6)
+
(
+
9)=
-18
3
-37
0
+416
15
新课导入
比一比,看谁算的快!
(1)
(2)
=
200
=
28
猜想:加法的交换律和结合律是否仍适用于有理数的加法运算?
同学们是怎么运算使计算简便的?用到了什么运算律?
新课导入
3
-5
﹢
(
)
﹦
_
(
)
-5
﹢
3
﹦
_
-2
-2
①
30+(-20)
(-20)+30
②
(-5)+(-13)
(-13)+(-5)
③
(-37)+16
16+(-37)
1.比较以上各组两个算式的结果有什么关系?每组两个算式有什么特征?
2.小学学的加法交换律在有理数的加法中还适用吗?
计算并观察
合作探究
你能用精炼的语言表述这一结论吗?你能把该规律用字母表示吗?
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:
3+(-5)=(-5)+3
30+(-20)
=
(-20)+30
(-5)+(-13)
=(-13)+(-5)
(-37)+16
=16+(-37)
归纳总结
-9
-9
(1)两个式子的结果有什么关系?
说说你的猜想.
(2)再换几个数试一试,你的猜想是否还成立呢?
(3)请用精炼的语言把你得到的结论概括出来.
(4)你能用字母把这个规律表示出来吗?
合作探究
[3+(-5)]+(-7)=3+[(-5)+(-7)]
[8+(-5)]+(-4)=8+[(-5)+(-4)]
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
(a+b)+c=a+(b+c)
加法的结合律:
归纳总结
计算:
(1)(-23)+(+58)+(-17)
(2)(-2.8)+(-3.6)+(-1.5)+3.6
(3)
符号相同的先结合
互为相反数的先结合
分母相同的先结合
合作探究
运算律的应用
计算:
①
②
合理运用运算律简化计算,有哪些方法?
同分母结合相加
能“凑0”或“凑整”的结合相加
合作探究
例1
计算16
+
(-25)
+
24+
(-35).
解:
16
+
(-25)
+
24+
(-35)
=
16
+
24
+
[
(-25)
+
(-35)]
=40+
(-60)
=-20.
本例中是怎样使计算简化的?根据是什么?
例题精析
有理数的加法中,三个数相加,先把前两
个数相加,或者先把后两个数相加,和不变.
加法结合律:(a+b)+c=a+(b+c).
例题精析
例2
计算:43+(-77)+37+(-23).
导引:
先把正数、负数分别结合,然后再计算.
解:
原式=(43+37)+[(-77)+(-23)]
=80+(-100)
=-20.
例题精析
在有理数的加法运算中,先将所有的正数结
合在一起,所有的负数结合在一起,再进行运算,
简称同号结合法.
例题精析
例3
计算:
导引:将-3.75,
-2.5和2.85,3.15分
别结合在一起,然后相加.
解:原式=
例题精析
在有理数的运算中,如果既有分数又有小数,
一般先将小数转化为分数(有时也将分数转化为小
数),然后把能凑成整数的数结合在一起,这样能
使计算简便,简称凑整法.
例题精析
例4
5袋大米,以每袋50千克为标准,超过的千克数记作正数,不足的千克数记作负数,称重记录如下(单位:千克):+0.5,-0.2,0,-0.3,+0.3,则这5袋大米共超过或不足多少
千克?总质量为多少?
导引:
先利用称重记录数据求出超过或不足的千克数,再用5袋的标准总质量加上这个数,即得最后总质量.
例题精析
解:(+0.5)+(-0.2)+0+(-0.3)+(+0.3)
=[(+0.5)+(-0.2)]+0+[(-0.3)+(+0.3)]
=0.3+0+0
=0.3(千克),
50×5+0.3=250+0.3=250.3(千克).
答:这5袋大米共超过0.3千克,总质量为250.3千克.
例题精析
利用正负数表示相反意义的量,减少了大
数字计算的繁琐,注意在求总质量时,千万不
能忽视平均量的总量.
例题精析
例5
10袋小麦称后记录如图所示(单位:kg).
(1)10袋小麦一共多少千克?
(2)如果每袋小麦以90
kg为标准,10袋小麦总计超过多少千克或不足多少千克?
在计算中我们可以使用哪些运算律?
例题精析
解法1:
10袋小麦一共多少千克:91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4(千克).
再计算总计超过多少千克:
905.4-90×10=5.4(千克).
解法2:
我们以每袋小麦以90千克为标准,超过记为正,不足记为负,则10袋小麦可记为:
1,1,1.5,-1,1.2,1.3,-1.3,-1.2,1.8,1.1
它们的和为:1+1+1.5-1+1.2+1.3-1.3-1.2+1.8+1.1=5.4
.
答:10袋小麦一共90×10+5.4=905.4千克,10袋小麦总计超过5.4千克.?
例题精析
1.
在括号内填上适当的数:
(-31)
+(+19)
+(-5)
+(+31)=
[(-31)
+(
)]+[(
)
+(
)].
+31
+19
-5
2.
在算式每一步后面填上这一步所根据的运算律:
(+7)
+(-22)
+(-7)
=(-22)
+(+7)
+(-7)
____________
=(-22)
+[(+7)+(-7)]
____________
=(-22)
+0
=-22.
加法交换律
加法结合律
课堂精练
3.
计算:(-1.75)+(+7.3)+(-2.25)+(-8.5)+(+1.5)=[(-1.75)+(-2.25)]+[(+1.5)+(-8.5)]+(+7.3)运用了( )
A.加法的交换律
B.加法的结合律
C.加法的交换律和结合律
D.以上都不对
C
4.
计算(-20)+3
+20+
,比较合适的做法是( )
A.把一、三两个加数结合,二、四两个加数结合
B.把一、二两个加数结合,三、四两个加数结合
C.把一、四两个加数结合,二、三两个加数结合
D.把一、二、四这三个加数先结合
A
课堂精练
5.
计算
运用运算律计算恰当的是( )
A.
B.
C.
D.以上都不恰当
A
课堂精练
6.
检修小组从A地出发,在东西路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中行驶记录如下(单位:千米):-4,+7,-9,+8,+6,-4,-3.则收工时检修小组在A地的________边________千米.
东
1
课堂精练
1.本节课我们学习了哪些加法运算律?
有理数的加法运算律及其应用:
①先将相反数相加;
②再将其中的同号的数相加;
③最后求异号加数的和,有分数时,可把相加得
整数的先加起来.
加法交换律:
加法结合律:
a
+
b
=
b
+
a
a+(
b+
c
)=(
a
+b
)+c
课堂小结
2.我们在哪些情况下考虑使用加法运算律呢?
①互为相反数的两个数先相加——相反数结合法;
②符号相同的两个数先相加——同号结合法;
③分母相同的数先相加——同分母结合法;
④几个数相加得到整数,先相加——凑整法;
⑤整数与整数,小数与小数相加——同形结合法.
课堂小结
