第一章 勾股定理 章末复习课件(共22张PPT)
文档属性
| 名称 | 第一章 勾股定理 章末复习课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
数学北师大版
八年级
第一章复习
【分析】 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
【易错题】【例】若一个三角形的三边长分别为3、4、x,则使此三角形是直角三角形的x的值是(
)
练习1.在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,求BP最小值是多少?
2.如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2.
∴BP2+PM2=BC2+AP2+PM2,
证明:连接BM,
∵MP⊥AB,
∴△BMP和△AMP均为直角三角形.
∴BP2+PM2=BM2,AP2+PM2=AM2.
同理可得,BC2+CM2=BM2.
∴BP2+PM2=BC2+CM2.
又∵CM=AM,
∴CM2=AM2=AP2+PM2.
∴BP2=BC2+AP2.
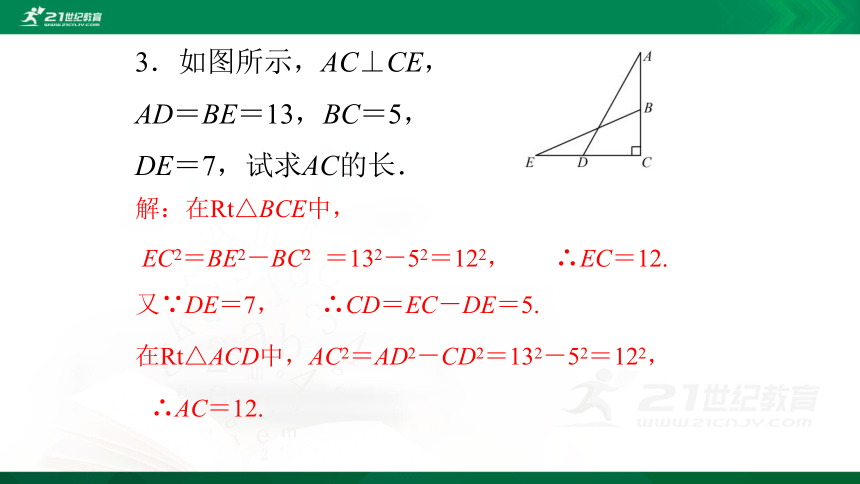
3.如图所示,AC⊥CE,AD=BE=13,BC=5,
DE=7,试求AC的长.
在Rt△ACD中,AC2=AD2-CD2=132-52=122,
解:在Rt△BCE中,
EC2=BE2-BC2
=132-52=122,
∴EC=12.
又∵DE=7,
∴CD=EC-DE=5.
∴AC=12.
4.如图,在四边形ABCD中,∠A=∠D=90°,AB=CD=24cm,AD=BC=50cm,E是AD上的一点,且AE∶ED=9∶16,试猜想∠BEC是锐角、钝角还是直角?并证明你的猜想.
解:∠BEC是直角.
证明:∵AD=50(cm),
又∵∠A=∠D=90°,由勾股定理,
AE∶ED=9∶16,
∴AE=18(cm),ED=32(cm),
又∵BE2+EC2=302+402=502=BC2.
∴∠BEC为直角.
5.如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠,使点C落在AB上的点E处,求CD的长.
即x2=(12-x)2-82,
解:在Rt△ABC中,
由勾股定理,
得AB2=AC2+BC2,
所以AB2=52+122=132,
所以AB=13.
由折叠的特性,
知CD=DE,AC=AE,∠AED=∠C=90°.
设CD=x,
则DE=x,DB=12-x,
BE=AB-AE=13-AC=13-5=8.
在Rt△BDE中,由勾股定理,
得DE2=BD2-BE2,
例2.观察右面的表格所给出的三个数a、b、c,a<b<c.
3、4、5
32+42=52
5、12、13
52+122=132
7、24、25
72+242=252
9、40、41
92+402=412
…
…
21、b、c
212+b2=c2
(1)试找出它们的共同点,并说明你的结论;
(2)当a=21时,求b、c的值.
③最小一个数的平方等于另两个数的和.即m2=n+(n+1),m为最小的数;
解:(1)共同点:
①都满足较小两个数的平方和等于大数的平方,
②最小的一个数是奇数,另外两个数是连续的正整数,
(2)b=220,c=221.
提高训练1如图,在△ABC中,D为BC的中点,AB=5,AD=6,AC=13,判断△ABD的形状.
∴∠EAB=90°,
解:延长AD至E,使DE=AD,
连接BE.
∵CD=BD,
∠ADC=∠EDB,
AD=DE,
∴△ADC≌△EDB,
∴AD=DE=6,
AC=BE=13,
在△AEB中,
AE2+AB2=
122+52
=169=BE2,
∴△ABD为直角三角形.
2.如图是一个a=5
dm,b=4
dm,c=3
dm的长方体铁盒,现在有一根长为7
dm的细铁棒(细铁棒的直径忽略不计),请问怎样才能放进这个铁盒中?请画出图形,并通过出计算说明理由.
∴这根细铁棒沿DC方向就能放进此长方体中.
解:如图可设长方体的四个顶点分别为A、B、C、D,
连结AC、DC.
在Rt△ABC和Rt△DAC中,
∠ABC=∠DAC=90°
∵a=5
dm,b=4
dm,c=3
dm,
由勾股定理可得AC2=AB2+BC2
=52+42=41
DC2=AD2+AC2=32+41=50.
∵细铁棒的长为7
dm,
且72=49<50,
∴细铁棒小于CD的长,
作业布置1.如图是一个三级台阶,它每一级的长、宽、高分别为55dm、10dm、6dm.A和B是这个台阶的两个相对的端点,A点处有一只蚂蚁,想到B点处去吃可口的食物,请你想一想,蚂蚁从A点出发,沿着台阶面爬到B点,最短路程是多少?
解:将原图中的台阶面拉平,成为如图所示的平面.
∴蚂蚁所爬的最短路程为73dm.
连接AB,
得到Rt△ACB,
AC=3×(10+6)=48(dm),
由勾股定理,得AB2=AC2+BC2
=482+552=732.
∴AB=73dm,
2.牧童在河边A处放牛,家在河边B处,时近傍晚,牧童驱赶牛群先到河边饮水,然后在天黑前赶回家.已知A点到河边的距离AC为500m,点B到河边的距离BD为700m,且CD=500m.
(1)请在原图上画出牧童回家的最短路线;
(2)求出最短路线的长度.
解:(1)作点A关于直线CD的对称点A′,连接A′B交CD于点P,点P即为所求作的点,牧童回家的最短路线为A—P—B;
根据勾股定理,得A′B2=12002+5002=13002,
(2)由作图可得最短路程为A′B的距离.
过A′作A′F⊥BD的延长线于F,
则DF=A′C=AC=500(m),
A′F=CD=500(m),
BF=700+500=1200(m).
∴A′B=1300m.即最短路线的长度为1300m.
3.要做一个如图所示的零件,按规定∠B与∠D都应为直角,已知∠B=90°,工人师傅量得所做零件的尺寸如图,这个零件符合要求吗?
所以△ACD是直角三角形,且∠D=90°.
解:连接AC.
因为在Rt△ABC中,∠B=90°,AB=24,BC=7,
所以AC2=AB2+BC2=242+72=625,
故AC=25.
因为在△ACD中,CD=15,AD=20,
所以152+202=252=AC2.
因此这个零件符合要求.
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图①).图②由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形
MNKT的面积分别为S1、s2、S3.若正方形EFGH的边长为2,则S1+S2+S3=______
5.(1)如图①,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段
AB上取点E,使∠DCE=
30°,连接AF、EF.
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
5.(1)如图①,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段
AB上取点E,使∠DCE=
30°,连接AF、EF.
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
【类比探究】(2)如图②,△ABC为等腰直角三角形,∠ACB=
90°,先将三角板的90°角与LACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=
CD,线段AB上取点E,使∠DCE=
45°,连接AF、EF.请直接写出探究结果:
①求∠EAF的度数;
②线段AE、ED、DB之间的数量关系.
①求∠EAF的度数;
②线段AE、ED、DB之间的数量关系.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
八年级
第一章复习
【分析】 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
【易错题】【例】若一个三角形的三边长分别为3、4、x,则使此三角形是直角三角形的x的值是(
)
练习1.在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,求BP最小值是多少?
2.如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2.
∴BP2+PM2=BC2+AP2+PM2,
证明:连接BM,
∵MP⊥AB,
∴△BMP和△AMP均为直角三角形.
∴BP2+PM2=BM2,AP2+PM2=AM2.
同理可得,BC2+CM2=BM2.
∴BP2+PM2=BC2+CM2.
又∵CM=AM,
∴CM2=AM2=AP2+PM2.
∴BP2=BC2+AP2.
3.如图所示,AC⊥CE,AD=BE=13,BC=5,
DE=7,试求AC的长.
在Rt△ACD中,AC2=AD2-CD2=132-52=122,
解:在Rt△BCE中,
EC2=BE2-BC2
=132-52=122,
∴EC=12.
又∵DE=7,
∴CD=EC-DE=5.
∴AC=12.
4.如图,在四边形ABCD中,∠A=∠D=90°,AB=CD=24cm,AD=BC=50cm,E是AD上的一点,且AE∶ED=9∶16,试猜想∠BEC是锐角、钝角还是直角?并证明你的猜想.
解:∠BEC是直角.
证明:∵AD=50(cm),
又∵∠A=∠D=90°,由勾股定理,
AE∶ED=9∶16,
∴AE=18(cm),ED=32(cm),
又∵BE2+EC2=302+402=502=BC2.
∴∠BEC为直角.
5.如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠,使点C落在AB上的点E处,求CD的长.
即x2=(12-x)2-82,
解:在Rt△ABC中,
由勾股定理,
得AB2=AC2+BC2,
所以AB2=52+122=132,
所以AB=13.
由折叠的特性,
知CD=DE,AC=AE,∠AED=∠C=90°.
设CD=x,
则DE=x,DB=12-x,
BE=AB-AE=13-AC=13-5=8.
在Rt△BDE中,由勾股定理,
得DE2=BD2-BE2,
例2.观察右面的表格所给出的三个数a、b、c,a<b<c.
3、4、5
32+42=52
5、12、13
52+122=132
7、24、25
72+242=252
9、40、41
92+402=412
…
…
21、b、c
212+b2=c2
(1)试找出它们的共同点,并说明你的结论;
(2)当a=21时,求b、c的值.
③最小一个数的平方等于另两个数的和.即m2=n+(n+1),m为最小的数;
解:(1)共同点:
①都满足较小两个数的平方和等于大数的平方,
②最小的一个数是奇数,另外两个数是连续的正整数,
(2)b=220,c=221.
提高训练1如图,在△ABC中,D为BC的中点,AB=5,AD=6,AC=13,判断△ABD的形状.
∴∠EAB=90°,
解:延长AD至E,使DE=AD,
连接BE.
∵CD=BD,
∠ADC=∠EDB,
AD=DE,
∴△ADC≌△EDB,
∴AD=DE=6,
AC=BE=13,
在△AEB中,
AE2+AB2=
122+52
=169=BE2,
∴△ABD为直角三角形.
2.如图是一个a=5
dm,b=4
dm,c=3
dm的长方体铁盒,现在有一根长为7
dm的细铁棒(细铁棒的直径忽略不计),请问怎样才能放进这个铁盒中?请画出图形,并通过出计算说明理由.
∴这根细铁棒沿DC方向就能放进此长方体中.
解:如图可设长方体的四个顶点分别为A、B、C、D,
连结AC、DC.
在Rt△ABC和Rt△DAC中,
∠ABC=∠DAC=90°
∵a=5
dm,b=4
dm,c=3
dm,
由勾股定理可得AC2=AB2+BC2
=52+42=41
DC2=AD2+AC2=32+41=50.
∵细铁棒的长为7
dm,
且72=49<50,
∴细铁棒小于CD的长,
作业布置1.如图是一个三级台阶,它每一级的长、宽、高分别为55dm、10dm、6dm.A和B是这个台阶的两个相对的端点,A点处有一只蚂蚁,想到B点处去吃可口的食物,请你想一想,蚂蚁从A点出发,沿着台阶面爬到B点,最短路程是多少?
解:将原图中的台阶面拉平,成为如图所示的平面.
∴蚂蚁所爬的最短路程为73dm.
连接AB,
得到Rt△ACB,
AC=3×(10+6)=48(dm),
由勾股定理,得AB2=AC2+BC2
=482+552=732.
∴AB=73dm,
2.牧童在河边A处放牛,家在河边B处,时近傍晚,牧童驱赶牛群先到河边饮水,然后在天黑前赶回家.已知A点到河边的距离AC为500m,点B到河边的距离BD为700m,且CD=500m.
(1)请在原图上画出牧童回家的最短路线;
(2)求出最短路线的长度.
解:(1)作点A关于直线CD的对称点A′,连接A′B交CD于点P,点P即为所求作的点,牧童回家的最短路线为A—P—B;
根据勾股定理,得A′B2=12002+5002=13002,
(2)由作图可得最短路程为A′B的距离.
过A′作A′F⊥BD的延长线于F,
则DF=A′C=AC=500(m),
A′F=CD=500(m),
BF=700+500=1200(m).
∴A′B=1300m.即最短路线的长度为1300m.
3.要做一个如图所示的零件,按规定∠B与∠D都应为直角,已知∠B=90°,工人师傅量得所做零件的尺寸如图,这个零件符合要求吗?
所以△ACD是直角三角形,且∠D=90°.
解:连接AC.
因为在Rt△ABC中,∠B=90°,AB=24,BC=7,
所以AC2=AB2+BC2=242+72=625,
故AC=25.
因为在△ACD中,CD=15,AD=20,
所以152+202=252=AC2.
因此这个零件符合要求.
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图①).图②由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形
MNKT的面积分别为S1、s2、S3.若正方形EFGH的边长为2,则S1+S2+S3=______
5.(1)如图①,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段
AB上取点E,使∠DCE=
30°,连接AF、EF.
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
5.(1)如图①,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段
AB上取点E,使∠DCE=
30°,连接AF、EF.
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
【类比探究】(2)如图②,△ABC为等腰直角三角形,∠ACB=
90°,先将三角板的90°角与LACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=
CD,线段AB上取点E,使∠DCE=
45°,连接AF、EF.请直接写出探究结果:
①求∠EAF的度数;
②线段AE、ED、DB之间的数量关系.
①求∠EAF的度数;
②线段AE、ED、DB之间的数量关系.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
