4.3.2 一次函数的图象(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 4.3.2 一次函数的图象(知识清单+经典例题+夯实基础+提优特训+中考链接) |
|
|
| 格式 | zip | ||
| 文件大小 | 926.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 00:00:00 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章一次函数
4.3
一次函数的图象
第2课时
一次函数的图象(2)
【知识清单】
1、一次函数的图像:
所有一次函数的图象都是一条直线;
画一次函数y=kx+b(k、b为常数,
k≠0)的图象时,只要描出点(0,b)和(,0)即可.
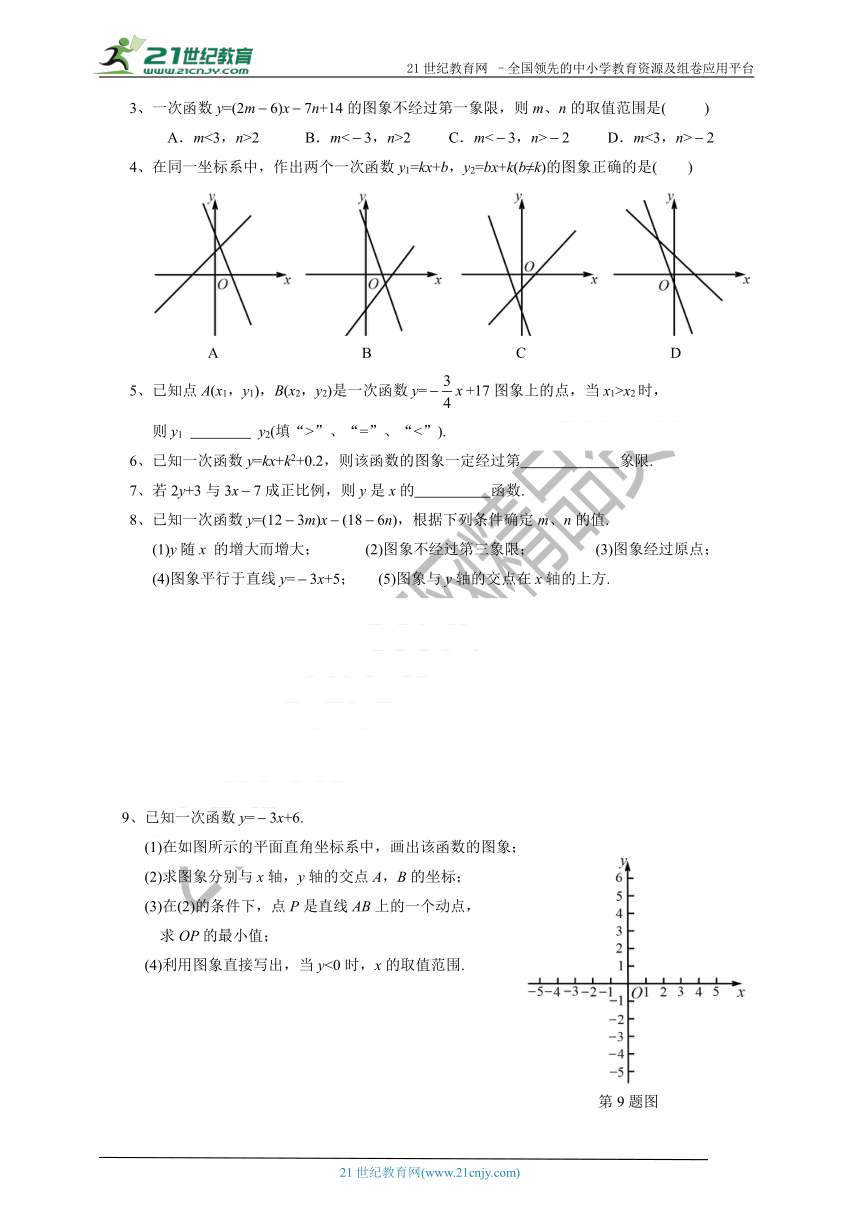
2、一次函数y=kx+b的性质:
k的符号
b的符号
函数图像
经过的象限
不经过的象限
性质
k>0
b>0
图像经过一、二、三象限.
第四象限
y随x的增大而增大.
b<0
图像经过一、三、四象限.
第二象限
k
<0
b>0
图像经过一、二、四象限.
第三象限
y随x的增大而减小.
b<0
图像经过二、三、四象限.
第一象限
3、直线y=k1x+b1与y=k2x+b2位置关系:
(1)k1=k2
,b1=b2两条直线重合;
(2)k1=k2
,b1≠b2两条直线平行;
(3)k1≠k2
,b1≠b2两条直线相交;
(4)k1≠k2
,b1=b2两条直线相交与y轴上的点(0,b).
【经典例题】
【例题】1、一条直线y=kx+b,其中k+b=3,kb=1,那么该直线经过第______象限.
【考点】一次函数图象与系数的关系.
【分析】首先根据k+b=3,kb=1确定k、b的符号,再根据图象与系数的关系确定直线经过的象限即可.
【解答】∵k+b=3,kb=1,
∴k<0,b<0
∴直线y=kx+b经过二、三、四象限,
故答案为:二、三、四.
【点评】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b<0时,直线与y轴负半轴相交.
【例题】2、已知一次函数:①y=0.3x+1;②y=
(34x)+(x5);③y=15x;④y=2x+5;
⑤y=(2x3)3(2x1);⑥y=7(3x),其中,y的值随x的增大而增大的函数是
;
y的值随x的增大而减小的函数是
;图象经过原点的函数是
.
【考点】一次函数的性质.
【分析】根据k>0,y随x的增大而增大,找出满足此条件的函数填入第一空;根据k<0,y随x的增大而减小,找出满足此条件的函数填入第二空;当b=0,图象过坐标原点,找出满足此条件的函数填入第三空.
【解答】①,③,⑥三个函数的一次项系数都大于0,所以它们的y的值都随x的增大而增大;②,④,⑤三个函数的一次项系数都小于0,所以它们的y的值都随x的增大而减小;
③,⑤为正比例函数,它们的图象都过原点.
故答案为:①,③,⑥;②,④,⑤;③,⑤.
【点评】本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.一次函数的图象是一条直线,当k>0,
y随x的增大而增大;当k<0,图象经过第二,四象限,y随x的增大而减小;当b=0,图象过坐标原点.
【夯实基础】
1、一次函数y=mx+n的图象如图所示,下列结论正确的是
( )
A.m=3,n=2
B.m=3,n=2
C.m=2,n=3
D.m=3,n=2
2、已知一次函数y=ax+b的图象如图所示,化简的结果为(
)
A.2ab
B.2a+b
C.b
D.b
3、一次函数y=(2m6)x7n+14的图象不经过第一象限,则m、n的取值范围是(
)
A.m<3,n>2
B.m<3,n>2
C.m<3,n>2
D.m<3,n>2
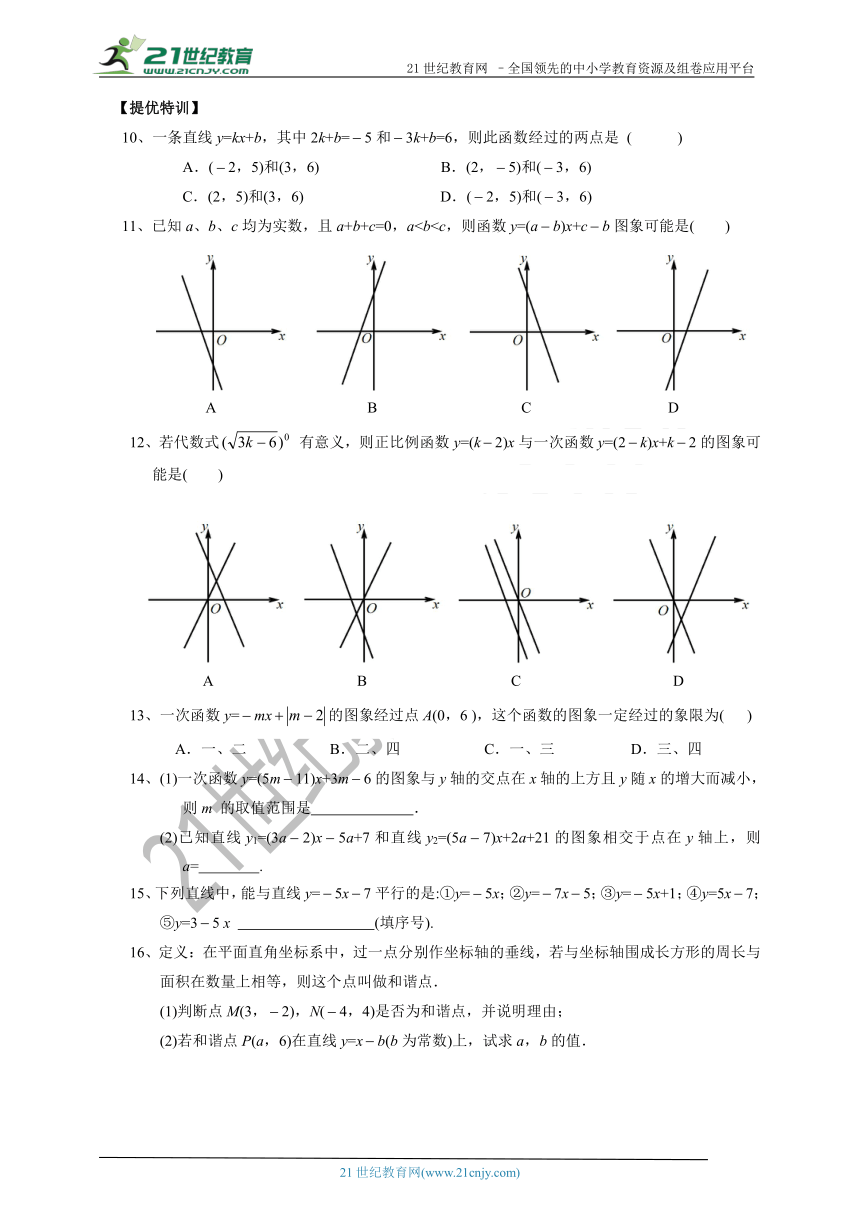
4、在同一坐标系中,作出两个一次函数y1=kx+b,y2=bx+k(b≠k)的图象正确的是( )
5、已知点A(x1,y1),B(x2,y2)是一次函数y=+17图象上的点,当x1>x2时,
则y1
y2(填“>”、“=”、“<”).
6、已知一次函数y=kx+k2+0.2,则该函数的图象一定经过第
象限.
7、若2y+3与3x7成正比例,则y是x的
函数.
8、已知一次函数y=(123m)x(186n),根据下列条件确定m、n的值.
(1)y随x
的增大而增大;
(2)图象不经过第三象限;
(3)图象经过原点;
(4)图象平行于直线y=3x+5;
(5)图象与y轴的交点在x轴的上方.
9、已知一次函数y=3x+6.
(1)在如图所示的平面直角坐标系中,画出该函数的图象;
(2)求图象分别与x轴,y轴的交点A,B的坐标;
(3)在(2)的条件下,点P是直线AB上的一个动点,
求OP的最小值;
(4)利用图象直接写出,当y<0时,x的取值范围.
【提优特训】
10、一条直线y=kx+b,其中2k+b=5和3k+b=6,则此函数经过的两点是
(
)
A.(2,5)和(3,6)
B.(2,5)和(3,6)
C.(2,5)和(3,6)
D.(2,5)和(3,6)
11、已知a、b、c均为实数,且a+b+c=0,a12、若代数式
有意义,则正比例函数y=(k2)x与一次函数y=(2k)x+k2的图象可能是( )
13、一次函数y=mx的图象经过点A(0,6
),这个函数的图象一定经过的象限为(
)
A.一、二
B.二、四
C.一、三
D.三、四
14、(1)一次函数y=(5m11)x+3m6的图象与y轴的交点在x轴的上方且y随x的增大而减小,则m
的取值范围是???
.
(2)已知直线y1=(3a2)x5a+7和直线y2=(5a7)x+2a+21的图象相交于点在y轴上,则a=
.
15、下列直线中,能与直线y=5x7平行的是:①y=5x;②y=7x5;③y=5x+1;④y=5x7;
⑤y=35
x
(填序号).
16、定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成长方形的周长与面积在数量上相等,则这个点叫做和谐点.
(1)判断点M(3,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,6)在直线y=xb(b为常数)上,试求a,b的值.
???
?
?
17、已知,如图A点的坐标为(,0),B点坐标为(0,2).
(1)求直线AB的直线解析式;
(2)过B点作直线BP与x轴交于点P,
若S△ABP=2S△AOB,求点P的坐标.
18、已知直线y1=和y2=的图象交于点A(8,7),且分别与y轴相交于B、C两点.
(1)画出符合题意的图形;
(2)求这两条直线的解析式;
(3)求△ABC的周长和面积.
【中考链接】
19、(2019?毕节)已知一次函数y=kx+b(k、b为常数,k≠0)的图象经过一、三、四象限,则下列结论正确的是(
)
A.kb>0
B.kb<0
C.k+b>0
D.k+b<0
20、(2019?扬州)若点P在一次函数y=x+4的图像上,则点P一定不在第( )象限.
A.第一象限
B.第二象限
C.第三象限
D.第四象限
21、(2019?杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )
22、(2019?成都)已知一次函数y=(k3)x+1的图象经过第一、二、四象限,则k的取值范围是
.
参考答案
1、D
2、D
3、A
4、B
5、<
6、一、二
7、一次
10、B
11、C
12、A
13、B
14、(1)
(2)
2
15、①③⑤
19、A
20、C
21、A
22、k<3
8、已知一次函数y=(123m)x(186n),根据下列条件确定m、n的值.
(1)y随x
的增大而增大;
(2)图象不经过第三象限;
(3)图象经过原点;
(4)图象平行于直线y=3x+5;
(5)图象与y轴的交点在x轴的上方.
解:(1)y随x的增大而增大,
则(123m)>0,b为任意实数;
∴m<4,b为任意实数;
(2)图象不经过第三象限,
(123m)<0且6b18>0;
∴m>4,且b>3;
(3)图象经过原点,
(123m)≠0且6b18=0,
∴m≠4,b=3;
(4)图象平行于直线y=3x+5
,
(123m)=3且6b18≠5;
∴m=5,b≠;
(5)图象与y轴的交点在x轴的上方.
则有两种情况:
①(123m)>0,6b18>0;
∴m<4,b>3,
②(123m)<0,6b18>0.
∴m>4,b>3.
9、已知一次函数y=3x+6.
(1)在如图所示的平面直角坐标系中,画出该函数的图象;
(2)求图象分别与x轴,y轴的交点A,B的坐标;
(3)在(2)的条件下,点P是直线AB上的一个动点,
求OP的最小值;
(4)利用图象直接写出,当y<0时,x的取值范围.
解:(1)令x=0,y=6;x=2,y=0,
∴一次函数y=3x+6经过A(2,0),B(0,6)两个特殊点,
∴该函数的图象如图所示:
(2)由(1)得图象分别与x轴,y轴的
交点A,B的坐标为(2,0),(0,6);
(3)当OP⊥AB时,OP的值最小,
在Rt△AOB中,OB=6,OA=2,
∴AB=,
∵S△AOB=,
∴
即2×6=×OP
OP=;
(4)由图象可得,当y<0时,x的取值范围是x>2.
16、定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成长方形的周长与面积在数量上相等,则这个点叫做和谐点.
(1)判断点M(3,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,6)在直线y=xb(b为常数)上,试求a,b的值.
解:(1)∵长方形的周长=2×(3+2)=10,
长方形的面积=3×2=6?,
长方形的周长≠长方形的面积,
???????
∴点M不是和谐点;
????????
∵长方形的周长=2×(4+4)=16,
长方形的面积=4×4=16?,
长方形的周长=长方形的面积,
???????
∴点N是和谐点.
(2)由题意:
???
?
?
2(+6)=6
???
??
解得:a=±3?,
????????
a=3时,将P
(3,6)代入得b=3
???????
?a=3时,将P
(3,6)代入得b=9.
17、已知,如图A点的坐标为(,0),B点坐标为(0,2).
(1)求直线AB的直线解析式;
(2)过B点作直线BP与x轴交于点P,
若S△ABP=2S△AOB,求点P的坐标.
解:设经过A,B两点的直线解析式
为y=kx+b(a、b为常数,a≠0),
根据题意,得0=k+b,2=b,
解得,k=,b=2,
∴过A,B两点的直线解析式为y=x2;
(2)设P点坐标为(x,0),
∵S△ABP=2S△AOB,依据图形得×2×()=2××2×,
解得,x=±2.5,
∴P点坐标分别为P1(2.5,0),P2(5,0).
18、已知直线y1=和y2=的图象交于点A(8,7),且分别与y轴相交于B、C两点.
(1)画出符合题意的图形;
(2)求这两条直线的解析式;
(3)求△ABC的周长和面积.
解:(1)将点A(8,7)代入y1=和
y2=中,得
7=,7=
解得m=22,n=1,
∴这两条直线的解析式为:y1=和y2=;
(2)过点A作AD垂直x轴于点D,作AE垂直y轴于点E,
∵A点的坐标为(8,7),
∴AD=OE=7,AE=OD=8,
令x=0,则y1=22,y2=1,
∴OB=22,OC=1∴CE=OEOC=71=6,∴BC=OBOC=221=21,
∴EB=OBOE=227=15.
在Rt△AEC中,AC=,
在Rt△AEB中,AB=,
∴△ABC的周长为AB+BC+CA=17+21+10=48;
△ABC的面积为
第9题图
第2题图
A
B
C
D
A
B
C
D
第17题图
A
B
C
D
第18题图
第17题图
第9题图
A
B
C
D
第9题图
第1题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章一次函数
4.3
一次函数的图象
第2课时
一次函数的图象(2)
【知识清单】
1、一次函数的图像:
所有一次函数的图象都是一条直线;
画一次函数y=kx+b(k、b为常数,
k≠0)的图象时,只要描出点(0,b)和(,0)即可.
2、一次函数y=kx+b的性质:
k的符号
b的符号
函数图像
经过的象限
不经过的象限
性质
k>0
b>0
图像经过一、二、三象限.
第四象限
y随x的增大而增大.
b<0
图像经过一、三、四象限.
第二象限
k
<0
b>0
图像经过一、二、四象限.
第三象限
y随x的增大而减小.
b<0
图像经过二、三、四象限.
第一象限
3、直线y=k1x+b1与y=k2x+b2位置关系:
(1)k1=k2
,b1=b2两条直线重合;
(2)k1=k2
,b1≠b2两条直线平行;
(3)k1≠k2
,b1≠b2两条直线相交;
(4)k1≠k2
,b1=b2两条直线相交与y轴上的点(0,b).
【经典例题】
【例题】1、一条直线y=kx+b,其中k+b=3,kb=1,那么该直线经过第______象限.
【考点】一次函数图象与系数的关系.
【分析】首先根据k+b=3,kb=1确定k、b的符号,再根据图象与系数的关系确定直线经过的象限即可.
【解答】∵k+b=3,kb=1,
∴k<0,b<0
∴直线y=kx+b经过二、三、四象限,
故答案为:二、三、四.
【点评】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b<0时,直线与y轴负半轴相交.
【例题】2、已知一次函数:①y=0.3x+1;②y=
(34x)+(x5);③y=15x;④y=2x+5;
⑤y=(2x3)3(2x1);⑥y=7(3x),其中,y的值随x的增大而增大的函数是
;
y的值随x的增大而减小的函数是
;图象经过原点的函数是
.
【考点】一次函数的性质.
【分析】根据k>0,y随x的增大而增大,找出满足此条件的函数填入第一空;根据k<0,y随x的增大而减小,找出满足此条件的函数填入第二空;当b=0,图象过坐标原点,找出满足此条件的函数填入第三空.
【解答】①,③,⑥三个函数的一次项系数都大于0,所以它们的y的值都随x的增大而增大;②,④,⑤三个函数的一次项系数都小于0,所以它们的y的值都随x的增大而减小;
③,⑤为正比例函数,它们的图象都过原点.
故答案为:①,③,⑥;②,④,⑤;③,⑤.
【点评】本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.一次函数的图象是一条直线,当k>0,
y随x的增大而增大;当k<0,图象经过第二,四象限,y随x的增大而减小;当b=0,图象过坐标原点.
【夯实基础】
1、一次函数y=mx+n的图象如图所示,下列结论正确的是
( )
A.m=3,n=2
B.m=3,n=2
C.m=2,n=3
D.m=3,n=2
2、已知一次函数y=ax+b的图象如图所示,化简的结果为(
)
A.2ab
B.2a+b
C.b
D.b
3、一次函数y=(2m6)x7n+14的图象不经过第一象限,则m、n的取值范围是(
)
A.m<3,n>2
B.m<3,n>2
C.m<3,n>2
D.m<3,n>2
4、在同一坐标系中,作出两个一次函数y1=kx+b,y2=bx+k(b≠k)的图象正确的是( )
5、已知点A(x1,y1),B(x2,y2)是一次函数y=+17图象上的点,当x1>x2时,
则y1
y2(填“>”、“=”、“<”).
6、已知一次函数y=kx+k2+0.2,则该函数的图象一定经过第
象限.
7、若2y+3与3x7成正比例,则y是x的
函数.
8、已知一次函数y=(123m)x(186n),根据下列条件确定m、n的值.
(1)y随x
的增大而增大;
(2)图象不经过第三象限;
(3)图象经过原点;
(4)图象平行于直线y=3x+5;
(5)图象与y轴的交点在x轴的上方.
9、已知一次函数y=3x+6.
(1)在如图所示的平面直角坐标系中,画出该函数的图象;
(2)求图象分别与x轴,y轴的交点A,B的坐标;
(3)在(2)的条件下,点P是直线AB上的一个动点,
求OP的最小值;
(4)利用图象直接写出,当y<0时,x的取值范围.
【提优特训】
10、一条直线y=kx+b,其中2k+b=5和3k+b=6,则此函数经过的两点是
(
)
A.(2,5)和(3,6)
B.(2,5)和(3,6)
C.(2,5)和(3,6)
D.(2,5)和(3,6)
11、已知a、b、c均为实数,且a+b+c=0,a
有意义,则正比例函数y=(k2)x与一次函数y=(2k)x+k2的图象可能是( )
13、一次函数y=mx的图象经过点A(0,6
),这个函数的图象一定经过的象限为(
)
A.一、二
B.二、四
C.一、三
D.三、四
14、(1)一次函数y=(5m11)x+3m6的图象与y轴的交点在x轴的上方且y随x的增大而减小,则m
的取值范围是???
.
(2)已知直线y1=(3a2)x5a+7和直线y2=(5a7)x+2a+21的图象相交于点在y轴上,则a=
.
15、下列直线中,能与直线y=5x7平行的是:①y=5x;②y=7x5;③y=5x+1;④y=5x7;
⑤y=35
x
(填序号).
16、定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成长方形的周长与面积在数量上相等,则这个点叫做和谐点.
(1)判断点M(3,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,6)在直线y=xb(b为常数)上,试求a,b的值.
???
?
?
17、已知,如图A点的坐标为(,0),B点坐标为(0,2).
(1)求直线AB的直线解析式;
(2)过B点作直线BP与x轴交于点P,
若S△ABP=2S△AOB,求点P的坐标.
18、已知直线y1=和y2=的图象交于点A(8,7),且分别与y轴相交于B、C两点.
(1)画出符合题意的图形;
(2)求这两条直线的解析式;
(3)求△ABC的周长和面积.
【中考链接】
19、(2019?毕节)已知一次函数y=kx+b(k、b为常数,k≠0)的图象经过一、三、四象限,则下列结论正确的是(
)
A.kb>0
B.kb<0
C.k+b>0
D.k+b<0
20、(2019?扬州)若点P在一次函数y=x+4的图像上,则点P一定不在第( )象限.
A.第一象限
B.第二象限
C.第三象限
D.第四象限
21、(2019?杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )
22、(2019?成都)已知一次函数y=(k3)x+1的图象经过第一、二、四象限,则k的取值范围是
.
参考答案
1、D
2、D
3、A
4、B
5、<
6、一、二
7、一次
10、B
11、C
12、A
13、B
14、(1)
(2)
2
15、①③⑤
19、A
20、C
21、A
22、k<3
8、已知一次函数y=(123m)x(186n),根据下列条件确定m、n的值.
(1)y随x
的增大而增大;
(2)图象不经过第三象限;
(3)图象经过原点;
(4)图象平行于直线y=3x+5;
(5)图象与y轴的交点在x轴的上方.
解:(1)y随x的增大而增大,
则(123m)>0,b为任意实数;
∴m<4,b为任意实数;
(2)图象不经过第三象限,
(123m)<0且6b18>0;
∴m>4,且b>3;
(3)图象经过原点,
(123m)≠0且6b18=0,
∴m≠4,b=3;
(4)图象平行于直线y=3x+5
,
(123m)=3且6b18≠5;
∴m=5,b≠;
(5)图象与y轴的交点在x轴的上方.
则有两种情况:
①(123m)>0,6b18>0;
∴m<4,b>3,
②(123m)<0,6b18>0.
∴m>4,b>3.
9、已知一次函数y=3x+6.
(1)在如图所示的平面直角坐标系中,画出该函数的图象;
(2)求图象分别与x轴,y轴的交点A,B的坐标;
(3)在(2)的条件下,点P是直线AB上的一个动点,
求OP的最小值;
(4)利用图象直接写出,当y<0时,x的取值范围.
解:(1)令x=0,y=6;x=2,y=0,
∴一次函数y=3x+6经过A(2,0),B(0,6)两个特殊点,
∴该函数的图象如图所示:
(2)由(1)得图象分别与x轴,y轴的
交点A,B的坐标为(2,0),(0,6);
(3)当OP⊥AB时,OP的值最小,
在Rt△AOB中,OB=6,OA=2,
∴AB=,
∵S△AOB=,
∴
即2×6=×OP
OP=;
(4)由图象可得,当y<0时,x的取值范围是x>2.
16、定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成长方形的周长与面积在数量上相等,则这个点叫做和谐点.
(1)判断点M(3,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,6)在直线y=xb(b为常数)上,试求a,b的值.
解:(1)∵长方形的周长=2×(3+2)=10,
长方形的面积=3×2=6?,
长方形的周长≠长方形的面积,
???????
∴点M不是和谐点;
????????
∵长方形的周长=2×(4+4)=16,
长方形的面积=4×4=16?,
长方形的周长=长方形的面积,
???????
∴点N是和谐点.
(2)由题意:
???
?
?
2(+6)=6
???
??
解得:a=±3?,
????????
a=3时,将P
(3,6)代入得b=3
???????
?a=3时,将P
(3,6)代入得b=9.
17、已知,如图A点的坐标为(,0),B点坐标为(0,2).
(1)求直线AB的直线解析式;
(2)过B点作直线BP与x轴交于点P,
若S△ABP=2S△AOB,求点P的坐标.
解:设经过A,B两点的直线解析式
为y=kx+b(a、b为常数,a≠0),
根据题意,得0=k+b,2=b,
解得,k=,b=2,
∴过A,B两点的直线解析式为y=x2;
(2)设P点坐标为(x,0),
∵S△ABP=2S△AOB,依据图形得×2×()=2××2×,
解得,x=±2.5,
∴P点坐标分别为P1(2.5,0),P2(5,0).
18、已知直线y1=和y2=的图象交于点A(8,7),且分别与y轴相交于B、C两点.
(1)画出符合题意的图形;
(2)求这两条直线的解析式;
(3)求△ABC的周长和面积.
解:(1)将点A(8,7)代入y1=和
y2=中,得
7=,7=
解得m=22,n=1,
∴这两条直线的解析式为:y1=和y2=;
(2)过点A作AD垂直x轴于点D,作AE垂直y轴于点E,
∵A点的坐标为(8,7),
∴AD=OE=7,AE=OD=8,
令x=0,则y1=22,y2=1,
∴OB=22,OC=1∴CE=OEOC=71=6,∴BC=OBOC=221=21,
∴EB=OBOE=227=15.
在Rt△AEC中,AC=,
在Rt△AEB中,AB=,
∴△ABC的周长为AB+BC+CA=17+21+10=48;
△ABC的面积为
第9题图
第2题图
A
B
C
D
A
B
C
D
第17题图
A
B
C
D
第18题图
第17题图
第9题图
A
B
C
D
第9题图
第1题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
