3.3.5 相遇、追及问题
文档属性
| 名称 | 3.3.5 相遇、追及问题 |

|
|
| 格式 | rar | ||
| 文件大小 | 347.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-14 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
义务教育课程标准实验教科书
七年级上册
人民教育出版社出版 王斌制作
运用方程解决实际问题的一般过程是什么?
1、审题:分析题意,找出题中的数量及其关系;
2、设元:选择一个适当的未知数用字母表示(例如x);
3、列方程:根据相等关系列出方程;
4、解方程:求出未知数的值;
5、检验:检查求得的值是否正确和符合实际情形,并写出答案。
审
设
列
解
验
6、答:把所求的答案答出来。
答
行程问题中的基本关系量有哪些?它们有什么关系?
=
路程
时间
速度
×
路程
时间
速度
=
÷
速度
路程
时间
=
÷
探究:行程问题
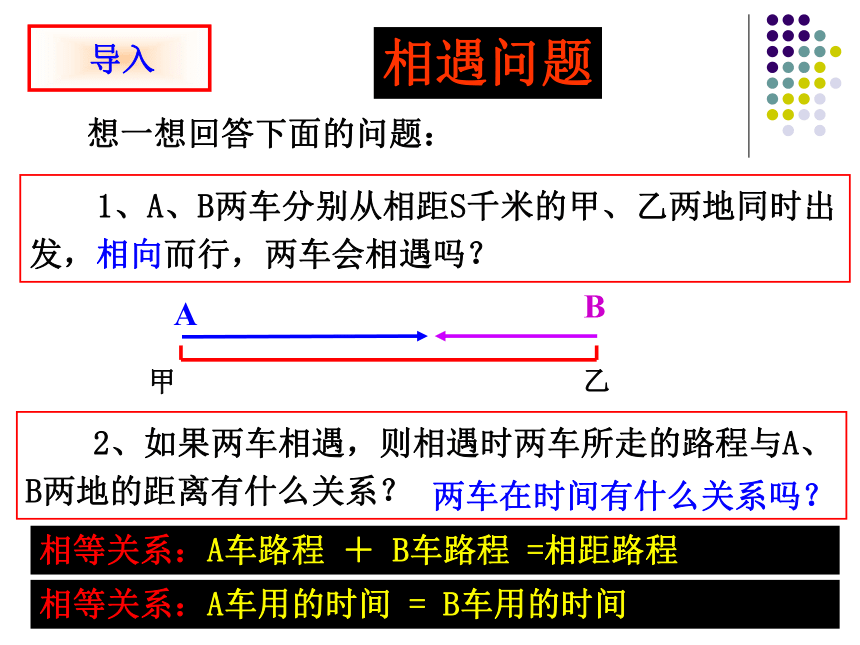
相等关系:A车路程 + B车路程 =相距路程
想一想回答下面的问题:
1、A、B两车分别从相距S千米的甲、乙两地同时出发,相向而行,两车会相遇吗?
导入
甲
乙
A
B
2、如果两车相遇,则相遇时两车所走的路程与A、B两地的距离有什么关系?
相遇问题
两车在时间有什么关系吗?
相等关系:A车用的时间 = B车用的时间
分 析
精讲 例题
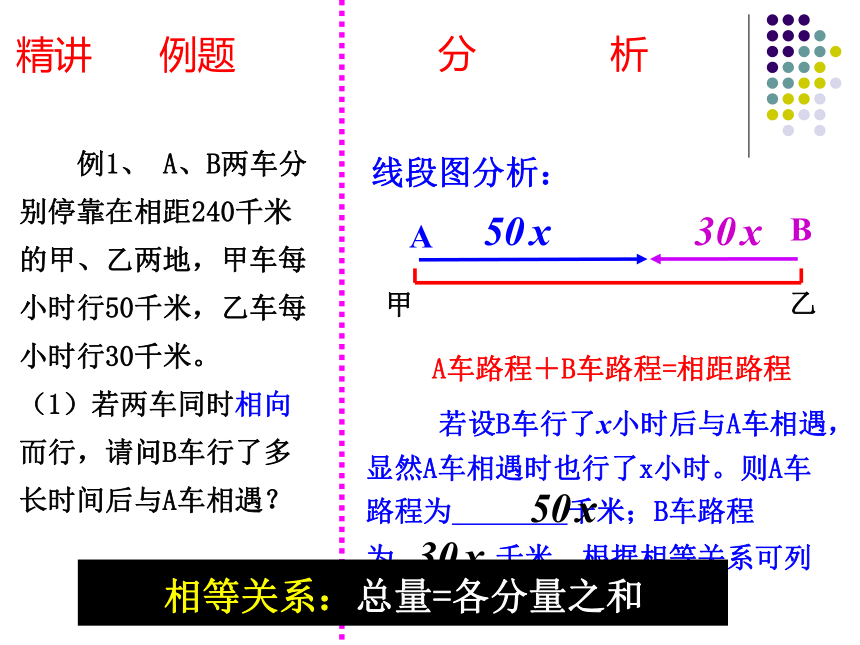
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
A车路程+B车路程=相距路程
线段图分析:
若设B车行了x小时后与A车相遇,显然A车相遇时也行了x小时。则A车路程为 千米;B车路程
为 千米。根据相等关系可列出方程。
相等关系:总量=各分量之和
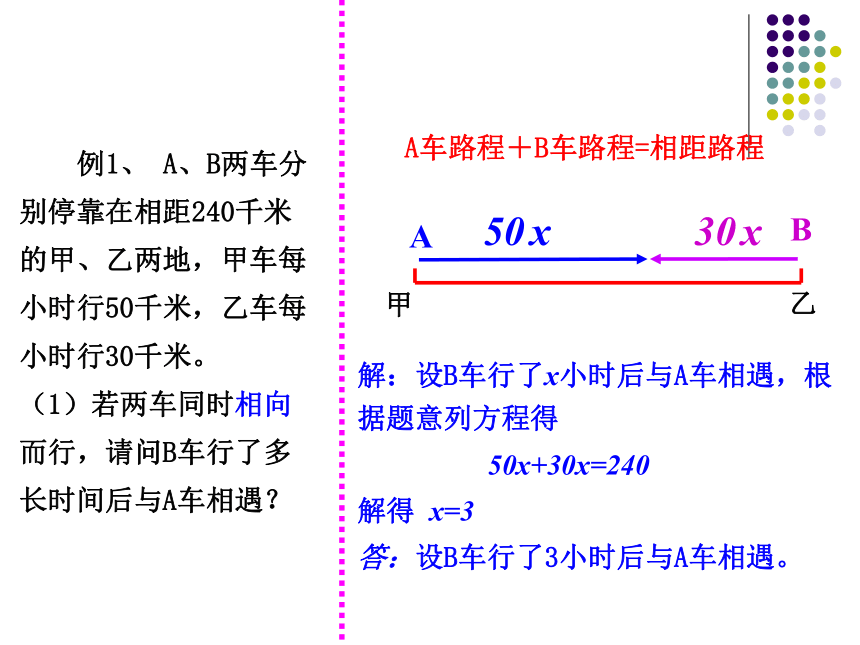
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
A车路程+B车路程=相距路程
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x=240
解得 x=3
答:设B车行了3小时后与A车相遇。
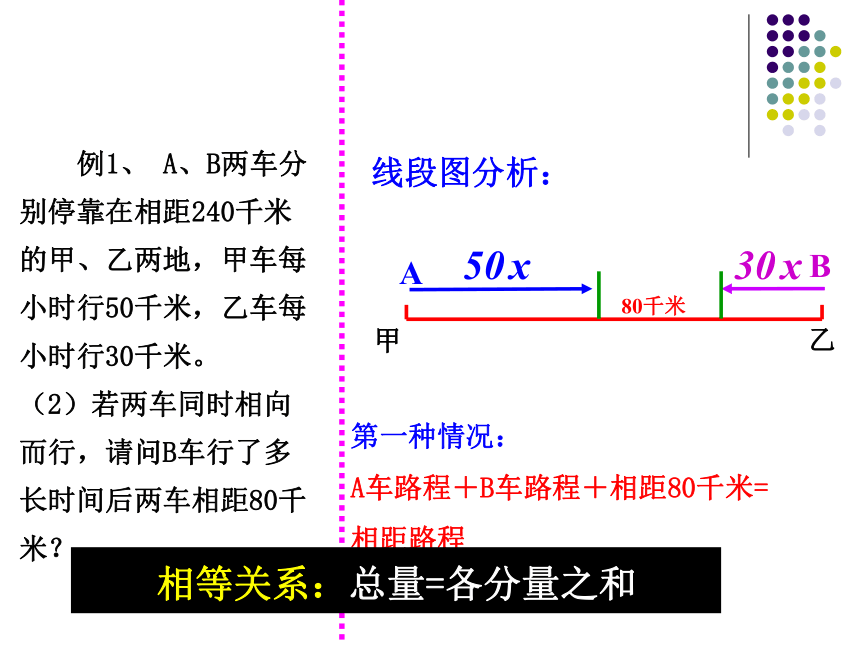
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
甲
乙
A
B
80千米
第一种情况:
A车路程+B车路程+相距80千米=
相距路程
相等关系:总量=各分量之和
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
甲
乙
A
B
80千米
第二种情况:
A车路程+B车路程-相距80千米=
相距路程
1、 A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(1)若两车相向而行,请问B车行了多长时间后与A车相遇?
相等关系:A车路程+A车同走的路程+ B车同走的路程=相距路程
线段图分析:
甲
乙
A
B
只设未知数,列方程,不解方程
甲、乙骑自行车同时从相距 65千米的两地相向而行,2小时相遇。甲比乙每小时多骑2.5千米,求乙的时速。
练习1
想一想回答下面的问题:
3、如果两车同向而行,B车先出发a小时,在什么情况下两车能相遇?为什么?
A车速度〉乙车速度
4、如果A车能追上B车,你能画出线段图吗?
甲
乙
A(B)
相等关系:
B车先行路程 + B车后行路程 =A车路程
家
学 校
追 及 地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
相等关系:
小明先行路程 + 小明后行路程 =爸爸的路程
家
学 校
追 及 地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
(1)解:设爸爸要 x分钟才追上小明,依题意得:
180x = 80x + 5×80
解得 x=4
答:爸爸追上小明用了4分钟。
2、 A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
若两车同向而行(B车在A车前面),请问B车行了多长时间后被A车追上?
线段图分析:
甲
A
B
50×1.5
50x
30x
乙
115
相等关系:
A车先行路程 + A车后行路程 - B车路程 = 115
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(1)反向
相等关系:
小王路程 + 叔叔路程 = 400
叔叔
小王
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑4米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(2)同向
相等关系:
小王路程 + 400 = 叔叔路程
叔叔
小王
归纳:
在列一元一次方程解行程问题时,我们常画出线段图来分析数量关系。用线段图来分析数量关系能够帮助我们更好的理解题意,找到适合题意的等量关系式,设出适合的未知数,列出方程。正确地作出线段图分析数量关系,能使我们分析问题和解问题的能力得到提高。
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
小结:这节课我们复习了行程问题中的相遇和追及问题,归纳如下:
相遇
A车路程
B车路程
相等关系:A车路程+B车路程=相距路程
A车后行路程
B车追击路程
A车先行路程
追击
相等关系:
B车路程=A车先路程+A车后行路程
或B车路程=A车路程+相距路程
义务教育课程标准实验教科书
七年级上册
人民教育出版社出版 王斌制作
运用方程解决实际问题的一般过程是什么?
1、审题:分析题意,找出题中的数量及其关系;
2、设元:选择一个适当的未知数用字母表示(例如x);
3、列方程:根据相等关系列出方程;
4、解方程:求出未知数的值;
5、检验:检查求得的值是否正确和符合实际情形,并写出答案。
审
设
列
解
验
6、答:把所求的答案答出来。
答
行程问题中的基本关系量有哪些?它们有什么关系?
=
路程
时间
速度
×
路程
时间
速度
=
÷
速度
路程
时间
=
÷
探究:行程问题
相等关系:A车路程 + B车路程 =相距路程
想一想回答下面的问题:
1、A、B两车分别从相距S千米的甲、乙两地同时出发,相向而行,两车会相遇吗?
导入
甲
乙
A
B
2、如果两车相遇,则相遇时两车所走的路程与A、B两地的距离有什么关系?
相遇问题
两车在时间有什么关系吗?
相等关系:A车用的时间 = B车用的时间
分 析
精讲 例题
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
A车路程+B车路程=相距路程
线段图分析:
若设B车行了x小时后与A车相遇,显然A车相遇时也行了x小时。则A车路程为 千米;B车路程
为 千米。根据相等关系可列出方程。
相等关系:总量=各分量之和
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
A车路程+B车路程=相距路程
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x=240
解得 x=3
答:设B车行了3小时后与A车相遇。
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
甲
乙
A
B
80千米
第一种情况:
A车路程+B车路程+相距80千米=
相距路程
相等关系:总量=各分量之和
例1、 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
线段图分析:
甲
乙
A
B
80千米
第二种情况:
A车路程+B车路程-相距80千米=
相距路程
1、 A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(1)若两车相向而行,请问B车行了多长时间后与A车相遇?
相等关系:A车路程+A车同走的路程+ B车同走的路程=相距路程
线段图分析:
甲
乙
A
B
只设未知数,列方程,不解方程
甲、乙骑自行车同时从相距 65千米的两地相向而行,2小时相遇。甲比乙每小时多骑2.5千米,求乙的时速。
练习1
想一想回答下面的问题:
3、如果两车同向而行,B车先出发a小时,在什么情况下两车能相遇?为什么?
A车速度〉乙车速度
4、如果A车能追上B车,你能画出线段图吗?
甲
乙
A(B)
相等关系:
B车先行路程 + B车后行路程 =A车路程
家
学 校
追 及 地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
相等关系:
小明先行路程 + 小明后行路程 =爸爸的路程
家
学 校
追 及 地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
(1)解:设爸爸要 x分钟才追上小明,依题意得:
180x = 80x + 5×80
解得 x=4
答:爸爸追上小明用了4分钟。
2、 A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
若两车同向而行(B车在A车前面),请问B车行了多长时间后被A车追上?
线段图分析:
甲
A
B
50×1.5
50x
30x
乙
115
相等关系:
A车先行路程 + A车后行路程 - B车路程 = 115
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(1)反向
相等关系:
小王路程 + 叔叔路程 = 400
叔叔
小王
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑4米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
(2)同向
相等关系:
小王路程 + 400 = 叔叔路程
叔叔
小王
归纳:
在列一元一次方程解行程问题时,我们常画出线段图来分析数量关系。用线段图来分析数量关系能够帮助我们更好的理解题意,找到适合题意的等量关系式,设出适合的未知数,列出方程。正确地作出线段图分析数量关系,能使我们分析问题和解问题的能力得到提高。
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
小结:这节课我们复习了行程问题中的相遇和追及问题,归纳如下:
相遇
A车路程
B车路程
相等关系:A车路程+B车路程=相距路程
A车后行路程
B车追击路程
A车先行路程
追击
相等关系:
B车路程=A车先路程+A车后行路程
或B车路程=A车路程+相距路程
