人教高中数学必修五2.5-等比数列的前n项和 课件(共15张PPT)
文档属性
| 名称 | 人教高中数学必修五2.5-等比数列的前n项和 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 683.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 21:29:33 | ||
图片预览






文档简介
(共15张PPT)
2.5
等比数列的前n项和
复习:等比数列
{an}
(1)
等比数列:
(2)
通项公式:
(4)
重要性质:
n-m
an=
am?
q
m+n=p+q
an
?aq
?am
=
ap
注:以上
m,
n,
p,
q
均为自然数
成等比数列
(3)
an+1
an
=q
(定值)
an=a1?
q
n-1
(4)
数列通项与前n项和的关系:
an=
S1
Sn-Sn-1
(
n=1)
(
n≥2)
已知an求Sn
探求等比数列求和的方法
问题:已知等比数列
,
公比为q,
求:
思考:
⑴×q,
得
⑵
⑴-⑵,得
由此得q≠1时,
等比数列的前n项和
设等比数列
它的前n项和是
⑴
即
说明:这种求和方法称为错位相减法
当q≠1时,
∵
∴
显然,当q=1时,
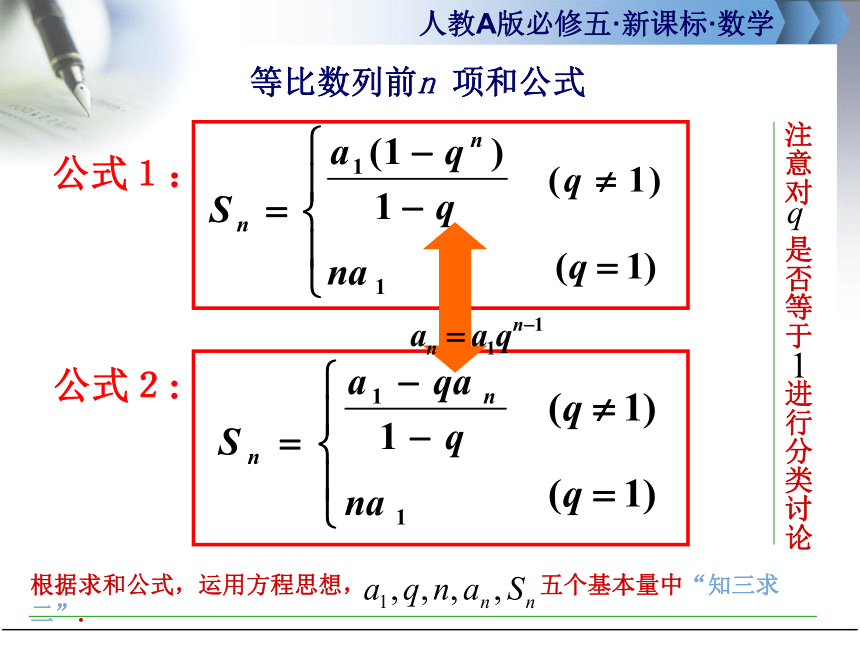
等比数列前n
项和公式
公式2:
公式1:
根据求和公式,运用方程思想,
五个基本量中“知三求二”.
注意对
是否等于
进行分类讨论
练习1.
根据下列条件,求相应的等比数列
的
例1、求下列等比数列前8项的和
例3.?某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第1年起,约几年内可使总销售量达到30000台(保留到个位)?
解:根据题意,每年销售量比上一年增加的百分率相同,
所以从第1年起,每年的销售量组成一个等比数列
{
}
其中
可得:
可得:
两边取对数,得:
利用计算器得:
(年)
答:约5年内可以使总销售量达到30000台。
练习2.
求等比数列
1,2,4,…从第5项到第10项的和.
从第5项到第10项的和:
求等比数列
从第3项到第7项的和.
从第3项到第7项的和:
练习3.
①
②
1、求和公式
当q≠1时,
当q=1时,
①注意分类讨论的思想!
等比数列求和时必须弄清q=1还是q≠1.
②运用方程的思想,五个量“知三求二”.
2、公式的推导方法
强调:
(重在过程)
③注意运用整体运算的思想.
小结
2.5
等比数列的前n项和
复习:等比数列
{an}
(1)
等比数列:
(2)
通项公式:
(4)
重要性质:
n-m
an=
am?
q
m+n=p+q
an
?aq
?am
=
ap
注:以上
m,
n,
p,
q
均为自然数
成等比数列
(3)
an+1
an
=q
(定值)
an=a1?
q
n-1
(4)
数列通项与前n项和的关系:
an=
S1
Sn-Sn-1
(
n=1)
(
n≥2)
已知an求Sn
探求等比数列求和的方法
问题:已知等比数列
,
公比为q,
求:
思考:
⑴×q,
得
⑵
⑴-⑵,得
由此得q≠1时,
等比数列的前n项和
设等比数列
它的前n项和是
⑴
即
说明:这种求和方法称为错位相减法
当q≠1时,
∵
∴
显然,当q=1时,
等比数列前n
项和公式
公式2:
公式1:
根据求和公式,运用方程思想,
五个基本量中“知三求二”.
注意对
是否等于
进行分类讨论
练习1.
根据下列条件,求相应的等比数列
的
例1、求下列等比数列前8项的和
例3.?某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第1年起,约几年内可使总销售量达到30000台(保留到个位)?
解:根据题意,每年销售量比上一年增加的百分率相同,
所以从第1年起,每年的销售量组成一个等比数列
{
}
其中
可得:
可得:
两边取对数,得:
利用计算器得:
(年)
答:约5年内可以使总销售量达到30000台。
练习2.
求等比数列
1,2,4,…从第5项到第10项的和.
从第5项到第10项的和:
求等比数列
从第3项到第7项的和.
从第3项到第7项的和:
练习3.
①
②
1、求和公式
当q≠1时,
当q=1时,
①注意分类讨论的思想!
等比数列求和时必须弄清q=1还是q≠1.
②运用方程的思想,五个量“知三求二”.
2、公式的推导方法
强调:
(重在过程)
③注意运用整体运算的思想.
小结
