北师大版数学七年级上册2.4 有理数的加法课件(第2课时 25张)
文档属性
| 名称 | 北师大版数学七年级上册2.4 有理数的加法课件(第2课时 25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 906.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 23:14:37 | ||
图片预览







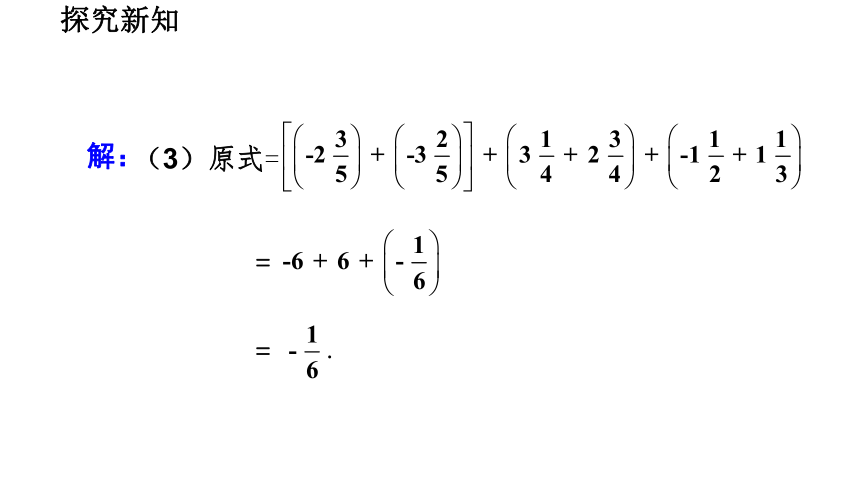

文档简介
2.4 有理数的加法
(第2课时)
导入新知
在小学中我们学过哪些加法的运算律?
加法交换律:两个数相加,交换加数的位置和不变.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
想一想 加法的运算律是不是也可以扩充到有理数范围?
素养目标
1.掌握有理数加法的运算律,能正确运用加法运算律简化运算 .
2.能运用有理数加法及其运算律解决生活中的实际问题.
3.培养观察、比较、归纳及运算能力,进一步培养协作学习的能力.
探究新知
知识点
有理数加法的运算律
计算并比较每组的两个算式的结果:
(1)(-8)+(-9)= (-9)+(-8)=
(2) 4 +(-7)= (-7) + 4 =
你发现了什么?
(3) [2+(-3)]+(-8)= 2+[(-3)+(-8)]=
(4) [10+(-10)]+(-5)= 10+[(-10)+(-5)]=
-17
-17
-3
-3
-9
-9
-5
-5
探究新知
加法的交换律:
a+b=b+a.
加法的结合律:
(a+b)+c=a+(b+c).
有理数加法的运算律
例1 计算:
探究新知
素养考点 1
运用加法运算律计算
(1)31+(-28)+28+69;
(2)(-64)+17+(-23)+68.
思考:有没有简便的方法?
(3) .
探究新知
(1)解:原式 =(31+69)+[(-28)+28]
(2) 解:原式=[(-64)+(-23)]?+(17+68)
(加法交换律和结合律)
=100+0
=100;
(加法的交换律和结合律)
=(-87)?+85
(一个数同0相加,仍得这个数)
=-2.
(异号相加法则)
探究新知
解:
(3)原式=
=
=
方法点拨
探究新知
使用运算律通常有下列情形:
(1)互为相反数的加数放在一起相加(相反数结合法);(2)能凑整的加数放在一起相加(凑整法);
(3)同号的加数放在一起相加(同号结合法) ;
(4)同分母或易于通分的分数放在一起相加(同分母结合法).
巩固练习
变式训练
计算(-12)+(+11)+(-8)+(-7)+(+39)+7.
解:原式=(+11)+ (+39)+ [ (-12)+(-8) ] +[ (-7)+7 ]
=50-20+0
=30.
探究新知
有一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,结果如下表:
听号
1
2
3
4
5
质量/g
444
459
454
459
454
听号
6
7
8
9
10
质量/g
454
449
454
459
464
这10听罐头的总质量是多少?
素养考点 2
加法运算律的应用
例2
探究新知
解法一:这10听罐头的总质量为
444+459+454+459+454+454+449+454+459+464=4 550(g).
解法二:把超过标准质量的克数用正数表示,不足的用负数表示,列出10听罐头与标准质量的差值表:
听号
1
2
3
4
5
与标准质量的差/g
听号
6
7
8
9
10
与标准质量的差/g
-10
5
5
0
0
0
0
-5
5
10
探究新知
这10听罐头与标准质量差值的和为
(-10)+ 5 + 0 + 5 + 0 + 0 +(-5)+ 0 + 5 + 10
=[(-10)+10]+[(-5)+5]+5+5=10(g).
因此,这10听罐头的总质量为
454×10 + 10 = 4 540 + 10 = 4 550(g).
方法点拨:分析问题,列出正确算式,之后运用加法运算律进行简单计算.
巩固练习
变式训练
每袋小麦的标准重量为90千克,10袋小麦称重(单位:千克)记录如下:91, 91, 91.5, 89, 91.2, 91.3, 88.7, 88.8, 91.8, 91.1.这10袋小麦的总重量是多少千克?如果每袋小麦以90千克为标准,这10袋小麦总计超过多少千克或不足多少千克?
巩固练习
解:每袋小麦超过90千克的部分记为正数,不足的千克数记作负数.10袋小麦对应的数分别为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.列出10袋小麦与标准质量的差值如下表所示.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1
2
3
4
5
6
7
8
9
10
1
2
1.5
-1
1.2
1.3
-1.3
-1.2
1.8
1.1
巩固练习
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
90×10+5.4=905.4(千克).
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4(千克)
这10袋小麦与标准质量的差值的和为
因此,这10袋小麦的总质量为
连接中考
(2019·广西壮族自治区)计算:(+45)+(-92)+35+(-8).
(+45)+(-92)+35+(-8)
=45+35-92-8
=80-100
=-20
解:
课堂检测
基础巩固题
1.(2019·长沙市长郡梅溪湖中学初一月考)7+(–3)+(–4)+18+(–11)=(7+18)+[(–3)+(–4)+(–11)]是应用了( )
A.加法交换律 B.加法结合律
C.分配律 D.加法交换律与结合律
D
课堂检测
基础巩固题
D
2.计算????????????+(+4.71)+????????????+(–6.71)的结果为( )
A.–2 B.3 C.–3 D.–1
?
课堂检测
基础巩固题
-50米
3.一潜艇所在高度为-80米,一条鲨鱼在潜艇上方30米处,则鲨鱼所在高度为________.
4.某种零件的直径规格是20±0.2mm,经检查,一个零件的直径18mm,该零件____________(填“合格”或“不合格”);
不合格
课堂检测
基础巩固题
5.小虫从某点O出发在一条直线上来回爬行,假定向右为正方向,爬行的记录如下(单位:厘米):+5、-3、+10、-8、-6、+12、-7.则小虫最终在起点O的 侧,距离点O 厘米处.
右
3
能力提升题
课堂检测
在2019个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是1,那么前6个数的和是 ,这2019个数的和是 .
0
2
拓广探索题
课堂检测
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推
(1)阴影部分的面积是多少?
(2)受此启发,你能求出 的值吗?
n
课堂检测
解:(1)部分①的面积为: ,
部分②的面积为:????????????=????????,
…
?
以此类推,部分 的面积????????????,
?
所以阴影部分面积为????????????或????????????;
?
(2)由图可得,原式=1+1?????????????=2?????????????=????????????????????.
?
○
有理数的加法运算律
3.同分母的分数相加
课堂小结
1.互为相反数的两个数先相加
5.易于通分的数可先相加
4.符号相同的正数或负数相加
2.相加能得整数的数可先相加
使用运算律的情形
运算律
1.加法交换律: a+b=b+a
2.加法结合律:(a+b)+c=a+(b+c)
(第2课时)
导入新知
在小学中我们学过哪些加法的运算律?
加法交换律:两个数相加,交换加数的位置和不变.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
想一想 加法的运算律是不是也可以扩充到有理数范围?
素养目标
1.掌握有理数加法的运算律,能正确运用加法运算律简化运算 .
2.能运用有理数加法及其运算律解决生活中的实际问题.
3.培养观察、比较、归纳及运算能力,进一步培养协作学习的能力.
探究新知
知识点
有理数加法的运算律
计算并比较每组的两个算式的结果:
(1)(-8)+(-9)= (-9)+(-8)=
(2) 4 +(-7)= (-7) + 4 =
你发现了什么?
(3) [2+(-3)]+(-8)= 2+[(-3)+(-8)]=
(4) [10+(-10)]+(-5)= 10+[(-10)+(-5)]=
-17
-17
-3
-3
-9
-9
-5
-5
探究新知
加法的交换律:
a+b=b+a.
加法的结合律:
(a+b)+c=a+(b+c).
有理数加法的运算律
例1 计算:
探究新知
素养考点 1
运用加法运算律计算
(1)31+(-28)+28+69;
(2)(-64)+17+(-23)+68.
思考:有没有简便的方法?
(3) .
探究新知
(1)解:原式 =(31+69)+[(-28)+28]
(2) 解:原式=[(-64)+(-23)]?+(17+68)
(加法交换律和结合律)
=100+0
=100;
(加法的交换律和结合律)
=(-87)?+85
(一个数同0相加,仍得这个数)
=-2.
(异号相加法则)
探究新知
解:
(3)原式=
=
=
方法点拨
探究新知
使用运算律通常有下列情形:
(1)互为相反数的加数放在一起相加(相反数结合法);(2)能凑整的加数放在一起相加(凑整法);
(3)同号的加数放在一起相加(同号结合法) ;
(4)同分母或易于通分的分数放在一起相加(同分母结合法).
巩固练习
变式训练
计算(-12)+(+11)+(-8)+(-7)+(+39)+7.
解:原式=(+11)+ (+39)+ [ (-12)+(-8) ] +[ (-7)+7 ]
=50-20+0
=30.
探究新知
有一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,结果如下表:
听号
1
2
3
4
5
质量/g
444
459
454
459
454
听号
6
7
8
9
10
质量/g
454
449
454
459
464
这10听罐头的总质量是多少?
素养考点 2
加法运算律的应用
例2
探究新知
解法一:这10听罐头的总质量为
444+459+454+459+454+454+449+454+459+464=4 550(g).
解法二:把超过标准质量的克数用正数表示,不足的用负数表示,列出10听罐头与标准质量的差值表:
听号
1
2
3
4
5
与标准质量的差/g
听号
6
7
8
9
10
与标准质量的差/g
-10
5
5
0
0
0
0
-5
5
10
探究新知
这10听罐头与标准质量差值的和为
(-10)+ 5 + 0 + 5 + 0 + 0 +(-5)+ 0 + 5 + 10
=[(-10)+10]+[(-5)+5]+5+5=10(g).
因此,这10听罐头的总质量为
454×10 + 10 = 4 540 + 10 = 4 550(g).
方法点拨:分析问题,列出正确算式,之后运用加法运算律进行简单计算.
巩固练习
变式训练
每袋小麦的标准重量为90千克,10袋小麦称重(单位:千克)记录如下:91, 91, 91.5, 89, 91.2, 91.3, 88.7, 88.8, 91.8, 91.1.这10袋小麦的总重量是多少千克?如果每袋小麦以90千克为标准,这10袋小麦总计超过多少千克或不足多少千克?
巩固练习
解:每袋小麦超过90千克的部分记为正数,不足的千克数记作负数.10袋小麦对应的数分别为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.列出10袋小麦与标准质量的差值如下表所示.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1
2
3
4
5
6
7
8
9
10
1
2
1.5
-1
1.2
1.3
-1.3
-1.2
1.8
1.1
巩固练习
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
90×10+5.4=905.4(千克).
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4(千克)
这10袋小麦与标准质量的差值的和为
因此,这10袋小麦的总质量为
连接中考
(2019·广西壮族自治区)计算:(+45)+(-92)+35+(-8).
(+45)+(-92)+35+(-8)
=45+35-92-8
=80-100
=-20
解:
课堂检测
基础巩固题
1.(2019·长沙市长郡梅溪湖中学初一月考)7+(–3)+(–4)+18+(–11)=(7+18)+[(–3)+(–4)+(–11)]是应用了( )
A.加法交换律 B.加法结合律
C.分配律 D.加法交换律与结合律
D
课堂检测
基础巩固题
D
2.计算????????????+(+4.71)+????????????+(–6.71)的结果为( )
A.–2 B.3 C.–3 D.–1
?
课堂检测
基础巩固题
-50米
3.一潜艇所在高度为-80米,一条鲨鱼在潜艇上方30米处,则鲨鱼所在高度为________.
4.某种零件的直径规格是20±0.2mm,经检查,一个零件的直径18mm,该零件____________(填“合格”或“不合格”);
不合格
课堂检测
基础巩固题
5.小虫从某点O出发在一条直线上来回爬行,假定向右为正方向,爬行的记录如下(单位:厘米):+5、-3、+10、-8、-6、+12、-7.则小虫最终在起点O的 侧,距离点O 厘米处.
右
3
能力提升题
课堂检测
在2019个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是1,那么前6个数的和是 ,这2019个数的和是 .
0
2
拓广探索题
课堂检测
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推
(1)阴影部分的面积是多少?
(2)受此启发,你能求出 的值吗?
n
课堂检测
解:(1)部分①的面积为: ,
部分②的面积为:????????????=????????,
…
?
以此类推,部分 的面积????????????,
?
所以阴影部分面积为????????????或????????????;
?
(2)由图可得,原式=1+1?????????????=2?????????????=????????????????????.
?
○
有理数的加法运算律
3.同分母的分数相加
课堂小结
1.互为相反数的两个数先相加
5.易于通分的数可先相加
4.符号相同的正数或负数相加
2.相加能得整数的数可先相加
使用运算律的情形
运算律
1.加法交换律: a+b=b+a
2.加法结合律:(a+b)+c=a+(b+c)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
