北师大版数学七年级上册2.6 有理数的加减混合运算课件(第3课时27张)
文档属性
| 名称 | 北师大版数学七年级上册2.6 有理数的加减混合运算课件(第3课时27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1020.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 00:00:00 | ||
图片预览







文档简介
2.6 有理数的加减混合运算
(第3课时)
导入新知
某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减/辆
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总生产量是多少?比原计划增加了还是减少了?增减数为多少?
导入新知
解:(1)+7﹣(﹣10)=17(辆).
(2)100×7+(﹣1+3﹣2+4+7﹣5﹣10)=696(辆),
700 ﹣696=4 (辆).
答:生产量最多的一天比生产量最少的一天多生产17辆.
答:本周总生产量是696辆,比原计划减少了4辆.
素养目标
1.熟悉在水位变化过程中出现的量,进一步加深对有理数意义的理解,巩固用有理数表示实际生活中的量. .
2.能综合运用有理数及其加法减法的有关知识,解决简单的实际问题,从中体会数学与现实生活的联系.
3.能用折线统计图描述实例的变化过程.
探究新知
知识点
有理数加减混合运算的应用
解: 最高水位可以记作35.3-33.4=+1.9(m).
最低水位可以记作11.5-33.4=-21.9(m).
平均水位可以记作22.6-33.4=-10.8(m).
小明家住在流花河旁,他查阅了历年来的水文资料(单位:m),看到流花河的一些水位数据:
如图所示,如果取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?
探究新知
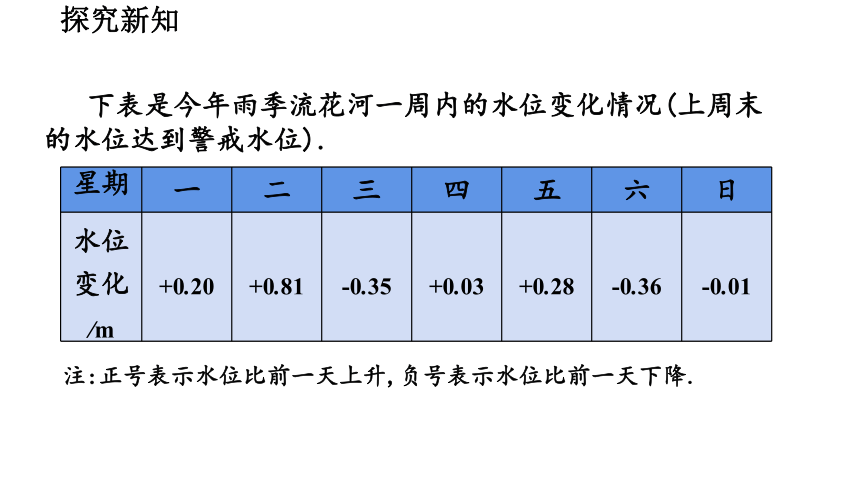
下表是今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位
变化
/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
探究新知
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
解: 本周每天的水位记录为
周一:33.4+0.20=33.60(m).
周二:33.4+0.20+0.81=34.41(m).
周五:33.4+0.20+0.81-0.35+0.03+0.28=34.37(m).
周三:33.4+0.20+0.81-0.35=34.06(m).
周四:33.4+0.20+0.81-0.35+0.03=34.09(m).
周日:33.4+0.20+0.81-0.35+0.03+0.28-0.36-0.01=34.00(m).
周六:33.4+0.20+0.81-0.35+0.03+0.28-0.36=34.01(m).
探究新知
所以周二的水位最高,周一的水位最低,它们都在警戒水位之上,其中最高水位与警戒水位的距离为34.41-33.4=1.01(m)或+0.2+0.81= 1.01(m);
最低水位与警戒水位的距离为33.6-33.4=0.2(m).
(2)与上周末相比,本周末河流水位是上升了还是下降了?
解:上周末的水位记录为33.40 m,
与上周末相比,本周末河流水位是上升了.
本周末的水位记录为34.00 m,
探究新知
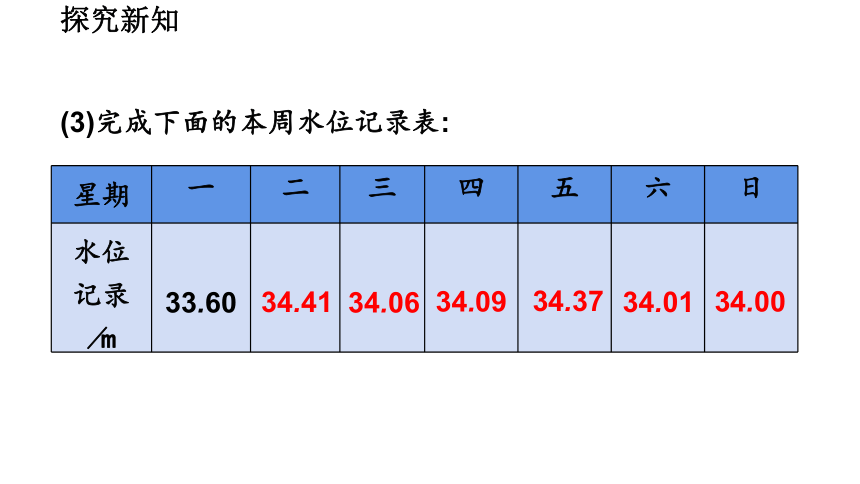
(3)完成下面的本周水位记录表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
星期
一
二
三
四
五
六
日
水位
记录
/m
33.60
?
?
?
?
?
?
34.41
34.06
34.09
34.37
34.01
34.00
探究新知
日
一
二
三
四
五
六
日
0.2
0.4
0.6
0.8
1.0
水位/m
星期
日
一
(4)以警戒水位为O点,用折线统计图表示本周的水位情况.
例 某商店一星期中每天的收支情况如下(收入为正,支出为负,单位:元):+17.85,-2.72,0,-41.28,-17.85,10.86,89.14.
则该商店这星期合计收入或支出多少元?
探究新知
素养考点
有理数加减混合运算的应用
解: +17.85+(-2.72)+0+(-41.28)+(-17.85)+10.86+89.14
=[+17.85+(-17.85)]+[(-2.72)+(-41.28)]+(10.86+89.14)
=0+(-44)+100
=+56(元).
答:该商店这星期合计收入56元.
方法点拨
探究新知
将有理数减法转化为加法时,要同时改变两个符号:一是运算符号减号变为加号,二是性质符号即减数变为它的相反数.有理数的加减混合运算应结合运算律和运算顺序进行运算.
巩固练习
变式训练
某一中学初一(2)班学生的平均身高是160厘米,
(1)下表给出了该班6名同学的身高情况(单位:厘米),试完成下表.
姓名
小明
小彬
小丽
小亮
小颖
小山
身高
159
154
165
身高与平均身高的差值
-1
+2
0
+3
(2)谁最高?谁最矮?
(3)最高与最矮的学生身高相差多少?
162
160
-6
+5
163
11厘米.
小山最高,小亮最矮.
连接中考
(2019·沈阳市第一三四中学初一月考)一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是 个单位.
50
课堂检测
基础巩固题
1.已知上周周五(周末不开盘)收盘时股市指数以2880点报收,本周内股市涨跌情况如下表所示,则本周四收盘时的股市指数为 ( )
A.2880 B.2877 C.2855 D.2887
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
星期
一
二
三
四
五
股指
变化
+50
-21
-100
+78
-78
D
课堂检测
基础巩固题
2.(2019·河南省初一期中)某运动员在东西走向的公路上练习跑步,跑步情况记录如下(向东为正,单位:米):1000,﹣1200,1100,﹣800,1400,该运动员跑的路程共为( )
A.1500米 B.5500米 C.4500米 D.3700米
B
课堂检测
基础巩固题
3.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测试的成绩是( )
A.90分 B.75分 C.91分 D.81分
C
-0.08
+0.09
+0.05
-0.05
+0.08
+0.06
课堂检测
基础巩固题
4.动物园在检验成年麦哲伦企鹅的身体状况时,最重要的一项工作就是称体重.已知某动物园对6只成年麦哲伦企鹅进行体重检测,以4kg为标准,超过或者不足的千克数分别用正数、负数表示,称重记录如下图所示,求这6只企鹅的总体重.
课堂检测
基础巩固题
4×6+0.15=24.15(kg).
-0.08
+0.09
+0.05
-0.05
+0.08
+0.06
解:(-0.08)+(+0.09)+(+0.05)+(-0.05)+(+0.08)+(+0.06)
=[(-0.08)+(+0.08)]+ [(-0.5)+0.5]+(0.09+0.06)
=0.15(kg).
答:这6只企鹅的总体重为24.15kg.
课堂检测
基础巩固题
5.南京出租车司机小李某一时段全是在中山东路上来回行驶,如果规定向东为正,向西为负,小李行车里程(单位:千米)为 15, -2, 5, -1, -10, -3, -2, 12, 4, -5.你能否知道在他将最后一位乘客送到目的地时,他距离出车的出发点有多远?
解:该出租车离出发点的距离为
15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4+( -5)=13(千米).
答:他距离出车的出发点13千米.
课堂检测
基础巩固题
6.某汽车制造厂计划前半年内每月生产汽车20辆,由于另有任务,每月上班人数有变化,1月至6月实际每月生产量和计划每月生产量相比,变化情况如下(增加为正,减少为负,单位:辆):+3,-2,-1,+4,+2,-5.
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
(2)前半年的实际总产量是多少?比计划的总产量多了还是少了?相差多少?
故生产量最多的一个月比生产量最少的一个月多生产了9辆;
解:(1)(+4)-(-5)=9(辆).
所以前半年实际总产量比原计划的总产量多了1辆.
(2)前半年实际总产量为
[(+3)+(-2)+(-1)+(+4)+(+2)+(-5)]
=1(辆).
能力提升题
课堂检测
小明的父亲上星期六买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
星期
一
二
三
四
五
六
每股变化
情况
+4
+4.5
-1
-2.5
-6
+2
(1)星期三收盘时,每股是多少元?
(2)本周内最高收盘价是每股多少元?最低收盘价是每股多少元?
(3)已知小明父亲买进股票时付了交易额1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果他在周六收盘时将全部股票卖出,他的收益情况如何?
能力提升题
课堂检测
解: 周一收盘每股价格为27+4=31(元),
周六收盘每股价格为26+2=28 (元).
周二收盘每股价格为31+4.5=35.5 (元),
周三收盘每股价格为35.5-1=34.5 (元),
周四收盘每股价格为34.5-2.5=32 (元),
周五收盘每股价格为32-6=26 (元),
能力提升题
课堂检测
则:(1)周三收盘时,每股是34.5元.
手续费和交易税共28000×(1.5‰+1‰)=70(元),
(2)本周收盘最高价是每股35.5元,最低收盘价是每股26元.
(3)买入时交易额为27×1000=27000(元),
手续费为27000×1.5‰=40.5(元),
卖出时交易额为28×1000=28000(元),
所以总收益为28000-27000-40.5-70=889.5(元).
拓广探索题
课堂检测
一家饭店,地面上18层,地下1层,地面上1楼为接待处,顶楼为公共设施处,其余16层为客房;地下1层为停车场.
(1)客房7楼与停车场相差几层楼?
解:记地上为正,地下1楼为0.
(1)7-0=7(层).
答:客房7楼与停车场相差7层楼.
拓广探索题
课堂检测
(2)某会议接待员把汽车停在停车场,进入该层电梯,往上14层,又下5层,再下3层,最后上6层,你知道他最后在哪里?
解:(2)0+14-5-3+6=12(层).
答:他最后在12层.
(3)某日,电梯检修,一服务生在停车场停好汽车后,只能走楼梯,他先去客房,依次到了8楼、接待处、4楼,又回接待处,最后回到停车场,他共走了几层楼梯?
解:(3)8+7+3+3+1=22(层).
答:他共走了22层楼梯.
有理数加减混合运算的应用
会用数学去解决生活中的变化现象,对于几次连续的变化情况可以用有理数的加减法去解决
借助表格折线统计图形象直观地反映事物的变化情况 .
课堂小结
很多实际问题可以转化为有理数的加减混合运算来解决,根据需要可以“人为”地规定零点.
(第3课时)
导入新知
某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减/辆
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总生产量是多少?比原计划增加了还是减少了?增减数为多少?
导入新知
解:(1)+7﹣(﹣10)=17(辆).
(2)100×7+(﹣1+3﹣2+4+7﹣5﹣10)=696(辆),
700 ﹣696=4 (辆).
答:生产量最多的一天比生产量最少的一天多生产17辆.
答:本周总生产量是696辆,比原计划减少了4辆.
素养目标
1.熟悉在水位变化过程中出现的量,进一步加深对有理数意义的理解,巩固用有理数表示实际生活中的量. .
2.能综合运用有理数及其加法减法的有关知识,解决简单的实际问题,从中体会数学与现实生活的联系.
3.能用折线统计图描述实例的变化过程.
探究新知
知识点
有理数加减混合运算的应用
解: 最高水位可以记作35.3-33.4=+1.9(m).
最低水位可以记作11.5-33.4=-21.9(m).
平均水位可以记作22.6-33.4=-10.8(m).
小明家住在流花河旁,他查阅了历年来的水文资料(单位:m),看到流花河的一些水位数据:
如图所示,如果取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?
探究新知
下表是今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位
变化
/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
探究新知
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
解: 本周每天的水位记录为
周一:33.4+0.20=33.60(m).
周二:33.4+0.20+0.81=34.41(m).
周五:33.4+0.20+0.81-0.35+0.03+0.28=34.37(m).
周三:33.4+0.20+0.81-0.35=34.06(m).
周四:33.4+0.20+0.81-0.35+0.03=34.09(m).
周日:33.4+0.20+0.81-0.35+0.03+0.28-0.36-0.01=34.00(m).
周六:33.4+0.20+0.81-0.35+0.03+0.28-0.36=34.01(m).
探究新知
所以周二的水位最高,周一的水位最低,它们都在警戒水位之上,其中最高水位与警戒水位的距离为34.41-33.4=1.01(m)或+0.2+0.81= 1.01(m);
最低水位与警戒水位的距离为33.6-33.4=0.2(m).
(2)与上周末相比,本周末河流水位是上升了还是下降了?
解:上周末的水位记录为33.40 m,
与上周末相比,本周末河流水位是上升了.
本周末的水位记录为34.00 m,
探究新知
(3)完成下面的本周水位记录表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
星期
一
二
三
四
五
六
日
水位
记录
/m
33.60
?
?
?
?
?
?
34.41
34.06
34.09
34.37
34.01
34.00
探究新知
日
一
二
三
四
五
六
日
0.2
0.4
0.6
0.8
1.0
水位/m
星期
日
一
(4)以警戒水位为O点,用折线统计图表示本周的水位情况.
例 某商店一星期中每天的收支情况如下(收入为正,支出为负,单位:元):+17.85,-2.72,0,-41.28,-17.85,10.86,89.14.
则该商店这星期合计收入或支出多少元?
探究新知
素养考点
有理数加减混合运算的应用
解: +17.85+(-2.72)+0+(-41.28)+(-17.85)+10.86+89.14
=[+17.85+(-17.85)]+[(-2.72)+(-41.28)]+(10.86+89.14)
=0+(-44)+100
=+56(元).
答:该商店这星期合计收入56元.
方法点拨
探究新知
将有理数减法转化为加法时,要同时改变两个符号:一是运算符号减号变为加号,二是性质符号即减数变为它的相反数.有理数的加减混合运算应结合运算律和运算顺序进行运算.
巩固练习
变式训练
某一中学初一(2)班学生的平均身高是160厘米,
(1)下表给出了该班6名同学的身高情况(单位:厘米),试完成下表.
姓名
小明
小彬
小丽
小亮
小颖
小山
身高
159
154
165
身高与平均身高的差值
-1
+2
0
+3
(2)谁最高?谁最矮?
(3)最高与最矮的学生身高相差多少?
162
160
-6
+5
163
11厘米.
小山最高,小亮最矮.
连接中考
(2019·沈阳市第一三四中学初一月考)一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是 个单位.
50
课堂检测
基础巩固题
1.已知上周周五(周末不开盘)收盘时股市指数以2880点报收,本周内股市涨跌情况如下表所示,则本周四收盘时的股市指数为 ( )
A.2880 B.2877 C.2855 D.2887
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
星期
一
二
三
四
五
股指
变化
+50
-21
-100
+78
-78
D
课堂检测
基础巩固题
2.(2019·河南省初一期中)某运动员在东西走向的公路上练习跑步,跑步情况记录如下(向东为正,单位:米):1000,﹣1200,1100,﹣800,1400,该运动员跑的路程共为( )
A.1500米 B.5500米 C.4500米 D.3700米
B
课堂检测
基础巩固题
3.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测试的成绩是( )
A.90分 B.75分 C.91分 D.81分
C
-0.08
+0.09
+0.05
-0.05
+0.08
+0.06
课堂检测
基础巩固题
4.动物园在检验成年麦哲伦企鹅的身体状况时,最重要的一项工作就是称体重.已知某动物园对6只成年麦哲伦企鹅进行体重检测,以4kg为标准,超过或者不足的千克数分别用正数、负数表示,称重记录如下图所示,求这6只企鹅的总体重.
课堂检测
基础巩固题
4×6+0.15=24.15(kg).
-0.08
+0.09
+0.05
-0.05
+0.08
+0.06
解:(-0.08)+(+0.09)+(+0.05)+(-0.05)+(+0.08)+(+0.06)
=[(-0.08)+(+0.08)]+ [(-0.5)+0.5]+(0.09+0.06)
=0.15(kg).
答:这6只企鹅的总体重为24.15kg.
课堂检测
基础巩固题
5.南京出租车司机小李某一时段全是在中山东路上来回行驶,如果规定向东为正,向西为负,小李行车里程(单位:千米)为 15, -2, 5, -1, -10, -3, -2, 12, 4, -5.你能否知道在他将最后一位乘客送到目的地时,他距离出车的出发点有多远?
解:该出租车离出发点的距离为
15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4+( -5)=13(千米).
答:他距离出车的出发点13千米.
课堂检测
基础巩固题
6.某汽车制造厂计划前半年内每月生产汽车20辆,由于另有任务,每月上班人数有变化,1月至6月实际每月生产量和计划每月生产量相比,变化情况如下(增加为正,减少为负,单位:辆):+3,-2,-1,+4,+2,-5.
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
(2)前半年的实际总产量是多少?比计划的总产量多了还是少了?相差多少?
故生产量最多的一个月比生产量最少的一个月多生产了9辆;
解:(1)(+4)-(-5)=9(辆).
所以前半年实际总产量比原计划的总产量多了1辆.
(2)前半年实际总产量为
[(+3)+(-2)+(-1)+(+4)+(+2)+(-5)]
=1(辆).
能力提升题
课堂检测
小明的父亲上星期六买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
星期
一
二
三
四
五
六
每股变化
情况
+4
+4.5
-1
-2.5
-6
+2
(1)星期三收盘时,每股是多少元?
(2)本周内最高收盘价是每股多少元?最低收盘价是每股多少元?
(3)已知小明父亲买进股票时付了交易额1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果他在周六收盘时将全部股票卖出,他的收益情况如何?
能力提升题
课堂检测
解: 周一收盘每股价格为27+4=31(元),
周六收盘每股价格为26+2=28 (元).
周二收盘每股价格为31+4.5=35.5 (元),
周三收盘每股价格为35.5-1=34.5 (元),
周四收盘每股价格为34.5-2.5=32 (元),
周五收盘每股价格为32-6=26 (元),
能力提升题
课堂检测
则:(1)周三收盘时,每股是34.5元.
手续费和交易税共28000×(1.5‰+1‰)=70(元),
(2)本周收盘最高价是每股35.5元,最低收盘价是每股26元.
(3)买入时交易额为27×1000=27000(元),
手续费为27000×1.5‰=40.5(元),
卖出时交易额为28×1000=28000(元),
所以总收益为28000-27000-40.5-70=889.5(元).
拓广探索题
课堂检测
一家饭店,地面上18层,地下1层,地面上1楼为接待处,顶楼为公共设施处,其余16层为客房;地下1层为停车场.
(1)客房7楼与停车场相差几层楼?
解:记地上为正,地下1楼为0.
(1)7-0=7(层).
答:客房7楼与停车场相差7层楼.
拓广探索题
课堂检测
(2)某会议接待员把汽车停在停车场,进入该层电梯,往上14层,又下5层,再下3层,最后上6层,你知道他最后在哪里?
解:(2)0+14-5-3+6=12(层).
答:他最后在12层.
(3)某日,电梯检修,一服务生在停车场停好汽车后,只能走楼梯,他先去客房,依次到了8楼、接待处、4楼,又回接待处,最后回到停车场,他共走了几层楼梯?
解:(3)8+7+3+3+1=22(层).
答:他共走了22层楼梯.
有理数加减混合运算的应用
会用数学去解决生活中的变化现象,对于几次连续的变化情况可以用有理数的加减法去解决
借助表格折线统计图形象直观地反映事物的变化情况 .
课堂小结
很多实际问题可以转化为有理数的加减混合运算来解决,根据需要可以“人为”地规定零点.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
