高一上学期物理(必修1)第4章综合检测B卷(含解析)
文档属性
| 名称 | 高一上学期物理(必修1)第4章综合检测B卷(含解析) |

|
|
| 格式 | DOC | ||
| 文件大小 | 507.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-02 15:49:54 | ||
图片预览




文档简介
第四章 牛顿运动定律综合检测(B卷)
(时间90分钟 满分100分)
一、选择题(本题共12小题,每小题4分,共48分。在每小题给出的四个选项中,第2、3、4、8、9、11小题,只有一个选项正确,第1、5、6、7、10、12小题,每题有多个选项正确,全部选对的得4分,选对而不全的得2分,错选或不选的得0分。)
1.[2014·山东莱芜一中高一期中]下列说法中正确的是( )
A.伽利略的理想实验说明物体的运动不需要力来维持
B. 牛顿第一定律说明力是改变物体运动状态的原因
C.同一汽车,速度越快,越难刹车,说明物体速度越大,惯性越大
D.已知月球上的重力加速度是地球上的,故一个物体从地球移到月球惯性减小为
解析:惯性是物体的一种属性,不随v变化,与质量有关,C、D错。
答案:AB
2. 下面是摘自上个世纪美国报纸上的一篇文章:阿波罗登月火箭在脱离地球飞向月球的过程中,宇航员通过无线电与在家中上小学的儿子汤姆通话。宇航员:“汤姆,我们现在已关闭了火箭上所有的发动机,正向月球飞去。”汤姆:“你们关闭了所有的发动机,那么靠什么力量推动火箭向前运动呢?”宇航员犹豫了半天,说:“我想大概是伽利略在推动火箭向前运动吧。”若不计天体对火箭的引力,由上述材料可知下列说法错误的是( )
A.汤姆问话所体现的物理思想是“力是维持物体运动的原因”
B. 宇航员答话所体现的物理思想是“力是维持物体运动的原因”
C.宇航员答话所体现的物理思想是“物体运动不需要力来维持”
D.宇航员答话的真实意思是火箭正在依靠惯性飞行
解析:汤姆问“靠什么力量推动火箭向前运动?”说明汤姆认为火箭向前运动必须有力的作用,即力是维持物体运动的原因,A正确。宇航员的回答提出伽利略,而伽利略的观点是力不是维持物体运动状态的原因,而是改变物体运动状态的原因,即运动不需要力来维持,物体具有保持原来运动状态的性质即惯性,答案C、D对。答案B错。
答案:B
3. 惯性制导系统已广泛应用于弹道式导弹工程中,这个系统的重要元件之一是加速度计。加速度计的构造原理的示意图如右图所示:沿导弹长度方向安装的固定光滑杆上套一质量为m的滑块,滑块两侧分别与劲度系数为k的弹簧相连;两弹簧的另一端与固定壁相连。滑块原来静止,弹簧处于自然长度。滑块上有指针,可通过标尺测出滑块的位移,然后通过控制系统进行制导。设某段时间内导弹沿水平方向运动,指针向左偏离O点的距离为x,则这段时间内导弹的加速度( )
A.方向向左,大小为kx/m B.方向向右,大小为kx/m
C.方向向左,大小为2kx/m D.方向向右,大小为2kx/m
解析:原来弹簧处于自然长度,后来指针向左偏离O点距离x,则左边弹簧压缩x,右边弹簧伸长x,滑块受的合力为2kx,方向向右。由牛顿第二定律:2kx=ma,加速度a=2kx/m,方向向右。
答案:D
4. [2014·杭州二中高一期中]“神舟九号”飞船与“天宫一号”空间站在太空中成功对接后稳定运行在预定的轨道上,其内部平台上的一台实验仪器处于失重状态,这时( )
A.如仪器是天平的话,就不能使用
B. 平台对仪器的弹力不为零
C.如仪器是弹簧秤的话,就不能使用
D.以上说法都不对
解析:处于完全失重状态,物体间接触但无力的作用,A对,B错。弹簧秤可测拉力,不能测物体的重力,C错。
答案:A
5. [2014·山西大学附中高一考试]气球吊着两个质量相同的重物A、B以10 m/s的速度匀速上升,两个重物之间用轻弹簧连接,重力加速度为g,若在距离地面上方10 m处绳子突然断裂,在断开瞬间有( )
A.vA=0 B.vB=10 m/s
C.aA=g D.aB=0
解析:设每个物体质量均为m,匀速上升时,绳上拉力FT=2mg,弹簧的弹力F=mg。绳子突然断裂的瞬间,两物体的速度没有改变,均为10 m/s,选项A错误、B正确;绳子的拉力消失,弹簧弹力没有变化,对A:F+mg=maA,得aA=2g,对B:因F=mg,故aB=0,选项C错误、D正确。
答案:BD
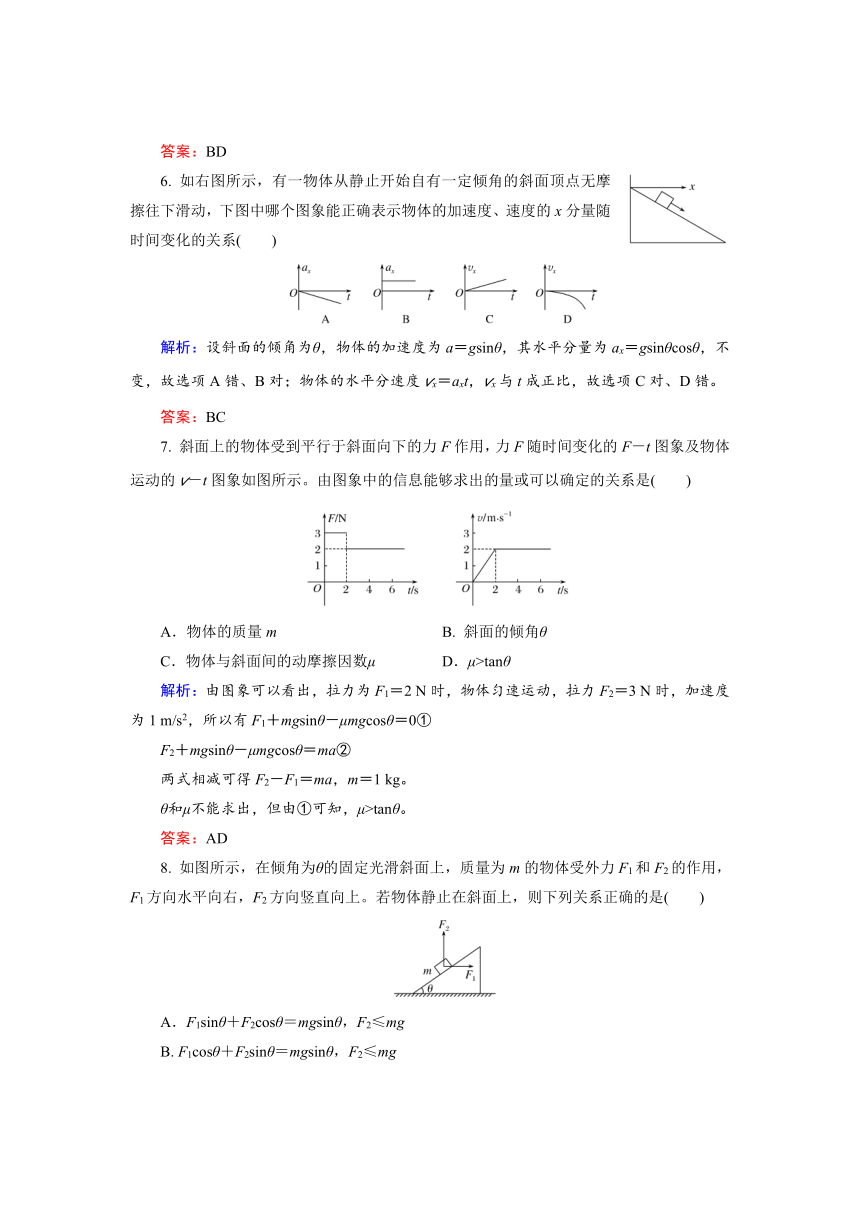
6. 如右图所示,有一物体从静止开始自有一定倾角的斜面顶点无摩擦往下滑动,下图中哪个图象能正确表示物体的加速度、速度的x分量随时间变化的关系( )
解析:设斜面的倾角为θ,物体的加速度为a=gsinθ,其水平分量为ax=gsinθcosθ,不变,故选项A错、B对;物体的水平分速度vx=axt,vx与t成正比,故选项C对、D错。
答案:BC
7. 斜面上的物体受到平行于斜面向下的力F作用,力F随时间变化的F-t图象及物体运动的v-t图象如图所示。由图象中的信息能够求出的量或可以确定的关系是( )
A.物体的质量m B. 斜面的倾角θ
C.物体与斜面间的动摩擦因数μ D.μ>tanθ
解析:由图象可以看出,拉力为F1=2 N时,物体匀速运动,拉力F2=3 N时,加速度为1 m/s2,所以有F1+mgsinθ-μmgcosθ=0①
F2+mgsinθ-μmgcosθ=ma②
两式相减可得F2-F1=ma,m=1 kg。
θ和μ不能求出,但由①可知,μ>tanθ。
答案:AD
8. 如图所示,在倾角为θ的固定光滑斜面上,质量为m的物体受外力F1和F2的作用,F1方向水平向右,F2方向竖直向上。若物体静止在斜面上,则下列关系正确的是( )
A.F1sinθ+F2cosθ=mgsinθ,F2≤mg
B. F1cosθ+F2sinθ=mgsinθ,F2≤mg
C.F1sinθ-F2cosθ=mgsinθ,F2≤mg
D.F1cosθ-F2sinθ=mgsinθ,F2≤mg
解析:对斜面上物体受力分析如图,建立以沿斜面方向为x轴,垂直斜面方向为y轴的坐标系,物体静止在斜面上,由平衡条件可得:沿x方向的合力为0:F1cosθ+F2sinθ=mgsinθ
如果考虑竖直方向合力为0:F2+Ncosθ=mg,F2≤mg可见,选择B。
答案:B
9. 某中学实验小组的同学在电梯的天花板上固定一根弹簧测力计,使其测量挂钩(跟弹簧相连的挂钩)向下,并在钩上悬挂一个重为10 N的钩码。弹簧测力计弹力随时间变化的规律如图所示,根据F-t图象,下列分析正确的是( )
A.从时刻t1到t2,钩码处于超重状态
B. 从时刻t3到t4,钩码处于失重状态
C.电梯可能开始停在15楼,先加速向下,接着匀速向下,再减速向下,最后停在1楼
D.电梯可能开始停在1楼,先加速向上,接着匀速向上,再减速向上,最后停在15楼
解析:0~t1阶段,物体处于平衡(静止或匀速)状态;t1~t2阶段,物体处于失重(加速下降或减速上升)状态;t2~t3阶段,物体处于平衡状态;t3~t4阶段,物体处于超重(加速上升或减速下降)状态,选项C正确。
答案:C
10. 一枚火箭由地面竖直向上发射,其速度和时间的关系图线如图所示,则( )
A.t3时刻火箭距地面最远
B.t2~t3的时间内,火箭在向下降落
C.t1~t2的时间内,火箭处于超重状态
D.0~t3的时间内,火箭始终处于失重状态
解析:本题考查对v-t图象的理解、超重、失重,分析时要由图象结合速度正负的意义、加速度正负的意义进行分析。速度始终为正值,说明火箭始终是向上运动的,故t3时刻火箭距地面最远,A选项正确,B选项错误;0~t2时间内,火箭加速上升,加速度向上,处于超重状态,t2~t3时间内火箭减速上升,加速度向下,处于失重状态,C选项正确,D选项错误。
答案:AC
11. 如右图所示,静止的倾斜传送带上有一木块正在匀速下滑,当传送带突然向上开动后,下列说法正确的是( )
A.木块所受摩擦力变大
B. 木块到底部所走位移变大
C.木块到底部所用时间变长
D.木块到底部所用的时间不变
解析:传送带静止和向上开动,两种情况下,物体受的滑动摩擦力的大小和方向都是相同的。所以物体的运动情况相同。到达底部所用的时间不变。
答案:D
12. 如图甲所示,某人正通过定滑轮将质量为m的货物提升到高处。滑轮的质量和摩擦均不计,货物获得的加速度a与绳子对货物竖直向上的拉力FT之间的函数关系如图乙所示。由图可以判断( )
A.图线与纵轴的交点M的值aM=-g
B. 图线与横轴的交点N的值FTN=mg
C.图线的斜率等于物体的质量m
D.图线的斜率等于物体质量的倒数
解析:由牛顿第二定律,有FT-mg=ma,故得a=-g,当FT=0时,a=-g,选项A正确;当a=0时,FT=mg,选项B正确;图线的斜率k=,选项D正确。
答案:ABD
二、填空题(本题共2小题,每小题5分,共10分。)
13. 依据“验证平行四边形定则”的实验,回答下列问题:
(1)在该实验中,合力与分力的概念是一种________的科学思想方法。
(2)某同学在做该实验时,弹簧测力计平行于木板如图放置,然后记录力的大小和方向,请你指出这样操作的问题:________________________________________。
解析:(1)等效替代
(2)弹簧测力计的轴线与细线套不在同一直线上,导致测量数据不准确。
答案:见解析
14. 在保持质量不变,探究加速度与物体受力间关系的实验中(使用教材提供的装置),小车质量M和砝码质量m分别选取下列四组值:
A.M=500 g,m分别为50 g、70 g、100 g、125 g
B.M=500 g,m分别为20 g、30 g、40 g、50 g
C.M=200 g,m分别为50 g、75 g、100 g、125 g
D.M=200 g,m分别为30 g、40 g、50 g、60 g
(1)如果其他操作都正确,那么在选用________组值测量时所画出的图线较准确。
(2)在选用此组值时,m取________时实验误差较大。
解析:在B组数据中,最容易满足小车质量M远大于砝码质量m的条件。
答案:(1)B (2)50 g
三、计算题(本题共4小题,共42分。要有必要的文字说明和演算步骤。有数值计算的题注明单位。)
15. (10分)[2014·南阳市五校联考高一期中]如图所示,一重为200 N的物体静止于水平地面上,若用一劲度系数为20 N/cm的轻质弹簧水平拉此物体,当弹簧的伸长量为4 cm时,物体恰在水平面上做匀速直线运动。求:
(1)弹簧弹力的大小;
(2)物体与水平面间的动摩擦因数。
解析:(1)由F=kx得
F=kx=20×102×4×10-2 N=80 N。
(2)由题意可知,物体匀速运动,弹簧的拉力与摩擦力相等,所以F=f
又∵f=μFN=μG
∴μ=0.4。
答案:(1)80 N (2)0.4
16. (10分)科研人员乘气球进行科学考察,气球、座舱、压舱物和科研人员的总质量为990 kg。气球在空中停留一段时间后,发现气球漏气而下降,及时堵住。堵住时气球下降速度为1 m/s,且做匀加速运动,4 s内下降了12 m。为使气球安全着陆,向舱外缓慢抛出一定的压舱物。此后发现气球做匀减速运动,下降速度在5分钟内减少了3 m/s。若空气阻力和泄漏气体的质量均可忽略,重力加速度g取9.89 m/s2,求抛掉的压舱物的质量。
解析:设堵住漏洞后,气球的初速度为v0,所受的空气浮力为f,气球、座舱、压舱物和科研人员的总质量为m,由牛顿第二定律得mg-f=ma ①
式中a是气球下降的加速度,以此加速度在时间t内下降了h,则
h=v0t+at2 ②
当向舱外抛掉质量为m′的压舱物后,有
f-(m-m′)g=(m-m′)a′ ③
式中a′是抛掉压舱物后气球的加速度,由题意,此时a′方向向上
Δv=a′Δt ④
式中Δv是抛掉压舱物后在Δt时间内下降速度的减少量。由①③得
m′=m ⑤
将题设数据
m=990 kg,v0=1 m/s,t=4 s,h=12 m,Δt=300 s,
Δv=3 m/s,g=9.89 m/s2
代入②④⑤式得m′=101 kg。 ⑥
答案:101 kg
17. (10分)如图所示,一个滑雪运动员,滑板和人总质量为m=75 kg,以初速度v0=8 m/s沿倾角为θ=37°的斜坡向上自由滑行,已知滑板与斜坡间动摩擦因数μ=0.25,假设斜坡足够长。不计空气阻力。试求:
(1)运动员沿斜坡上滑的最大距离;
(2)若运动员滑至最高点后掉转方向向下自由滑行,求他滑到起点时的速度大小。
解析:(1)上滑过程中,对人进行受力分析,滑雪者受重力mg、弹力FN、摩擦力f,并设滑雪者加速度为a1
根据牛顿第二定律有:
mgsinθ+f=ma1,a1方向沿斜面向下①
由平衡关系有:FN=mgcosθ②
根据动摩擦定律有:f=μFN③
由上列各式解得:a1=g(sinθ+μcosθ)=8 m/s2④
滑雪者沿斜面向上做匀减速直线运动,
减速到为零时的位移x==4 m⑤
即滑雪者上滑的最大距离为4 m。
(2)滑雪者沿斜面下滑时,滑雪者受到斜面的摩擦力沿斜面向上,
设加速度大小为a2,
根据牛顿第二定律有:
mgsinθ-f=ma2,a2方向沿斜面向下 ⑥
由平衡关系有:FN=mgcosθ ⑦
根据动摩擦定律有:f=μFN ⑧
由上列各式解得:a2=g(sinθ-μcosθ)=4 m/s2 ⑨
滑雪者沿斜面向下做初速度为零的匀加速直线运动,
滑到出发点的位移大小为x=4 m
则滑雪者再次滑到出发点时速度大小:v==4 m/s=5.7 m/s。⑩
答案:(1)4 m (2)5.7 m/s
18. (12分)质量为M的木楔倾角为θ(θ<),静止在水平面上,当将一质量为m的木块放在斜面上时正好匀速下滑。如果用与斜面成α角的力F拉着木块匀速上滑(木块匀速上滑过程木楔仍在水平面上静止),如图所示。
求:(1)木块匀速上滑时木楔受到水平面的摩擦力是多少?
(2)现改变力F的方向仍使木块匀速上滑,则F与斜面夹角多大时,拉力F最小,并求出此力最小值Fmin。
解析:木块放在斜面上恰好匀速下滑,受力分析则有沿斜面方向mgsinθ=μmgcosθ,即μ=tanθ
(1)木块匀速上滑时,木块处于平衡状态,斜面静止也是平衡状态,木块和斜面均平衡,可以把二者看做一个整体,受力分析如下:
水平方向受力平衡有f=Fcos(θ+α)
(2)对木块m受力分析如下,自身重力mg竖直向下,斜面支持力FN垂直斜面方向向上,摩擦力f沿斜面向下
因向上匀速,则有沿斜面方向Fcosα=mgsinθ+f ①
垂直斜面方向Fsinα+FN=mgcosα ②
f=μFN ③
整理得F===
当α=θ时,拉力F最小,最小值即Fmin=mgsin2θ。
答案:(1)f=Fcos(θ+α) (2)当α=θ时,拉力F最小,最小值即Fmin=mgsin2θ
(时间90分钟 满分100分)
一、选择题(本题共12小题,每小题4分,共48分。在每小题给出的四个选项中,第2、3、4、8、9、11小题,只有一个选项正确,第1、5、6、7、10、12小题,每题有多个选项正确,全部选对的得4分,选对而不全的得2分,错选或不选的得0分。)
1.[2014·山东莱芜一中高一期中]下列说法中正确的是( )
A.伽利略的理想实验说明物体的运动不需要力来维持
B. 牛顿第一定律说明力是改变物体运动状态的原因
C.同一汽车,速度越快,越难刹车,说明物体速度越大,惯性越大
D.已知月球上的重力加速度是地球上的,故一个物体从地球移到月球惯性减小为
解析:惯性是物体的一种属性,不随v变化,与质量有关,C、D错。
答案:AB
2. 下面是摘自上个世纪美国报纸上的一篇文章:阿波罗登月火箭在脱离地球飞向月球的过程中,宇航员通过无线电与在家中上小学的儿子汤姆通话。宇航员:“汤姆,我们现在已关闭了火箭上所有的发动机,正向月球飞去。”汤姆:“你们关闭了所有的发动机,那么靠什么力量推动火箭向前运动呢?”宇航员犹豫了半天,说:“我想大概是伽利略在推动火箭向前运动吧。”若不计天体对火箭的引力,由上述材料可知下列说法错误的是( )
A.汤姆问话所体现的物理思想是“力是维持物体运动的原因”
B. 宇航员答话所体现的物理思想是“力是维持物体运动的原因”
C.宇航员答话所体现的物理思想是“物体运动不需要力来维持”
D.宇航员答话的真实意思是火箭正在依靠惯性飞行
解析:汤姆问“靠什么力量推动火箭向前运动?”说明汤姆认为火箭向前运动必须有力的作用,即力是维持物体运动的原因,A正确。宇航员的回答提出伽利略,而伽利略的观点是力不是维持物体运动状态的原因,而是改变物体运动状态的原因,即运动不需要力来维持,物体具有保持原来运动状态的性质即惯性,答案C、D对。答案B错。
答案:B
3. 惯性制导系统已广泛应用于弹道式导弹工程中,这个系统的重要元件之一是加速度计。加速度计的构造原理的示意图如右图所示:沿导弹长度方向安装的固定光滑杆上套一质量为m的滑块,滑块两侧分别与劲度系数为k的弹簧相连;两弹簧的另一端与固定壁相连。滑块原来静止,弹簧处于自然长度。滑块上有指针,可通过标尺测出滑块的位移,然后通过控制系统进行制导。设某段时间内导弹沿水平方向运动,指针向左偏离O点的距离为x,则这段时间内导弹的加速度( )
A.方向向左,大小为kx/m B.方向向右,大小为kx/m
C.方向向左,大小为2kx/m D.方向向右,大小为2kx/m
解析:原来弹簧处于自然长度,后来指针向左偏离O点距离x,则左边弹簧压缩x,右边弹簧伸长x,滑块受的合力为2kx,方向向右。由牛顿第二定律:2kx=ma,加速度a=2kx/m,方向向右。
答案:D
4. [2014·杭州二中高一期中]“神舟九号”飞船与“天宫一号”空间站在太空中成功对接后稳定运行在预定的轨道上,其内部平台上的一台实验仪器处于失重状态,这时( )
A.如仪器是天平的话,就不能使用
B. 平台对仪器的弹力不为零
C.如仪器是弹簧秤的话,就不能使用
D.以上说法都不对
解析:处于完全失重状态,物体间接触但无力的作用,A对,B错。弹簧秤可测拉力,不能测物体的重力,C错。
答案:A
5. [2014·山西大学附中高一考试]气球吊着两个质量相同的重物A、B以10 m/s的速度匀速上升,两个重物之间用轻弹簧连接,重力加速度为g,若在距离地面上方10 m处绳子突然断裂,在断开瞬间有( )
A.vA=0 B.vB=10 m/s
C.aA=g D.aB=0
解析:设每个物体质量均为m,匀速上升时,绳上拉力FT=2mg,弹簧的弹力F=mg。绳子突然断裂的瞬间,两物体的速度没有改变,均为10 m/s,选项A错误、B正确;绳子的拉力消失,弹簧弹力没有变化,对A:F+mg=maA,得aA=2g,对B:因F=mg,故aB=0,选项C错误、D正确。
答案:BD
6. 如右图所示,有一物体从静止开始自有一定倾角的斜面顶点无摩擦往下滑动,下图中哪个图象能正确表示物体的加速度、速度的x分量随时间变化的关系( )
解析:设斜面的倾角为θ,物体的加速度为a=gsinθ,其水平分量为ax=gsinθcosθ,不变,故选项A错、B对;物体的水平分速度vx=axt,vx与t成正比,故选项C对、D错。
答案:BC
7. 斜面上的物体受到平行于斜面向下的力F作用,力F随时间变化的F-t图象及物体运动的v-t图象如图所示。由图象中的信息能够求出的量或可以确定的关系是( )
A.物体的质量m B. 斜面的倾角θ
C.物体与斜面间的动摩擦因数μ D.μ>tanθ
解析:由图象可以看出,拉力为F1=2 N时,物体匀速运动,拉力F2=3 N时,加速度为1 m/s2,所以有F1+mgsinθ-μmgcosθ=0①
F2+mgsinθ-μmgcosθ=ma②
两式相减可得F2-F1=ma,m=1 kg。
θ和μ不能求出,但由①可知,μ>tanθ。
答案:AD
8. 如图所示,在倾角为θ的固定光滑斜面上,质量为m的物体受外力F1和F2的作用,F1方向水平向右,F2方向竖直向上。若物体静止在斜面上,则下列关系正确的是( )
A.F1sinθ+F2cosθ=mgsinθ,F2≤mg
B. F1cosθ+F2sinθ=mgsinθ,F2≤mg
C.F1sinθ-F2cosθ=mgsinθ,F2≤mg
D.F1cosθ-F2sinθ=mgsinθ,F2≤mg
解析:对斜面上物体受力分析如图,建立以沿斜面方向为x轴,垂直斜面方向为y轴的坐标系,物体静止在斜面上,由平衡条件可得:沿x方向的合力为0:F1cosθ+F2sinθ=mgsinθ
如果考虑竖直方向合力为0:F2+Ncosθ=mg,F2≤mg可见,选择B。
答案:B
9. 某中学实验小组的同学在电梯的天花板上固定一根弹簧测力计,使其测量挂钩(跟弹簧相连的挂钩)向下,并在钩上悬挂一个重为10 N的钩码。弹簧测力计弹力随时间变化的规律如图所示,根据F-t图象,下列分析正确的是( )
A.从时刻t1到t2,钩码处于超重状态
B. 从时刻t3到t4,钩码处于失重状态
C.电梯可能开始停在15楼,先加速向下,接着匀速向下,再减速向下,最后停在1楼
D.电梯可能开始停在1楼,先加速向上,接着匀速向上,再减速向上,最后停在15楼
解析:0~t1阶段,物体处于平衡(静止或匀速)状态;t1~t2阶段,物体处于失重(加速下降或减速上升)状态;t2~t3阶段,物体处于平衡状态;t3~t4阶段,物体处于超重(加速上升或减速下降)状态,选项C正确。
答案:C
10. 一枚火箭由地面竖直向上发射,其速度和时间的关系图线如图所示,则( )
A.t3时刻火箭距地面最远
B.t2~t3的时间内,火箭在向下降落
C.t1~t2的时间内,火箭处于超重状态
D.0~t3的时间内,火箭始终处于失重状态
解析:本题考查对v-t图象的理解、超重、失重,分析时要由图象结合速度正负的意义、加速度正负的意义进行分析。速度始终为正值,说明火箭始终是向上运动的,故t3时刻火箭距地面最远,A选项正确,B选项错误;0~t2时间内,火箭加速上升,加速度向上,处于超重状态,t2~t3时间内火箭减速上升,加速度向下,处于失重状态,C选项正确,D选项错误。
答案:AC
11. 如右图所示,静止的倾斜传送带上有一木块正在匀速下滑,当传送带突然向上开动后,下列说法正确的是( )
A.木块所受摩擦力变大
B. 木块到底部所走位移变大
C.木块到底部所用时间变长
D.木块到底部所用的时间不变
解析:传送带静止和向上开动,两种情况下,物体受的滑动摩擦力的大小和方向都是相同的。所以物体的运动情况相同。到达底部所用的时间不变。
答案:D
12. 如图甲所示,某人正通过定滑轮将质量为m的货物提升到高处。滑轮的质量和摩擦均不计,货物获得的加速度a与绳子对货物竖直向上的拉力FT之间的函数关系如图乙所示。由图可以判断( )
A.图线与纵轴的交点M的值aM=-g
B. 图线与横轴的交点N的值FTN=mg
C.图线的斜率等于物体的质量m
D.图线的斜率等于物体质量的倒数
解析:由牛顿第二定律,有FT-mg=ma,故得a=-g,当FT=0时,a=-g,选项A正确;当a=0时,FT=mg,选项B正确;图线的斜率k=,选项D正确。
答案:ABD
二、填空题(本题共2小题,每小题5分,共10分。)
13. 依据“验证平行四边形定则”的实验,回答下列问题:
(1)在该实验中,合力与分力的概念是一种________的科学思想方法。
(2)某同学在做该实验时,弹簧测力计平行于木板如图放置,然后记录力的大小和方向,请你指出这样操作的问题:________________________________________。
解析:(1)等效替代
(2)弹簧测力计的轴线与细线套不在同一直线上,导致测量数据不准确。
答案:见解析
14. 在保持质量不变,探究加速度与物体受力间关系的实验中(使用教材提供的装置),小车质量M和砝码质量m分别选取下列四组值:
A.M=500 g,m分别为50 g、70 g、100 g、125 g
B.M=500 g,m分别为20 g、30 g、40 g、50 g
C.M=200 g,m分别为50 g、75 g、100 g、125 g
D.M=200 g,m分别为30 g、40 g、50 g、60 g
(1)如果其他操作都正确,那么在选用________组值测量时所画出的图线较准确。
(2)在选用此组值时,m取________时实验误差较大。
解析:在B组数据中,最容易满足小车质量M远大于砝码质量m的条件。
答案:(1)B (2)50 g
三、计算题(本题共4小题,共42分。要有必要的文字说明和演算步骤。有数值计算的题注明单位。)
15. (10分)[2014·南阳市五校联考高一期中]如图所示,一重为200 N的物体静止于水平地面上,若用一劲度系数为20 N/cm的轻质弹簧水平拉此物体,当弹簧的伸长量为4 cm时,物体恰在水平面上做匀速直线运动。求:
(1)弹簧弹力的大小;
(2)物体与水平面间的动摩擦因数。
解析:(1)由F=kx得
F=kx=20×102×4×10-2 N=80 N。
(2)由题意可知,物体匀速运动,弹簧的拉力与摩擦力相等,所以F=f
又∵f=μFN=μG
∴μ=0.4。
答案:(1)80 N (2)0.4
16. (10分)科研人员乘气球进行科学考察,气球、座舱、压舱物和科研人员的总质量为990 kg。气球在空中停留一段时间后,发现气球漏气而下降,及时堵住。堵住时气球下降速度为1 m/s,且做匀加速运动,4 s内下降了12 m。为使气球安全着陆,向舱外缓慢抛出一定的压舱物。此后发现气球做匀减速运动,下降速度在5分钟内减少了3 m/s。若空气阻力和泄漏气体的质量均可忽略,重力加速度g取9.89 m/s2,求抛掉的压舱物的质量。
解析:设堵住漏洞后,气球的初速度为v0,所受的空气浮力为f,气球、座舱、压舱物和科研人员的总质量为m,由牛顿第二定律得mg-f=ma ①
式中a是气球下降的加速度,以此加速度在时间t内下降了h,则
h=v0t+at2 ②
当向舱外抛掉质量为m′的压舱物后,有
f-(m-m′)g=(m-m′)a′ ③
式中a′是抛掉压舱物后气球的加速度,由题意,此时a′方向向上
Δv=a′Δt ④
式中Δv是抛掉压舱物后在Δt时间内下降速度的减少量。由①③得
m′=m ⑤
将题设数据
m=990 kg,v0=1 m/s,t=4 s,h=12 m,Δt=300 s,
Δv=3 m/s,g=9.89 m/s2
代入②④⑤式得m′=101 kg。 ⑥
答案:101 kg
17. (10分)如图所示,一个滑雪运动员,滑板和人总质量为m=75 kg,以初速度v0=8 m/s沿倾角为θ=37°的斜坡向上自由滑行,已知滑板与斜坡间动摩擦因数μ=0.25,假设斜坡足够长。不计空气阻力。试求:
(1)运动员沿斜坡上滑的最大距离;
(2)若运动员滑至最高点后掉转方向向下自由滑行,求他滑到起点时的速度大小。
解析:(1)上滑过程中,对人进行受力分析,滑雪者受重力mg、弹力FN、摩擦力f,并设滑雪者加速度为a1
根据牛顿第二定律有:
mgsinθ+f=ma1,a1方向沿斜面向下①
由平衡关系有:FN=mgcosθ②
根据动摩擦定律有:f=μFN③
由上列各式解得:a1=g(sinθ+μcosθ)=8 m/s2④
滑雪者沿斜面向上做匀减速直线运动,
减速到为零时的位移x==4 m⑤
即滑雪者上滑的最大距离为4 m。
(2)滑雪者沿斜面下滑时,滑雪者受到斜面的摩擦力沿斜面向上,
设加速度大小为a2,
根据牛顿第二定律有:
mgsinθ-f=ma2,a2方向沿斜面向下 ⑥
由平衡关系有:FN=mgcosθ ⑦
根据动摩擦定律有:f=μFN ⑧
由上列各式解得:a2=g(sinθ-μcosθ)=4 m/s2 ⑨
滑雪者沿斜面向下做初速度为零的匀加速直线运动,
滑到出发点的位移大小为x=4 m
则滑雪者再次滑到出发点时速度大小:v==4 m/s=5.7 m/s。⑩
答案:(1)4 m (2)5.7 m/s
18. (12分)质量为M的木楔倾角为θ(θ<),静止在水平面上,当将一质量为m的木块放在斜面上时正好匀速下滑。如果用与斜面成α角的力F拉着木块匀速上滑(木块匀速上滑过程木楔仍在水平面上静止),如图所示。
求:(1)木块匀速上滑时木楔受到水平面的摩擦力是多少?
(2)现改变力F的方向仍使木块匀速上滑,则F与斜面夹角多大时,拉力F最小,并求出此力最小值Fmin。
解析:木块放在斜面上恰好匀速下滑,受力分析则有沿斜面方向mgsinθ=μmgcosθ,即μ=tanθ
(1)木块匀速上滑时,木块处于平衡状态,斜面静止也是平衡状态,木块和斜面均平衡,可以把二者看做一个整体,受力分析如下:
水平方向受力平衡有f=Fcos(θ+α)
(2)对木块m受力分析如下,自身重力mg竖直向下,斜面支持力FN垂直斜面方向向上,摩擦力f沿斜面向下
因向上匀速,则有沿斜面方向Fcosα=mgsinθ+f ①
垂直斜面方向Fsinα+FN=mgcosα ②
f=μFN ③
整理得F===
当α=θ时,拉力F最小,最小值即Fmin=mgsin2θ。
答案:(1)f=Fcos(θ+α) (2)当α=θ时,拉力F最小,最小值即Fmin=mgsin2θ
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
