绝对值
图片预览







文档简介
(共22张PPT)
不同的 个数叫做互为相反数.
只有符号
两
求一个数的相反数,只需 即可.
在其前面加上“—”号
即a的相反数是 ,
-a
0的相反数是 .
0
在数轴上表示相反数(0除外)的两个点位于原点的 ,且与原点的距离 .
两侧
相等
※多重符号的化简方法:
“数数负号,偶正奇负.”
找规律:观察下列次序排列的一列数,你能发现它们排列的规律吗?请写出它后面的两个数.
(1)1,-2,3,-4, , ;
5
-6
(2) , , , , , .
2
1
3
2
4
3
5
4
6
5
7
6
[09湖北模拟]数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8,…观察并猜想第六个数是 .
65
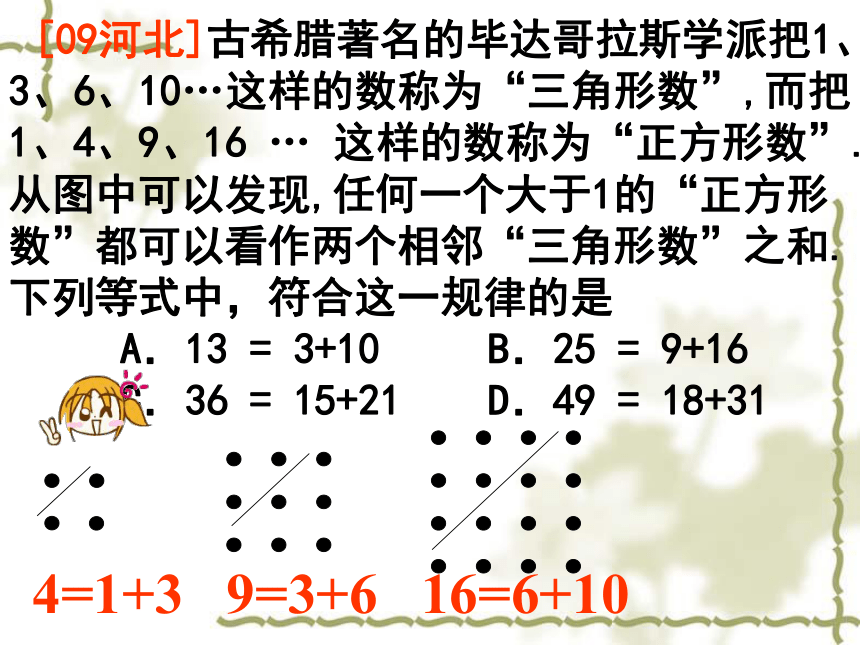
[09河北]古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是
A.13 = 3+10 B.25 = 9+16
C.36 = 15+21 D.49 = 18+31
4=1+3 9=3+6 16=6+10
引入:两辆汽车从同一处O出发分别向、东、西方向行驶10km,到达A、B两处.
0
10
B
-10
A
10
10
(1)它们的行驶路线的方向相同吗
(2)它们行驶路程的距离(线段OA、OB的长度)相同吗
O
不同
相同
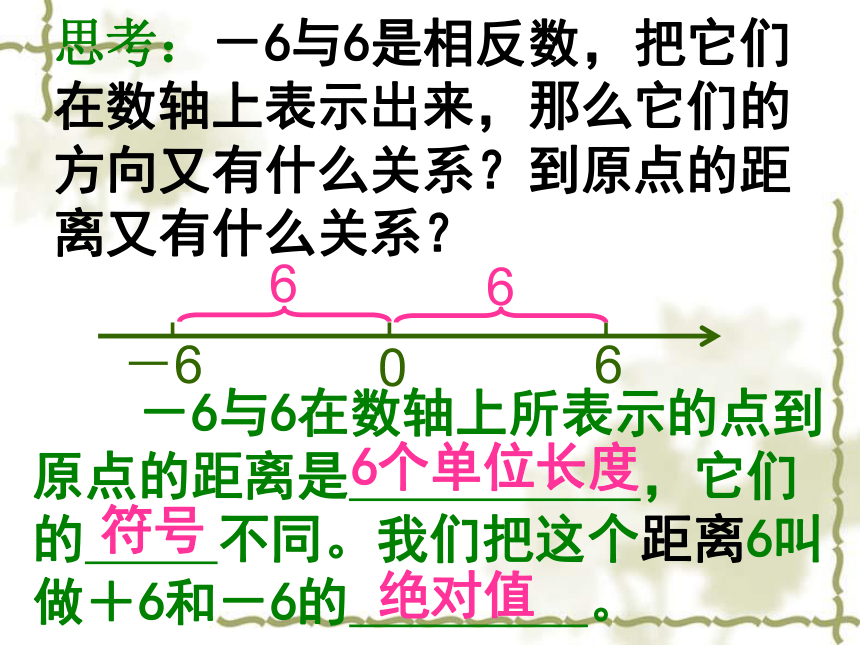
思考:-6与6是相反数,把它们在数轴上表示出来,那么它们的方向又有什么关系?到原点的距离又有什么关系?
-6与6在数轴上所表示的点到原点的距离是 ,它们的 不同。我们把这个距离6叫做+6和-6的 。
-6
6
0
6
6
6个单位长度
符号
绝对值
一般地,数轴上表示数a的点与 叫做数a的绝对值,记作: .
想一想,互为相反数的两个数的绝对值有什么关系?
一.绝对值的几何意义
原点的距离
互为相反数的两个数的绝对值 .
|a|
相等
练习:
(1)绝对值是3的数有几个 各是什么
(2)绝对值是0的数有几个 各是什么
(3)绝对值是-2的数是否存在?
若存在,请说出来?
绝对值是3的数有两个,
它们分别是+3,-3.
绝对值是0的数只有一个0.
不存在绝对值是-2的数.
例如:
| -7 | =
| 10 | =
求10,-7,0的绝对值?
解:
10,
7,
| 0 | =
0.
练习:求下列各数的绝对值。
-19, ,0,-2.3,+0.56,
3
2
-2,6, .
4
1
2
| -19 | =
19,
3
2
=
3
2
,
| 0 | =
0,
思考:上述各数的绝对值与这些数本身有什么关系?
负数
1.一个数的绝对值不可能为 ;
※二.绝对值的性质
2.一个正数的绝对值是 ;
它本身
一个负数的绝对值是 ;
零的绝对值是 ;
它的相反数
0
的范围?
≥0
化简:
(1)|-0.1|=____; (2)|-101|=____;
(3)| |=______;(4)|-6|=_____;
(5)|y|=____=(y<0);(6)| |=_____;
(7)-|-7.5|=_____; (8)-|+8|=____;
(9)如果|x|=2,则x=______;
(10)如果|x-3|=0,则|x+2|= .
0.1
101
6
-y
-7.5
-8
±2
5
※三.有理数的大小比较
1.正数 0, 0 负数,
正数 负数;
大于
0
1
2
3
-1
-2
-3
大于
大于
例如:教材13
1 0, 0 -1, 1 -1, -1 -2.
>
>
>
>
思考:两个负数如何比较大小?
※2.两个负数,绝对值大的 .
反而小
0
1
2
3
-1
-2
-3
例如:比较下列各数的大小
(1) –(-1)和–(+2);
解:
–(-1)=
1,
–(+2)=
-2,
∵ 1>-2
∴–(-1)>–(+2).
(2) 和 ;
21
8
7
3
解:
21
8
=
7
3
=
21
8
7
3
=
21
9
21
8
∵
21
9
<
21
8
∴
7
3
>
(3) -(-0.3)和 ;
3
1
解:
-(-0.3)=
0.3,
3
1
=
3
1
∵ 0.3<
3
1
∴ -(-0.3)< .
3
1
练习:判断对错
(1)|-1.4|>0 ( )
(2)|-0.3|=|0.3| ( )
(3)有理数的绝对值一定是正数.( )
(4)绝对值最小的数是0。( )
(5)如果数a的绝对值等于a,
那么a一定为正数。( )
×
√
√
√
×
(6)符号相反且绝对值相等的数互为相反数。( )
(7)一个数的绝对值越大,表示它的点在数轴上越靠右。( )
(8)一个数的绝对值越大,表示它的点在数轴上离原点越远 ( )
(9)若a=b,则|a|=|b|( )
(10)若|a|=|b|,则a=b.( )
√
×
×
√
√
不同的 个数叫做互为相反数.
只有符号
两
求一个数的相反数,只需 即可.
在其前面加上“—”号
即a的相反数是 ,
-a
0的相反数是 .
0
在数轴上表示相反数(0除外)的两个点位于原点的 ,且与原点的距离 .
两侧
相等
※多重符号的化简方法:
“数数负号,偶正奇负.”
找规律:观察下列次序排列的一列数,你能发现它们排列的规律吗?请写出它后面的两个数.
(1)1,-2,3,-4, , ;
5
-6
(2) , , , , , .
2
1
3
2
4
3
5
4
6
5
7
6
[09湖北模拟]数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8,…观察并猜想第六个数是 .
65
[09河北]古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是
A.13 = 3+10 B.25 = 9+16
C.36 = 15+21 D.49 = 18+31
4=1+3 9=3+6 16=6+10
引入:两辆汽车从同一处O出发分别向、东、西方向行驶10km,到达A、B两处.
0
10
B
-10
A
10
10
(1)它们的行驶路线的方向相同吗
(2)它们行驶路程的距离(线段OA、OB的长度)相同吗
O
不同
相同
思考:-6与6是相反数,把它们在数轴上表示出来,那么它们的方向又有什么关系?到原点的距离又有什么关系?
-6与6在数轴上所表示的点到原点的距离是 ,它们的 不同。我们把这个距离6叫做+6和-6的 。
-6
6
0
6
6
6个单位长度
符号
绝对值
一般地,数轴上表示数a的点与 叫做数a的绝对值,记作: .
想一想,互为相反数的两个数的绝对值有什么关系?
一.绝对值的几何意义
原点的距离
互为相反数的两个数的绝对值 .
|a|
相等
练习:
(1)绝对值是3的数有几个 各是什么
(2)绝对值是0的数有几个 各是什么
(3)绝对值是-2的数是否存在?
若存在,请说出来?
绝对值是3的数有两个,
它们分别是+3,-3.
绝对值是0的数只有一个0.
不存在绝对值是-2的数.
例如:
| -7 | =
| 10 | =
求10,-7,0的绝对值?
解:
10,
7,
| 0 | =
0.
练习:求下列各数的绝对值。
-19, ,0,-2.3,+0.56,
3
2
-2,6, .
4
1
2
| -19 | =
19,
3
2
=
3
2
,
| 0 | =
0,
思考:上述各数的绝对值与这些数本身有什么关系?
负数
1.一个数的绝对值不可能为 ;
※二.绝对值的性质
2.一个正数的绝对值是 ;
它本身
一个负数的绝对值是 ;
零的绝对值是 ;
它的相反数
0
的范围?
≥0
化简:
(1)|-0.1|=____; (2)|-101|=____;
(3)| |=______;(4)|-6|=_____;
(5)|y|=____=(y<0);(6)| |=_____;
(7)-|-7.5|=_____; (8)-|+8|=____;
(9)如果|x|=2,则x=______;
(10)如果|x-3|=0,则|x+2|= .
0.1
101
6
-y
-7.5
-8
±2
5
※三.有理数的大小比较
1.正数 0, 0 负数,
正数 负数;
大于
0
1
2
3
-1
-2
-3
大于
大于
例如:教材13
1 0, 0 -1, 1 -1, -1 -2.
>
>
>
>
思考:两个负数如何比较大小?
※2.两个负数,绝对值大的 .
反而小
0
1
2
3
-1
-2
-3
例如:比较下列各数的大小
(1) –(-1)和–(+2);
解:
–(-1)=
1,
–(+2)=
-2,
∵ 1>-2
∴–(-1)>–(+2).
(2) 和 ;
21
8
7
3
解:
21
8
=
7
3
=
21
8
7
3
=
21
9
21
8
∵
21
9
<
21
8
∴
7
3
>
(3) -(-0.3)和 ;
3
1
解:
-(-0.3)=
0.3,
3
1
=
3
1
∵ 0.3<
3
1
∴ -(-0.3)< .
3
1
练习:判断对错
(1)|-1.4|>0 ( )
(2)|-0.3|=|0.3| ( )
(3)有理数的绝对值一定是正数.( )
(4)绝对值最小的数是0。( )
(5)如果数a的绝对值等于a,
那么a一定为正数。( )
×
√
√
√
×
(6)符号相反且绝对值相等的数互为相反数。( )
(7)一个数的绝对值越大,表示它的点在数轴上越靠右。( )
(8)一个数的绝对值越大,表示它的点在数轴上离原点越远 ( )
(9)若a=b,则|a|=|b|( )
(10)若|a|=|b|,则a=b.( )
√
×
×
√
√
