全等三角形

(共30张PPT)
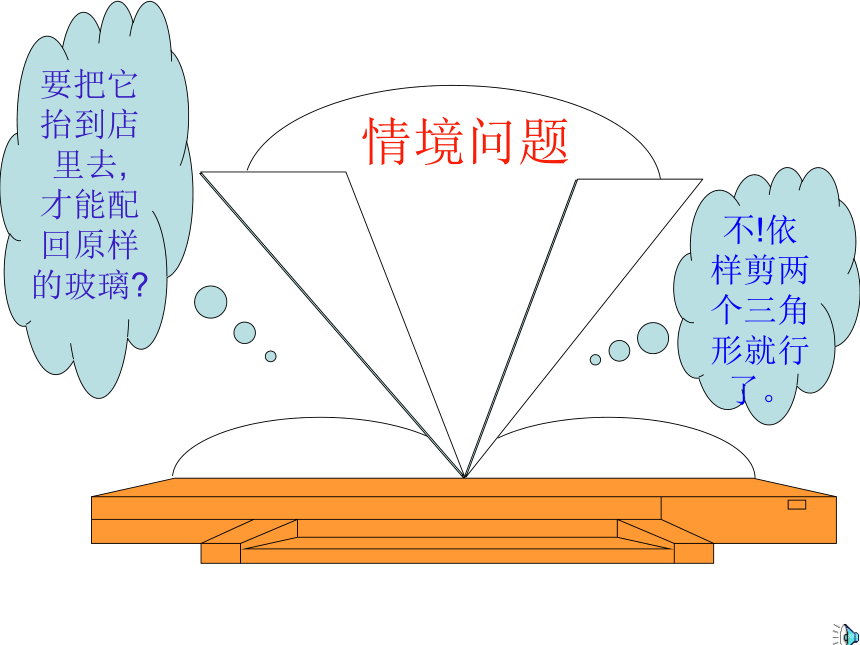
要把它抬到店里去,才能配回原样的玻璃
情境问题
不!依样剪两个三角形就行了。
同一张底片洗出的同尺寸的照片是能够完全重合的
说一说
你能举出生活中的一些实际例子吗？
找一找
这几张图片里都有形状、大小相同的图形。比一比：谁找得多？
两张纸重合 后 剪纸，得到的两个图形 大 小、形状相同。
说一说
说一说
电脑复制的图形大小、形状也相同
说一说
平移、翻折、旋转形状、大小都不变
结论：平移、翻折、旋转前后的图形全等。
1.平移
2.翻折
3.旋转
拼一拼
做一做
将一块三角形样板按在纸板上,画下图形,照样裁下纸板。
比一比： 裁下的纸板和样板的形状、大小是否 完 全 一样？能 完全重合吗？
能够完全重合的两个图形；
全 等 形：
全等三角形：
定 义
能够完全重合的两个三角形。
A
B
C
D
F
E
A
B
C
把两个全等的三角形重合在一起
●重合的顶点叫对应顶点
●重合的边叫对应边
●重合的角叫对应角
D
F
E
注意：表示时通常把对应顶点的字母写在对应的位置上。
△ABC △DEF
≌
△ABC全等于△DEF可表示为：
（“≌”读作“全等于”）
你能否直接从记作 ABC≌ DEF中判断出所有的对应顶点、对应边和对应角？
A
C
B
F
E
D
想一想
能否记作 ABC≌ DEF
应该记作 ABC≌ DFE
原因:A与D、B与F、C与E对应。
A
D
B
C
E
F
≌
试一试： 根据图形所提供的条件和全等式：
（1）在图上标出所缺的字母；
（2）说出它们的对应边和对应角
A
B
C
D
E
F
先写出全等式，再指出它们的
对应边和对应角
试一试1：
≌
先写出全等式，再指出它们的
对应边和对应角
试一试2：
A
C
O
D
B
≌
D
A
C
B
先写出全等式，再指出它们的
对应边和对应角
试一试3：
≌
A
B
C
D
先写出全等式，再指出它们的
对应边和对应角
试一试4：
≌
活学活用
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
将剪得的两个全等三角形，按下列位置摆一摆；并指出它们的对应点、对应边、对应角。
全等对应元素的找法
寻找对应元素的规律
（1）有公共边的，公共边是对应边；
（2）有公共角的，公共角是对应角；
（3）有对顶角的，对顶角是对应角；
（4）两个全等三角形最大的边是对应边，最小的边也是对应边；
（5）两个全等三角形最大的角是对应角，最小的角也是对应角；
（1）怎样的两条线段叫对应边？
（2）互相重合的两条线段的大小情况怎样？
可见，全等三角形的对应边相等
同理，全等三角形能够互相重合的两角是对应角，而能互相重合的两角大小是相等的。
所以，全等三角形的对应角相等
如图： ∵ △ABC≌△DEF
全等三角形的性质： 对应边相等，对应角相等
∴A B=D E，A C=D F，BC= E F
∠A=∠D，∠B=∠E，∠C=∠F
（全等三角形的对应边相等）
（全等三角形的对应角相等）
填一填
角
角
角
边
边
边
AC=BD
MC=MD
AM=BM
∠A=∠B
∠C=∠D
∠AMC=∠BMD
△＿＿＿≌△＿＿＿
AMC
BMD
图中能用字母表示
的全等三角形是：
（较短的）
（较长的）
（较小的）
（较大的）
A
B
C
D
E
O
活学活用
△ABD≌△ACE，若∠B＝25°，BD＝6㎝，AD＝4㎝，你能得出△ACE中哪些角的大小，哪些边的长度吗？为什么 ？
全等性质的运用
课外作业：Ｐ4－1、2、3、4　　　　　　　　　　　
重点掌握：
明白道理：
“全等”和“对应相等”
因“完全重合”而“全等”
因“完全重合”而“对应”边(角)相等
口 诀：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　形状相同大小等，完全重合是根本；
顶点一二三对应，边角相等方入门。