角的平分线性质 说课
图片预览


文档简介
(共25张PPT)
第 一 课 时
角的平分线的性质
说课内容
一.说 教 材
地位作用
学情分析
重点难点
教学目标
本节课主要学习了角平分线的作法,角平分线的性质及其应用,是在学生学习了角平分线的概念和三角形全等的基础上引入的.
八年级学生已经具备了初步归纳的能力,但是他们全面深入探究问题能力较弱,他们对问题的认识主要依赖于感性认识.
知识目标:1.掌握角平分线的作法
2.理解角平分线的性质
3.运用角平分线的性质
能力目标:培养学生动手实践,演绎
推理的能力.
情感目标:激发学生学习兴趣,增强
学生学好数学的信心.
重点:1.角平分线的画法
2.角平分线性质的应用
难点:探究角平分线的性质
关键:通过情景问题的设计,引导学生
发现、分析和解决问题.
地位作用
学情分析
重点难点
二.说 教 法
激发学生的学习动机,提高学生的学习兴趣.
启发学生探究角平分线的
性质.
使教学内容更加直观,提高整个课堂的教学效果.
教学方法
情景教学
启发教学
直观演示
培养学生自学能力
课堂
讨论
动手
实践
观察
发现
三.说 学 法
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
角平分线的定义是什么 如何作出角平分线呢
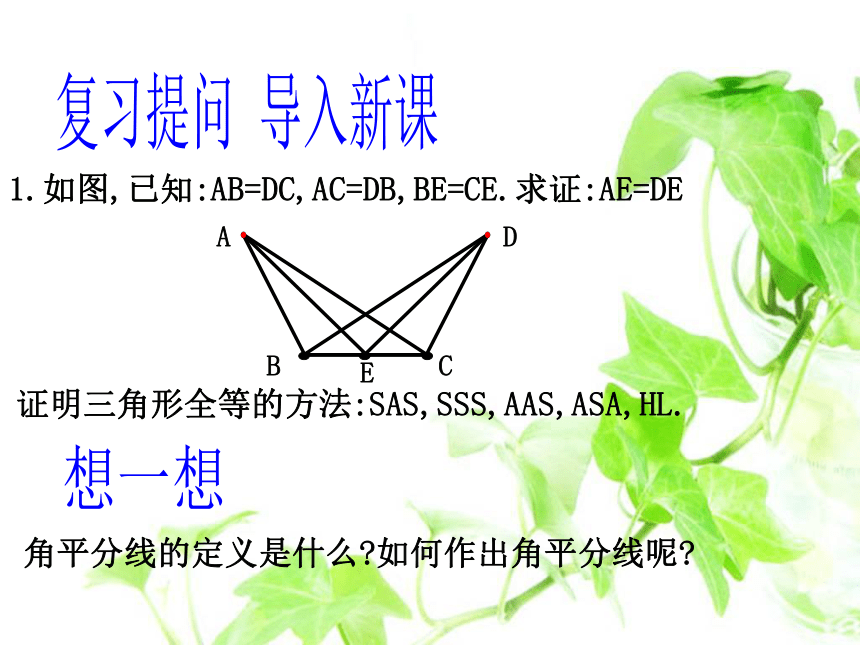
1.如图,已知:AB=DC,AC=DB,BE=CE.求证:AE=DE
证明三角形全等的方法:SAS,SSS,AAS,ASA,HL.
A
B
C
D
E
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
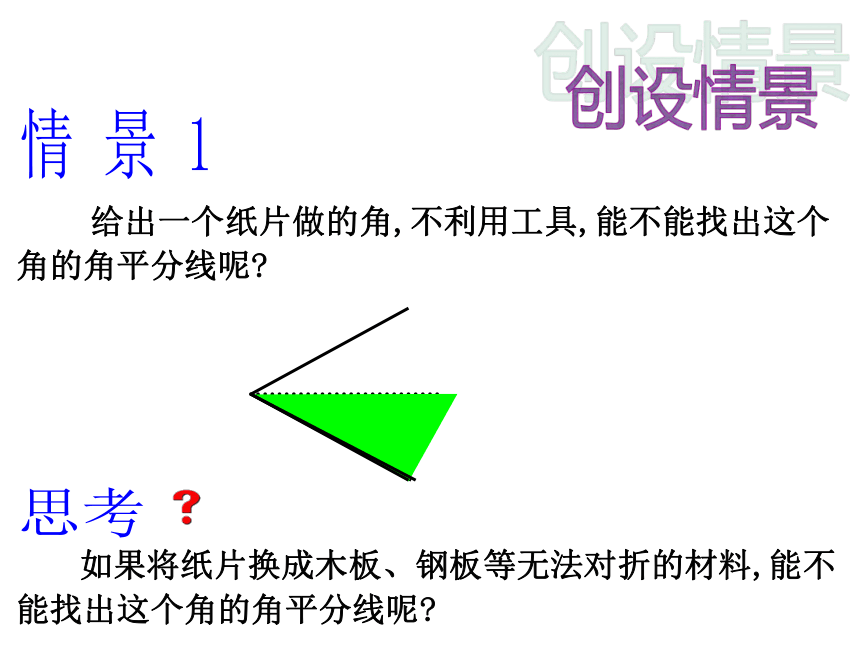
给出一个纸片做的角,不利用工具,能不能找出这个角的角平分线呢
如果将纸片换成木板、钢板等无法对折的材料,能不能找出这个角的角平分线呢
如图,是一个木匠用的角平分仪,其中AB=AD,BC=DC.沿AC画一条射线AE.AE就是∠BAD的角平分线,你能说明它的道理吗
根据角平分仪的制作原理你能作出∠EOF的角平分线吗?
分析:要证角相等
证明三角形全等
证明△ADC≌△ABC
C
B
E
A
D
O
E
F
C
B
A
D
C
E
N
M
如何在∠EOF内做出两个全等三角形呢?
作法:
1.以O为圆心,适当长为半径作弧,交
OE于点N,交OF于点M.
2.分别以M,N为圆心,大于MN一半的
长为半径作弧,两弧在∠EOF的内
部交于点C.
3.作射线OC.
将∠AOB对折,在折痕上任取一点P,过P点再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
P
A
O
B
C
E
D
角的平分线的性质:角的平分线上的点到角两边的距离相等
结论:PO为∠AOB的角平分线,PD⊥OA,
PE⊥OB,且PD=PE.
猜想:角的平分线上的点到角两边的
距离相等.
已知:如图,OC平分∠AOB,任意点P在OC上,PD⊥OA于点D,PE⊥
OB于点E.
求证:PD=PE.
分析:证明线段相等 证明三角形全等 证明
△ODP≌△OEP.
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
C
例1.尺规作图,做下列角的角平分线.
A
B
O
C
C
A
O
B
B
O
A
证明:过点P作PD,PE,PF分别垂直于AB,BC,AC
于D,E,F.
∵ BM是△ABC的角平分线,
点P在BM上,
∴ PD=PE. 同理 PE=PF.
∴ PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
A
N
B
C
M
P
例2.如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
D
E
∟
∟
∟
F
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
1.如图,E是∠AOB的角平分线OC上的一点,EM⊥OB垂足为M,
且EM=3cm,求点E到OA的距离.
合作交流 巩固提高
2.已知:如图,在△ABC中,AD是它的角平分线,且 BD=CD,
DE⊥AB,DF⊥AC垂足分别是E,F.
求证:EB=FC.
A
B
C
D
E
F
O
B
A
M
E
∟
(1题图)
∟
∟
(2题图)
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
1.如何做一个已知角的角平分线
2.角平分线的性质是什么
3.你会用角平分线的性质证明线段相等吗
必做题:P110 T1 T2
开放题:如图所示,AC,BC是公园的两道垂直的围墙,AD
是公园里的一排树,AB是一条路,AD正好平分∠BAC,并且BC=10m,BD=6m,工作人员想从D点修一条路到达AB所在的路上,那么怎么修最近,要修多少米?
C
A
B
D
板书设计
§13.3 角的平分线的性质
复习引入 角平分线的做法 例题讲解
情景猜想 角平分线的性质 课堂小结
第 一 课 时
角的平分线的性质
说课内容
一.说 教 材
地位作用
学情分析
重点难点
教学目标
本节课主要学习了角平分线的作法,角平分线的性质及其应用,是在学生学习了角平分线的概念和三角形全等的基础上引入的.
八年级学生已经具备了初步归纳的能力,但是他们全面深入探究问题能力较弱,他们对问题的认识主要依赖于感性认识.
知识目标:1.掌握角平分线的作法
2.理解角平分线的性质
3.运用角平分线的性质
能力目标:培养学生动手实践,演绎
推理的能力.
情感目标:激发学生学习兴趣,增强
学生学好数学的信心.
重点:1.角平分线的画法
2.角平分线性质的应用
难点:探究角平分线的性质
关键:通过情景问题的设计,引导学生
发现、分析和解决问题.
地位作用
学情分析
重点难点
二.说 教 法
激发学生的学习动机,提高学生的学习兴趣.
启发学生探究角平分线的
性质.
使教学内容更加直观,提高整个课堂的教学效果.
教学方法
情景教学
启发教学
直观演示
培养学生自学能力
课堂
讨论
动手
实践
观察
发现
三.说 学 法
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
角平分线的定义是什么 如何作出角平分线呢
1.如图,已知:AB=DC,AC=DB,BE=CE.求证:AE=DE
证明三角形全等的方法:SAS,SSS,AAS,ASA,HL.
A
B
C
D
E
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
给出一个纸片做的角,不利用工具,能不能找出这个角的角平分线呢
如果将纸片换成木板、钢板等无法对折的材料,能不能找出这个角的角平分线呢
如图,是一个木匠用的角平分仪,其中AB=AD,BC=DC.沿AC画一条射线AE.AE就是∠BAD的角平分线,你能说明它的道理吗
根据角平分仪的制作原理你能作出∠EOF的角平分线吗?
分析:要证角相等
证明三角形全等
证明△ADC≌△ABC
C
B
E
A
D
O
E
F
C
B
A
D
C
E
N
M
如何在∠EOF内做出两个全等三角形呢?
作法:
1.以O为圆心,适当长为半径作弧,交
OE于点N,交OF于点M.
2.分别以M,N为圆心,大于MN一半的
长为半径作弧,两弧在∠EOF的内
部交于点C.
3.作射线OC.
将∠AOB对折,在折痕上任取一点P,过P点再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
P
A
O
B
C
E
D
角的平分线的性质:角的平分线上的点到角两边的距离相等
结论:PO为∠AOB的角平分线,PD⊥OA,
PE⊥OB,且PD=PE.
猜想:角的平分线上的点到角两边的
距离相等.
已知:如图,OC平分∠AOB,任意点P在OC上,PD⊥OA于点D,PE⊥
OB于点E.
求证:PD=PE.
分析:证明线段相等 证明三角形全等 证明
△ODP≌△OEP.
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
C
例1.尺规作图,做下列角的角平分线.
A
B
O
C
C
A
O
B
B
O
A
证明:过点P作PD,PE,PF分别垂直于AB,BC,AC
于D,E,F.
∵ BM是△ABC的角平分线,
点P在BM上,
∴ PD=PE. 同理 PE=PF.
∴ PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
A
N
B
C
M
P
例2.如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
D
E
∟
∟
∟
F
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
1.如图,E是∠AOB的角平分线OC上的一点,EM⊥OB垂足为M,
且EM=3cm,求点E到OA的距离.
合作交流 巩固提高
2.已知:如图,在△ABC中,AD是它的角平分线,且 BD=CD,
DE⊥AB,DF⊥AC垂足分别是E,F.
求证:EB=FC.
A
B
C
D
E
F
O
B
A
M
E
∟
(1题图)
∟
∟
(2题图)
四.说教学过程
创
设
情
景
探
究
新
知
复
习
提
问
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
例
题
讲
解
形
成
技
能
1.如何做一个已知角的角平分线
2.角平分线的性质是什么
3.你会用角平分线的性质证明线段相等吗
必做题:P110 T1 T2
开放题:如图所示,AC,BC是公园的两道垂直的围墙,AD
是公园里的一排树,AB是一条路,AD正好平分∠BAC,并且BC=10m,BD=6m,工作人员想从D点修一条路到达AB所在的路上,那么怎么修最近,要修多少米?
C
A
B
D
板书设计
§13.3 角的平分线的性质
复习引入 角平分线的做法 例题讲解
情景猜想 角平分线的性质 课堂小结
