北师大版数学八年级上册2.1 认识无理数课件(第1课时 23张)
文档属性
| 名称 | 北师大版数学八年级上册2.1 认识无理数课件(第1课时 23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 881.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览







文档简介
2.1 认识无理数(第1课时)
已知一个直角三角形的两条直角边长分别为1和 2,算一算斜边长x的平方 ,x是整数(或分数)吗?
x2=?
1
2
x
导入新知
1.通过拼图活动和勾股定理的应用感受无理数产生的实际背景和引入的必要性.
2.能判断一个数是否为有理数.
素养目标
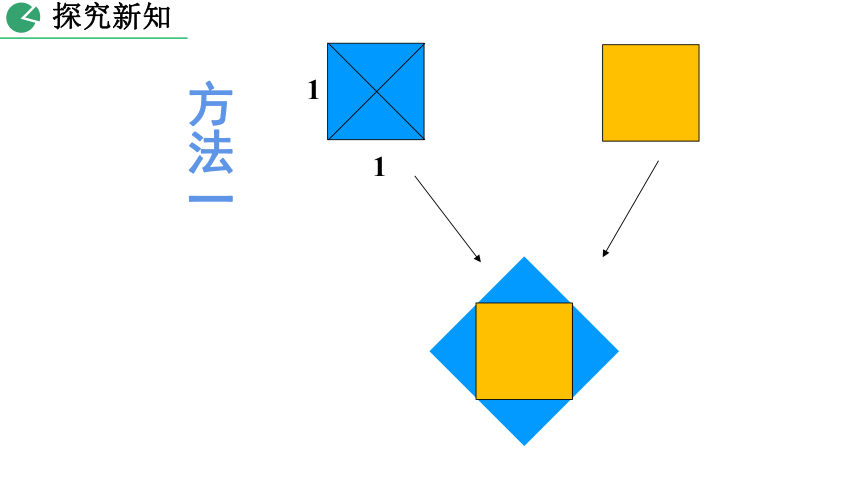
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形
剪一剪 拼一拼
1
1
1
1
探究一: 下面请同学们拿出准备好的两个边长为1的小正方形
探究新知
知识点 1
利用拼图发现非有理数
1
1
方法一
探究新知
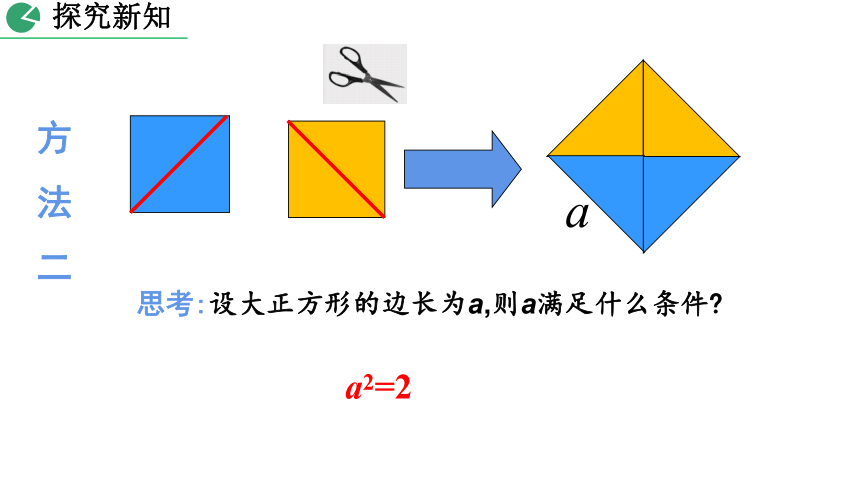
思考:设大正方形的边长为a,则a满足什么条件?
方
法
二
探究新知
a2=2
2.a可能是分数吗?说说你的理由.
探究二:
1.a可能是整数吗?说说你的理由.
探究新知
a2=2
a
因为a2=2,1所以a一定不是整数;
因为
所以a一定不是分数.
在等式a2=2中,a既不是整数,也不是分数,那么一定不是有理数.
探究新知
即两个相同最简分数的乘积仍是分数.
a2=2
a
归纳总结
有理数包括:整数和分数.
如果一个数既不是整数也不是分数,
那么这个数不是有理数.
在a2=2中,a不是有理数.
探究新知
例 如图,有一个由五个边长为1的小正方形组成的图形,我们可以把它剪拼成一个正方形.则拼成的正方形的面积是多少?这个正方形的边长是有理数吗?
解:因为小正方形的边长为1,
所以每个小正方形的面积为1,
所以拼成的正方形的面积为 5×1=5.
因为找不到平方等于5的有理数,
所以这个正方形的边长不是有理数.
探究新知
素养考点 1
非有理数的识别
提示:解决本题的关键是理解五个小正方形的面积的和就是拼成的正方形的面积.
1.满足下列条件的数a不是有理数的是 ( )
A.2a+5=8 B.a2=0.16
C.a2=7 D.a2=9
2.下列说法:①有理数都是有限小数;②有限小数都是有理数;③有理数都是无限循环小数;④无限循环小数都是有理数.其中正确的有 ( )
A.①② B.①③ C.②③ D.②④
C
D
巩固练习
变式训练
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,则b应满足什么条件?b是有理数吗?
解:b2=5.①因为22=4,32=9,4<5<9,
所以b不可能是整数.
②没有两个相同的分数相乘得5,故b不可能是分数.
③因为没有一个整数或分数的平方为5,所以b不是有理数.
探究新知
知识点 2
利用勾股定理发现非有理数
解:两条直角边分别为1和2,根据勾股定理,得12+22=5,所以正方形的面积是5.
像上面讨论的数a,b都不是有理数,而是另一类数—无理数.
早在公元前,古希腊数学家毕达哥拉斯认为万物皆“数”,即“宇宙间的一切现象都能归结为整数或整数之比”.但是这个学派中的一个叫希伯索斯的成员却发现边长为1的正方形的对角线的长不能用整数或整数之比来表示,这个发现动摇了毕达哥拉斯学派的信条,据说为此希伯索斯被投进了大海,他为真理而献出了宝贵的生命,但真理是不可战胜的,后来古希腊人终于正视了希伯索斯的发现.也就是a2=2中的a不是有理数.
探究新知
用生命换来的新数
归纳总结
例 如图,在△ABC中,CD⊥AB,垂足为D,AC=6,AD=5,问:CD可能是整数吗?可能是分数吗?可能是有理数吗?
解:在Rt△ACD中,AC为斜边,AC=6,AD=5,所以CD2=AC2-AD2=11.因为11是质数,大于1的整数的平方都是合数,所以11不能写成一个整数的平方,所以CD不可能是整数.
因为最简分数的平方仍是分数,所以CD不可能是分数.所以CD不可能是有理数.
素养考点 1
利用勾股定理识别非有理数
探究新知
如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
解:由正三角形的性质可知BD=1,在Rt△ABD中,
由勾股定理得h2=3.h不可能是整数,也不可能是分数.
巩固练习
变式训练
连接中考
D
(2020·威海模拟)下列正方形的边长不是有理数的是( )
A. 面积为2.56的正方形 B.面积为36的正方形
C.面积为 的正方形 D.面积为10的正方形
1 .满足下列条件的数不是有理数的是( )
课堂检测
基础巩固题
C
2.两直角边分别是3和5的直角三角形的斜边长是( )
A. 整数 B. 分数
C. 有理数 D.非有理数
D
C.a2=3
D.2a2=18
B. a2=0.36
A. 2a +5=8
D
2
不是
3.如果方程x2=m 的解是有理数,则数m不能取下列四个数中的( )
A. 1 B. 4 C. 0.25 D.0.5
4.把边长是1的两个正方形纸片重新剪裁成一个大的正方形,则大正方形的面积是______,它的边长_____有理数(填写“是”或“不是”)
课堂检测
基础巩固题
请你在方格纸上按照如下要求设计直角三角形.(所作三角形的各个顶点均在格点上)
(1)使它的一边为有理数,另两边边长不是有理数;
(2)使它的三边边长都是有理数.
能力提升题
课堂检测
解:(1)如图1所示.
(2)如图2所示.
图1
图2
能力提升题
课堂检测
在下列4×4的网格中,每个小正方形的边长都为1,请在每一个图中分别画出一条线段,且它们的长度均表示不等的非有理数.
拓广探索题
课堂检测
解:答案不唯一.如图所示:
AB2=2,2不能写成一个整数或分数的平方,所以AB表示的数是非有理数.
CD2=8,8不能写成一个整数或分数的平方,所以CD表示的数是非有理数.
EF2=18,18不能写成一个整数或分数的平方,所以EF表示的数是非有理数.
拓广探索题
课堂检测
非有理数的发现
拼图发现
首先通过拼图把几个小正方形拼成一个大正方形,然后利用面积发现非有理数
非有理数的识别
课堂小结
利用勾股定理发现非有理数
已知一个直角三角形的两条直角边长分别为1和 2,算一算斜边长x的平方 ,x是整数(或分数)吗?
x2=?
1
2
x
导入新知
1.通过拼图活动和勾股定理的应用感受无理数产生的实际背景和引入的必要性.
2.能判断一个数是否为有理数.
素养目标
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形
剪一剪 拼一拼
1
1
1
1
探究一: 下面请同学们拿出准备好的两个边长为1的小正方形
探究新知
知识点 1
利用拼图发现非有理数
1
1
方法一
探究新知
思考:设大正方形的边长为a,则a满足什么条件?
方
法
二
探究新知
a2=2
2.a可能是分数吗?说说你的理由.
探究二:
1.a可能是整数吗?说说你的理由.
探究新知
a2=2
a
因为a2=2,1
因为
所以a一定不是分数.
在等式a2=2中,a既不是整数,也不是分数,那么一定不是有理数.
探究新知
即两个相同最简分数的乘积仍是分数.
a2=2
a
归纳总结
有理数包括:整数和分数.
如果一个数既不是整数也不是分数,
那么这个数不是有理数.
在a2=2中,a不是有理数.
探究新知
例 如图,有一个由五个边长为1的小正方形组成的图形,我们可以把它剪拼成一个正方形.则拼成的正方形的面积是多少?这个正方形的边长是有理数吗?
解:因为小正方形的边长为1,
所以每个小正方形的面积为1,
所以拼成的正方形的面积为 5×1=5.
因为找不到平方等于5的有理数,
所以这个正方形的边长不是有理数.
探究新知
素养考点 1
非有理数的识别
提示:解决本题的关键是理解五个小正方形的面积的和就是拼成的正方形的面积.
1.满足下列条件的数a不是有理数的是 ( )
A.2a+5=8 B.a2=0.16
C.a2=7 D.a2=9
2.下列说法:①有理数都是有限小数;②有限小数都是有理数;③有理数都是无限循环小数;④无限循环小数都是有理数.其中正确的有 ( )
A.①② B.①③ C.②③ D.②④
C
D
巩固练习
变式训练
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,则b应满足什么条件?b是有理数吗?
解:b2=5.①因为22=4,32=9,4<5<9,
所以b不可能是整数.
②没有两个相同的分数相乘得5,故b不可能是分数.
③因为没有一个整数或分数的平方为5,所以b不是有理数.
探究新知
知识点 2
利用勾股定理发现非有理数
解:两条直角边分别为1和2,根据勾股定理,得12+22=5,所以正方形的面积是5.
像上面讨论的数a,b都不是有理数,而是另一类数—无理数.
早在公元前,古希腊数学家毕达哥拉斯认为万物皆“数”,即“宇宙间的一切现象都能归结为整数或整数之比”.但是这个学派中的一个叫希伯索斯的成员却发现边长为1的正方形的对角线的长不能用整数或整数之比来表示,这个发现动摇了毕达哥拉斯学派的信条,据说为此希伯索斯被投进了大海,他为真理而献出了宝贵的生命,但真理是不可战胜的,后来古希腊人终于正视了希伯索斯的发现.也就是a2=2中的a不是有理数.
探究新知
用生命换来的新数
归纳总结
例 如图,在△ABC中,CD⊥AB,垂足为D,AC=6,AD=5,问:CD可能是整数吗?可能是分数吗?可能是有理数吗?
解:在Rt△ACD中,AC为斜边,AC=6,AD=5,所以CD2=AC2-AD2=11.因为11是质数,大于1的整数的平方都是合数,所以11不能写成一个整数的平方,所以CD不可能是整数.
因为最简分数的平方仍是分数,所以CD不可能是分数.所以CD不可能是有理数.
素养考点 1
利用勾股定理识别非有理数
探究新知
如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
解:由正三角形的性质可知BD=1,在Rt△ABD中,
由勾股定理得h2=3.h不可能是整数,也不可能是分数.
巩固练习
变式训练
连接中考
D
(2020·威海模拟)下列正方形的边长不是有理数的是( )
A. 面积为2.56的正方形 B.面积为36的正方形
C.面积为 的正方形 D.面积为10的正方形
1 .满足下列条件的数不是有理数的是( )
课堂检测
基础巩固题
C
2.两直角边分别是3和5的直角三角形的斜边长是( )
A. 整数 B. 分数
C. 有理数 D.非有理数
D
C.a2=3
D.2a2=18
B. a2=0.36
A. 2a +5=8
D
2
不是
3.如果方程x2=m 的解是有理数,则数m不能取下列四个数中的( )
A. 1 B. 4 C. 0.25 D.0.5
4.把边长是1的两个正方形纸片重新剪裁成一个大的正方形,则大正方形的面积是______,它的边长_____有理数(填写“是”或“不是”)
课堂检测
基础巩固题
请你在方格纸上按照如下要求设计直角三角形.(所作三角形的各个顶点均在格点上)
(1)使它的一边为有理数,另两边边长不是有理数;
(2)使它的三边边长都是有理数.
能力提升题
课堂检测
解:(1)如图1所示.
(2)如图2所示.
图1
图2
能力提升题
课堂检测
在下列4×4的网格中,每个小正方形的边长都为1,请在每一个图中分别画出一条线段,且它们的长度均表示不等的非有理数.
拓广探索题
课堂检测
解:答案不唯一.如图所示:
AB2=2,2不能写成一个整数或分数的平方,所以AB表示的数是非有理数.
CD2=8,8不能写成一个整数或分数的平方,所以CD表示的数是非有理数.
EF2=18,18不能写成一个整数或分数的平方,所以EF表示的数是非有理数.
拓广探索题
课堂检测
非有理数的发现
拼图发现
首先通过拼图把几个小正方形拼成一个大正方形,然后利用面积发现非有理数
非有理数的识别
课堂小结
利用勾股定理发现非有理数
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
