北师大版数学八年级上册2.1 认识无理数课件(第2课时 23张)
文档属性
| 名称 | 北师大版数学八年级上册2.1 认识无理数课件(第2课时 23张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 907.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览







文档简介
2.1 认识无理数(第2课时)
思考导入
1.有理数如何分类?
有理数
整数(如-1,0,2,3,… ):都可看成有限小数
分数(如 … ):如何化成小数?可不可能都化成有限小数或无限循环小数?
2.上节课了解到一些数,如a2=2,b2=5中的a,b 既不是整数,也不是分数,那么它们究竟是什么数呢?
导入新知
1.借助计算器探索无理数是无限不循环小数,并从中体会无限逼近的思想.
2.无理数概念的建立及估算,会判断一个数是有理数还是无理数.
素养目标
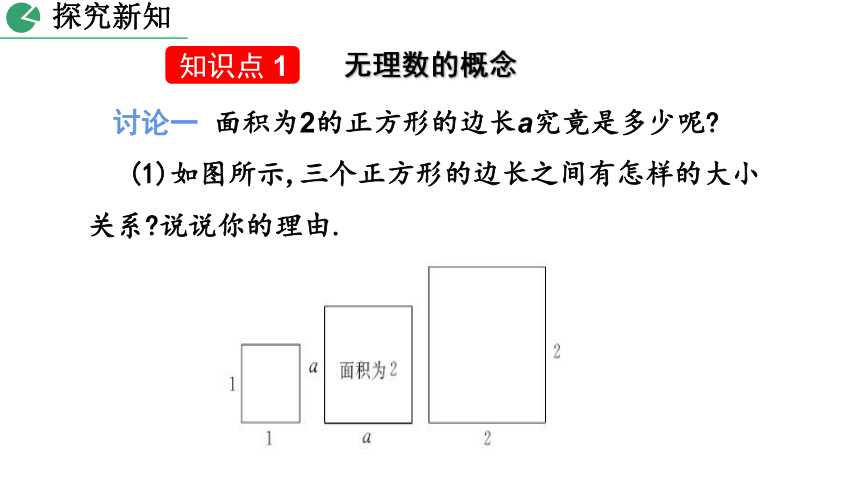
讨论一 面积为2的正方形的边长a究竟是多少呢?
(1)如图所示,三个正方形的边长之间有怎样的大小关系?说说你的理由.
知识点 1
无理数的概念
探究新知
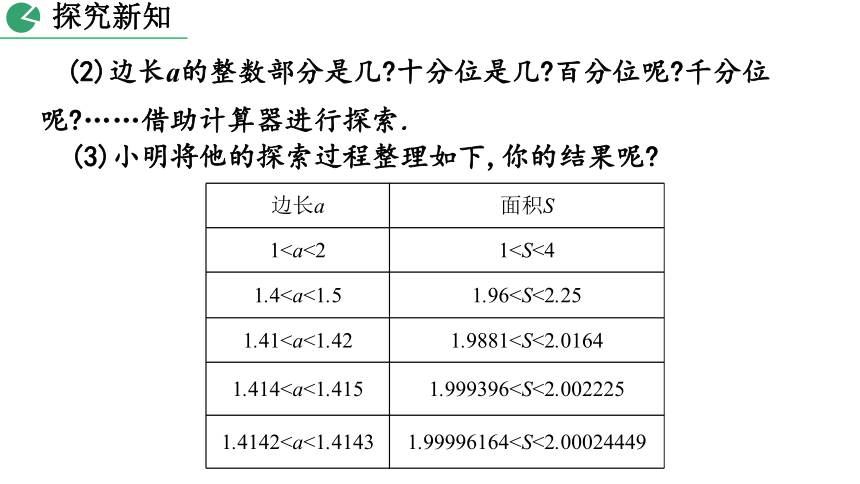
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索.
(3)小明将他的探索过程整理如下,你的结果呢?
边长a
面积S
111.41.961.411.98811.4141.9993961.41421.99996164探究新知
【归纳总结】a 是介于1和2之间的一个数,既不是整数,也不是分数,则 a 一定不是有理数.如果写成小数形式,它是有限小数吗?
事实上,a=1.41421356…,它是一个无限不循环小数.
探究新知
思考 a的范围在哪两个数之间?左面的边长中,前面的数值和后面的数值相比,哪个更接近正方形的实际边长?
用上面的方法估计面积为5的正方形的边长b的值.边长b会不会算到某一位时,它的平方恰好等于5?
如果b算到某一位时,它的平方恰好等于5,即b是一个有限小数,那么它的平方一定是一个有限小数,而不可能是5,所以b不可能是有限小数.事实上,b=2.236 067 978…它是一个无限不循环小数.
同样,对于体积为2的正方体,借用计算器,可以得到它的棱长c=1.259 921 05…,它也是一个无限不循环小数.
探究新知
想一想
讨论二 把下列各数表示成小数,你发现了什么?
3,
解:3=3.0
分数化成小数,最终此小数的形式有哪几种情况?
分数只能化成有限小数或无限循环小数,即任何有限小数或无限循环小数都是有理数.
探究新知
像0.585885888588885…,1.41421356…, -2.2360679…等这些数的小数位数都是无限的,并且不是循环的,它们都是无限不循环小数.
我们把无限不循环小数称为无理数.
(圆周率π=3.14159265…也是一个无限不循环小数,故π是无理数).
你能找到其他的无理数吗?
探究新知
???无理数的概念
提示 有理数与无理数的区别:①有理数是有限小数或无限循环小数,而无理数是无限不循环小数;②所有的有理数都能化成分数(整数可以看成是分母为1的分数),而无理数不能化成分数.注意:?形似分数,但它不是分数,是无理数.
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}概念
无限不循环小数
分类
正无理数和负无理数
三种常见类型
根号型:含有根号,开方开不尽,例如: (以后学习)
含有圆周率型:例如:π,0.7π
构造型:例如:0.3030030003…(相邻两个3之间依次多一个3)
下列各数中,哪些是有理数?哪些是无理数?
3.14 , , 0.57
0.101 000 100 000 1……(相邻两个1之间0的个数逐次加2).
解:有理数有 ,
0.57
无理数有 0.101 000 100 000 1…
. .
. .
3.14
(因为3.14是有限小数)
. .
(因为0.57是无限循环小数)
(因为它是无限不循环小数)
探究新知
例
1.在 ? ,0,3.14,-0.?,6.751 755 175 551 7…(7和1之间5的个数逐次加1),-?中,无理数有 ????个.
2
1 认识无理数
巩固练习
2.下列各数是无理数的是 ( )
A.1 B.-0.6
C.-6 D.π
D
面积为3的正方形的边长为a.
(1)a的整数部分是几?
(2)估计a的值.(结果精确到百分位)
分析:利用“夹逼法”进行估计即可.
解:(1)因为a2=3,1<3<4,
所以1<a<2,
所以a的整数部分为1.
(2)当1.7<a<1.8时,
无理数的估计
探究新知
2.89<a2<3.24,
所以a的十分位是7.
当1.73<a<1.74时,
2.9929<a2<3.0276,
所以a的百分位是3.所以a≈1.73 .
知识点 2
1.若边长为a cm的正方形的面积与长、宽分别为8 cm、4 cm的长方形的面积相等,则a的取值在 ( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
D
巩固练习
2.一块面积为10的正方形草坪,其边长( )
A.小于3 B. 等于3
C.在3与4之间 D.大于4
C
连接中考
C
1.(2019?邵阳)下列各数中,属于无理数的是( )
A. B.1.414 C. D.
B
2.(2019?白银)下列整数中,与 最接近的整数是( )
A.3 B.4 C.5 D.6
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( )
1. 判断题
╳
√
√
╳
课堂检测
基础巩固题
2.以下各正方形的边长是无理数的是( )
A.面积为25的正方形;
B.面积为 的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
C
课堂检测
基础巩固题
3 .下列各数,是大于-3而小于-4的无理数的是( )
A.-2.56879 B.-3.121221222…
C.- D.2.383883888…
4.请你写出一个大于2且小于4的无理数: .
基础巩固题
课堂检测
B
π
5.如图是面积分别为1,2,3,4,5,6,7,8,9的正方形.边长是有理数的正方形有_____个,边长是无理数的正方形有_____个.
3
6
基础巩固题
课堂检测
如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度为有理数的线段是 ????.
?
1 认识无理数
课堂检测
能力提升题
CD,EF
解析:设小正方形的边长为x,则x2=2.
因为AB2=x2+(3x)2=10x2=20,所以AB的长不是有理数.
因为CD2=(2x)2+(2x)2=8x2=16,CD=4,即CD的长是有理数.
因为EF2=x2+x2=2x2=4,EF=2,即EF的长是有理数.
因为GH2=x2+(2x)2=5x2=10,所以GH的长不是有理数.
小明买了一盒饮料,盒子的尺寸为5×4×3(单位:cm),
现在小明要将这盒饮料分别倒在两个同样大小的正方体容器内,问这两个正方体容器的棱长是有理数还是无理数?请说说你的理由.若是无理数,请你利用计算器探索这个正方体的棱长至少为多少?(精确到十分位)
解:设此正方体的棱长为x cm,则2x3=5×4×3,x3=30.
因为33=27,43=64,3即x不是有理数,而是无理数.因为3.13<30<3.23,
所以3.1课堂检测
拓广探索题
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
思考导入
1.有理数如何分类?
有理数
整数(如-1,0,2,3,… ):都可看成有限小数
分数(如 … ):如何化成小数?可不可能都化成有限小数或无限循环小数?
2.上节课了解到一些数,如a2=2,b2=5中的a,b 既不是整数,也不是分数,那么它们究竟是什么数呢?
导入新知
1.借助计算器探索无理数是无限不循环小数,并从中体会无限逼近的思想.
2.无理数概念的建立及估算,会判断一个数是有理数还是无理数.
素养目标
讨论一 面积为2的正方形的边长a究竟是多少呢?
(1)如图所示,三个正方形的边长之间有怎样的大小关系?说说你的理由.
知识点 1
无理数的概念
探究新知
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索.
(3)小明将他的探索过程整理如下,你的结果呢?
边长a
面积S
1
【归纳总结】a 是介于1和2之间的一个数,既不是整数,也不是分数,则 a 一定不是有理数.如果写成小数形式,它是有限小数吗?
事实上,a=1.41421356…,它是一个无限不循环小数.
探究新知
思考 a的范围在哪两个数之间?左面的边长中,前面的数值和后面的数值相比,哪个更接近正方形的实际边长?
用上面的方法估计面积为5的正方形的边长b的值.边长b会不会算到某一位时,它的平方恰好等于5?
如果b算到某一位时,它的平方恰好等于5,即b是一个有限小数,那么它的平方一定是一个有限小数,而不可能是5,所以b不可能是有限小数.事实上,b=2.236 067 978…它是一个无限不循环小数.
同样,对于体积为2的正方体,借用计算器,可以得到它的棱长c=1.259 921 05…,它也是一个无限不循环小数.
探究新知
想一想
讨论二 把下列各数表示成小数,你发现了什么?
3,
解:3=3.0
分数化成小数,最终此小数的形式有哪几种情况?
分数只能化成有限小数或无限循环小数,即任何有限小数或无限循环小数都是有理数.
探究新知
像0.585885888588885…,1.41421356…, -2.2360679…等这些数的小数位数都是无限的,并且不是循环的,它们都是无限不循环小数.
我们把无限不循环小数称为无理数.
(圆周率π=3.14159265…也是一个无限不循环小数,故π是无理数).
你能找到其他的无理数吗?
探究新知
???无理数的概念
提示 有理数与无理数的区别:①有理数是有限小数或无限循环小数,而无理数是无限不循环小数;②所有的有理数都能化成分数(整数可以看成是分母为1的分数),而无理数不能化成分数.注意:?形似分数,但它不是分数,是无理数.
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}概念
无限不循环小数
分类
正无理数和负无理数
三种常见类型
根号型:含有根号,开方开不尽,例如: (以后学习)
含有圆周率型:例如:π,0.7π
构造型:例如:0.3030030003…(相邻两个3之间依次多一个3)
下列各数中,哪些是有理数?哪些是无理数?
3.14 , , 0.57
0.101 000 100 000 1……(相邻两个1之间0的个数逐次加2).
解:有理数有 ,
0.57
无理数有 0.101 000 100 000 1…
. .
. .
3.14
(因为3.14是有限小数)
. .
(因为0.57是无限循环小数)
(因为它是无限不循环小数)
探究新知
例
1.在 ? ,0,3.14,-0.?,6.751 755 175 551 7…(7和1之间5的个数逐次加1),-?中,无理数有 ????个.
2
1 认识无理数
巩固练习
2.下列各数是无理数的是 ( )
A.1 B.-0.6
C.-6 D.π
D
面积为3的正方形的边长为a.
(1)a的整数部分是几?
(2)估计a的值.(结果精确到百分位)
分析:利用“夹逼法”进行估计即可.
解:(1)因为a2=3,1<3<4,
所以1<a<2,
所以a的整数部分为1.
(2)当1.7<a<1.8时,
无理数的估计
探究新知
2.89<a2<3.24,
所以a的十分位是7.
当1.73<a<1.74时,
2.9929<a2<3.0276,
所以a的百分位是3.所以a≈1.73 .
知识点 2
1.若边长为a cm的正方形的面积与长、宽分别为8 cm、4 cm的长方形的面积相等,则a的取值在 ( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
D
巩固练习
2.一块面积为10的正方形草坪,其边长( )
A.小于3 B. 等于3
C.在3与4之间 D.大于4
C
连接中考
C
1.(2019?邵阳)下列各数中,属于无理数的是( )
A. B.1.414 C. D.
B
2.(2019?白银)下列整数中,与 最接近的整数是( )
A.3 B.4 C.5 D.6
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( )
1. 判断题
╳
√
√
╳
课堂检测
基础巩固题
2.以下各正方形的边长是无理数的是( )
A.面积为25的正方形;
B.面积为 的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
C
课堂检测
基础巩固题
3 .下列各数,是大于-3而小于-4的无理数的是( )
A.-2.56879 B.-3.121221222…
C.- D.2.383883888…
4.请你写出一个大于2且小于4的无理数: .
基础巩固题
课堂检测
B
π
5.如图是面积分别为1,2,3,4,5,6,7,8,9的正方形.边长是有理数的正方形有_____个,边长是无理数的正方形有_____个.
3
6
基础巩固题
课堂检测
如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度为有理数的线段是 ????.
?
1 认识无理数
课堂检测
能力提升题
CD,EF
解析:设小正方形的边长为x,则x2=2.
因为AB2=x2+(3x)2=10x2=20,所以AB的长不是有理数.
因为CD2=(2x)2+(2x)2=8x2=16,CD=4,即CD的长是有理数.
因为EF2=x2+x2=2x2=4,EF=2,即EF的长是有理数.
因为GH2=x2+(2x)2=5x2=10,所以GH的长不是有理数.
小明买了一盒饮料,盒子的尺寸为5×4×3(单位:cm),
现在小明要将这盒饮料分别倒在两个同样大小的正方体容器内,问这两个正方体容器的棱长是有理数还是无理数?请说说你的理由.若是无理数,请你利用计算器探索这个正方体的棱长至少为多少?(精确到十分位)
解:设此正方体的棱长为x cm,则2x3=5×4×3,x3=30.
因为33=27,43=64,3
所以3.1
拓广探索题
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
