北师大版数学七年级上册2.12 用计算器进行运算 课件(20张)
文档属性
| 名称 | 北师大版数学七年级上册2.12 用计算器进行运算 课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 14:50:32 | ||
图片预览








文档简介
2.12 用计算器进行运算
导入新知
观察右图中展示的计算器,试着摸索各个按键的功能.
素养目标
1.会使用计算器进行有理数的加、减、乘、除、乘方运算及其混合运算.
2.能运用计算器解决实际问题中的复杂运算.
3.经历运用计算器探求规律的活动,发展合情推理能力.
探究新知
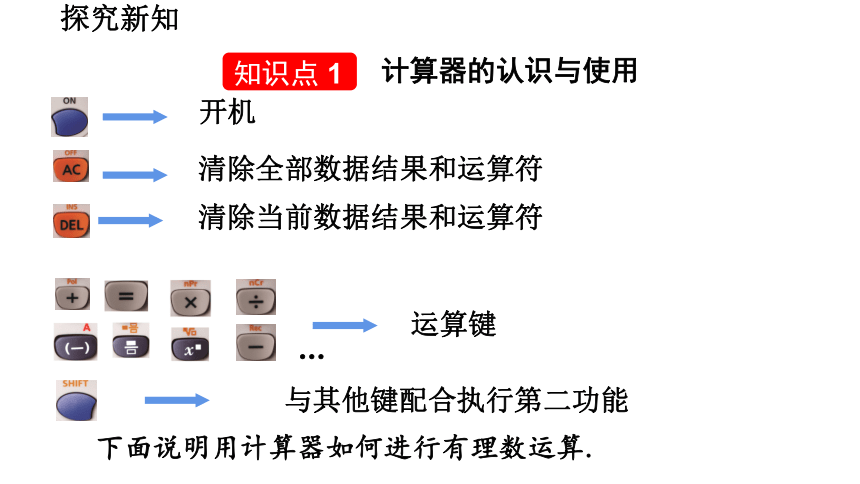
知识点 1
计算器的认识与使用
开机
清除全部数据结果和运算符
清除当前数据结果和运算符
运算键
与其他键配合执行第二功能
…
下面说明用计算器如何进行有理数运算.
探究新知
素养考点
利用计算器进行有理数的混合运算
例 用计算器计算:
-8×3+4÷(-2).
解:按键顺序为
(—)
8
×
3
+
4
÷
(—)
2
-26.
方法点拨:利用计算器计算时,一定要按照算式的书写顺序输入,即按从左到右的顺序输入.
显示结果为
=
巩固练习
变式训练
用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示结果:
-32768.
=
)
(-)
(
<
3
6
显示结果:
所以(-8)5=-32768,(-3)6=729.
729
探究新知
知识点 2
近似数与精确度
观察下列语句中的数据,试着发现它们的不同之处.
参加今天会议的有513人.
约有五百人参加了今天的会议.
确切反映实际人数.
只是接近实际人数.
定义:能够确切反映实际情况的数据叫做准确数,
表示与实际数据有差异的数据叫做近似数.
探究新知
宇宙现在的年龄约为200亿岁
长江长约6300km
圆周率约为3.14
近似数
近似数
近似数
素养考点
近似数和精确度的计算
例 按括号内的要求,用四舍五入法对下列各数取近似数:
探究新知
(1)0.0158(精确到0.001);(2)304.35(精确到个位);
(3)1.804(精确到0.1); (4)1.804(精确到0.01).
(4)1.804≈1.80.
解:(1)0.0158 ≈0.016;
(2)304.35≈304;
(3)1.804 ≈1.8;
方法点拨:判定精确程度的方法:在说明一个数的精确度时,主要看最后一个有效数字所在的数位,在哪一位就说成精确到哪一位.
巩固练习
变式训练
按要求对3.14159分别取近似数,下面结果错误的是( )
A.3.1(精确到0.1)
B.3.14(精确到0.01)
C.3.141(精确到0.001)
D.3.1416(精确到0.0001)
C
连接中考
(2019·山东省中考真题)与下面科学计算器的按键顺序:
对应的计算任务是( )
A.
B.
C.
D.
B
课堂检测
基础巩固题
1.用计算器计算:(1)(-7)3; (2)134.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
7
3
显示结果为:
-343.
=
)
(-)
(
<
1
4
显示显示结果为:
28561.
3
课堂检测
基础巩固题
2.下面数据中,是准确数的是( )
A.珠穆朗玛峰高出海平面约8844米
B.人的大脑有10000000000个细胞
C.小明买了5本小说
D.有关部门预测,到2020年轿车的拥有率将达到30%
C
课堂检测
基础巩固题
3.由四舍五入法得到的近似数是3.75,下面的数中不可能是原数的是( )
A.3.7514 B.3.7493 C.3.7504 D.3.755
D
4.下列说法中,正确的是( )
A.近似数2.4万精确到万位 B.近似数24000精确到千位
C.近似数2.4×104精确到千位 D.近似数2.4万精确到0.1
C
课堂检测
基础巩固题
5.近似数2.70所表示的准确数a的范围是( )
A.2.695≤a<2.705 B.2.65≤a<2.75
C.2.695<a≤2.705 D.2.65<a≤2.75
A
能力提升题
课堂检测
用四舍五入法对下列各数按要求取近似数:
(1)8.026(精确到0.01);
(2)549.49(精确到个位);
(3)999653(精确到千位);
(4)3.09×104(精确到千位).
(4)3.09×104≈3.1×104.
解:(1)8.026≈8.03;
(2)549.49≈549;
(3)999653≈1.000×105;
拓广探索题
课堂检测
使用计算器计算下列各式:
1×9+2=
12×9+3=
123×9+4=
1 234×9+5=
…
123 456 789×9+10=
通过计算,你发现了什么规律?
拓广探索题
课堂检测
解:1×9+2=11,
12×9+3=111,
123×9+4=1 111,
1 234×9+5=11 111,
…
123 456 789×9+10=1 111 111 111,
发现1×9+2的结果是两个1组成的数,12×9+3是由三个1组成的三位数……123 456 789×9+10的结果是由10个1组成的十位数.
用计算器进行运算
计算器的认识与使用
近似数
课堂小结
表示与实际数据有差异的数据叫做近似数
能够确切反映实际情况的数据叫做准确数
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
导入新知
观察右图中展示的计算器,试着摸索各个按键的功能.
素养目标
1.会使用计算器进行有理数的加、减、乘、除、乘方运算及其混合运算.
2.能运用计算器解决实际问题中的复杂运算.
3.经历运用计算器探求规律的活动,发展合情推理能力.
探究新知
知识点 1
计算器的认识与使用
开机
清除全部数据结果和运算符
清除当前数据结果和运算符
运算键
与其他键配合执行第二功能
…
下面说明用计算器如何进行有理数运算.
探究新知
素养考点
利用计算器进行有理数的混合运算
例 用计算器计算:
-8×3+4÷(-2).
解:按键顺序为
(—)
8
×
3
+
4
÷
(—)
2
-26.
方法点拨:利用计算器计算时,一定要按照算式的书写顺序输入,即按从左到右的顺序输入.
显示结果为
=
巩固练习
变式训练
用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示结果:
-32768.
=
)
(-)
(
<
3
6
显示结果:
所以(-8)5=-32768,(-3)6=729.
729
探究新知
知识点 2
近似数与精确度
观察下列语句中的数据,试着发现它们的不同之处.
参加今天会议的有513人.
约有五百人参加了今天的会议.
确切反映实际人数.
只是接近实际人数.
定义:能够确切反映实际情况的数据叫做准确数,
表示与实际数据有差异的数据叫做近似数.
探究新知
宇宙现在的年龄约为200亿岁
长江长约6300km
圆周率约为3.14
近似数
近似数
近似数
素养考点
近似数和精确度的计算
例 按括号内的要求,用四舍五入法对下列各数取近似数:
探究新知
(1)0.0158(精确到0.001);(2)304.35(精确到个位);
(3)1.804(精确到0.1); (4)1.804(精确到0.01).
(4)1.804≈1.80.
解:(1)0.0158 ≈0.016;
(2)304.35≈304;
(3)1.804 ≈1.8;
方法点拨:判定精确程度的方法:在说明一个数的精确度时,主要看最后一个有效数字所在的数位,在哪一位就说成精确到哪一位.
巩固练习
变式训练
按要求对3.14159分别取近似数,下面结果错误的是( )
A.3.1(精确到0.1)
B.3.14(精确到0.01)
C.3.141(精确到0.001)
D.3.1416(精确到0.0001)
C
连接中考
(2019·山东省中考真题)与下面科学计算器的按键顺序:
对应的计算任务是( )
A.
B.
C.
D.
B
课堂检测
基础巩固题
1.用计算器计算:(1)(-7)3; (2)134.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
7
3
显示结果为:
-343.
=
)
(-)
(
<
1
4
显示显示结果为:
28561.
3
课堂检测
基础巩固题
2.下面数据中,是准确数的是( )
A.珠穆朗玛峰高出海平面约8844米
B.人的大脑有10000000000个细胞
C.小明买了5本小说
D.有关部门预测,到2020年轿车的拥有率将达到30%
C
课堂检测
基础巩固题
3.由四舍五入法得到的近似数是3.75,下面的数中不可能是原数的是( )
A.3.7514 B.3.7493 C.3.7504 D.3.755
D
4.下列说法中,正确的是( )
A.近似数2.4万精确到万位 B.近似数24000精确到千位
C.近似数2.4×104精确到千位 D.近似数2.4万精确到0.1
C
课堂检测
基础巩固题
5.近似数2.70所表示的准确数a的范围是( )
A.2.695≤a<2.705 B.2.65≤a<2.75
C.2.695<a≤2.705 D.2.65<a≤2.75
A
能力提升题
课堂检测
用四舍五入法对下列各数按要求取近似数:
(1)8.026(精确到0.01);
(2)549.49(精确到个位);
(3)999653(精确到千位);
(4)3.09×104(精确到千位).
(4)3.09×104≈3.1×104.
解:(1)8.026≈8.03;
(2)549.49≈549;
(3)999653≈1.000×105;
拓广探索题
课堂检测
使用计算器计算下列各式:
1×9+2=
12×9+3=
123×9+4=
1 234×9+5=
…
123 456 789×9+10=
通过计算,你发现了什么规律?
拓广探索题
课堂检测
解:1×9+2=11,
12×9+3=111,
123×9+4=1 111,
1 234×9+5=11 111,
…
123 456 789×9+10=1 111 111 111,
发现1×9+2的结果是两个1组成的数,12×9+3是由三个1组成的三位数……123 456 789×9+10的结果是由10个1组成的十位数.
用计算器进行运算
计算器的认识与使用
近似数
课堂小结
表示与实际数据有差异的数据叫做近似数
能够确切反映实际情况的数据叫做准确数
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
