人教版数学九年级上册23.1 图形的旋转同步练习(解析版)
文档属性
| 名称 | 人教版数学九年级上册23.1 图形的旋转同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 305.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 00:00:00 | ||
图片预览


文档简介
23.1图形的旋转同步练习(三)
一、选择题
1、下列运动属于旋转的是(
)
A.
滚动过程中的篮球的滚动
B.
钟表的钟摆的摆动
C.
气球升空的运动
D.
一个图形沿某直线对折的过程
2、下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是(
)
A.
B.
C.
D.
3、下列汽车标志中,是旋转对称图形但不是轴对称图形的有(
)
A.
2个
B.
3个
C.
4个
D.
5个
4、下列每组大写字母中,旋转180°和原来形状一样的是(
)
A.
HIOE
B.
HION
C.
HIOU
D.
HIOB
5、如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2019秒时,菱形两对角线交点D的横坐标为(
)
A.
B.
-
C.
1
D.
-1
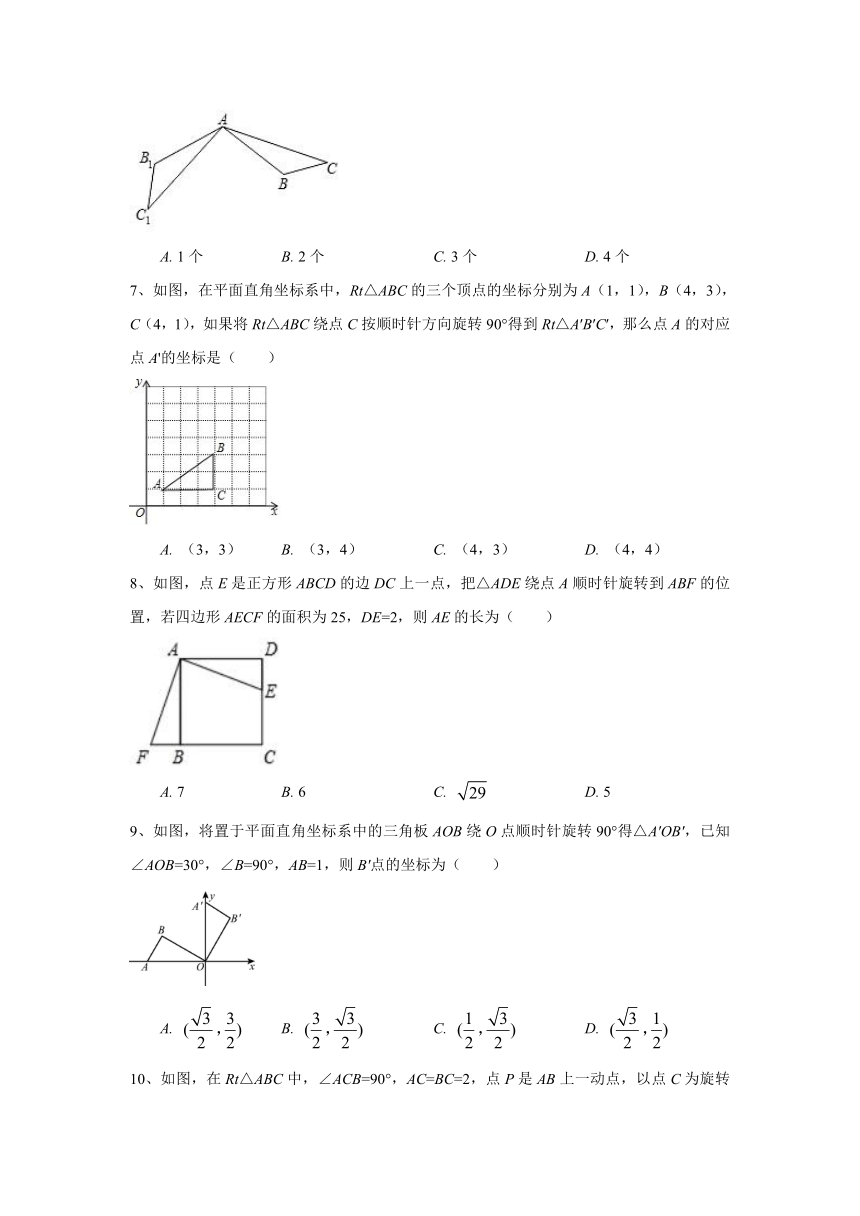
6、如图,将△ABC绕点A旋转到△AB1C1,下列说法正确的个数有(
)
(1)AC=AB;(2)BC=B1C1;(3)∠BAC=∠B1AC1;(4)∠CAC1=∠BAB1.
A.
1个
B.
2个
C.
3个
D.
4个
7、如图,在平面直角坐标系中,Rt△ABC的三个顶点的坐标分别为A(1,1),B(4,3),C(4,1),如果将Rt△ABC绕点C按顺时针方向旋转90°得到Rt△A′B′C′,那么点A的对应点A'的坐标是(
)
A.
(3,3)
B.
(3,4)
C.
(4,3)
D.
(4,4)
8、如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转到ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为(
)
A.
7
B.
6
C.
D.
5
9、如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB',已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为(
)
A.
B.
C.
D.
10、如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,点P是AB上一动点,以点C为旋转中心,将△ACP顺时针旋转到△BCQ的位置,则PQ最小值为(
)
A.
B.
2
C.
D.
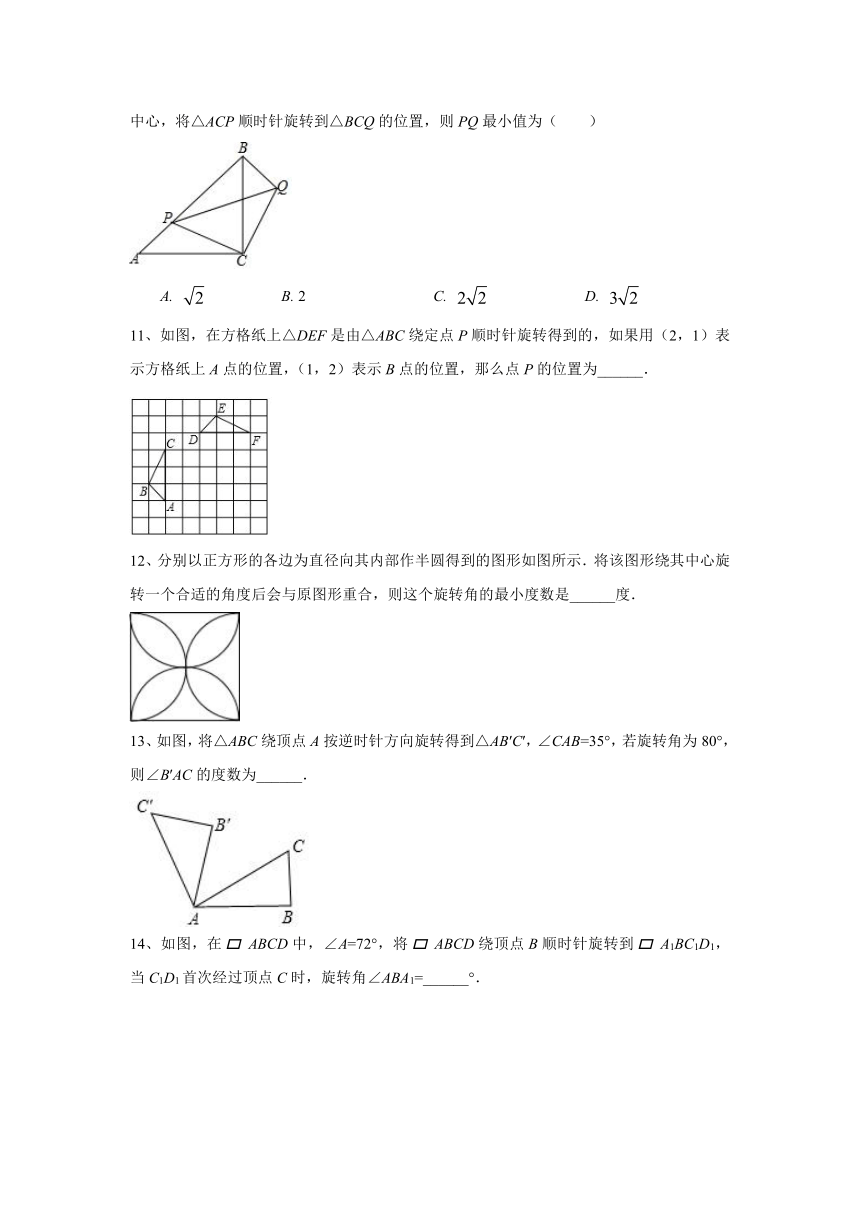
11、如图,在方格纸上△DEF是由△ABC绕定点P顺时针旋转得到的,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,那么点P的位置为______.
12、分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是______度.
13、如图,将△ABC绕顶点A按逆时针方向旋转得到△AB′C′,∠CAB=35°,若旋转角为80°,则∠B′AC的度数为______.
14、如图,在ABCD中,∠A=72°,将ABCD绕顶点B顺时针旋转到A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=______°.
15、如图,等边三角形ABC内有一点P,分別连接AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC=______.
16、如图,在平面直角坐标系中,方格纸中有一条美丽可爱的小金鱼,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1),在同一方格纸中,画出将小金鱼图案绕原点O旋转180°后得到的四边形A′B′C′D′,并求出A′,B′,C′,D′的坐标.
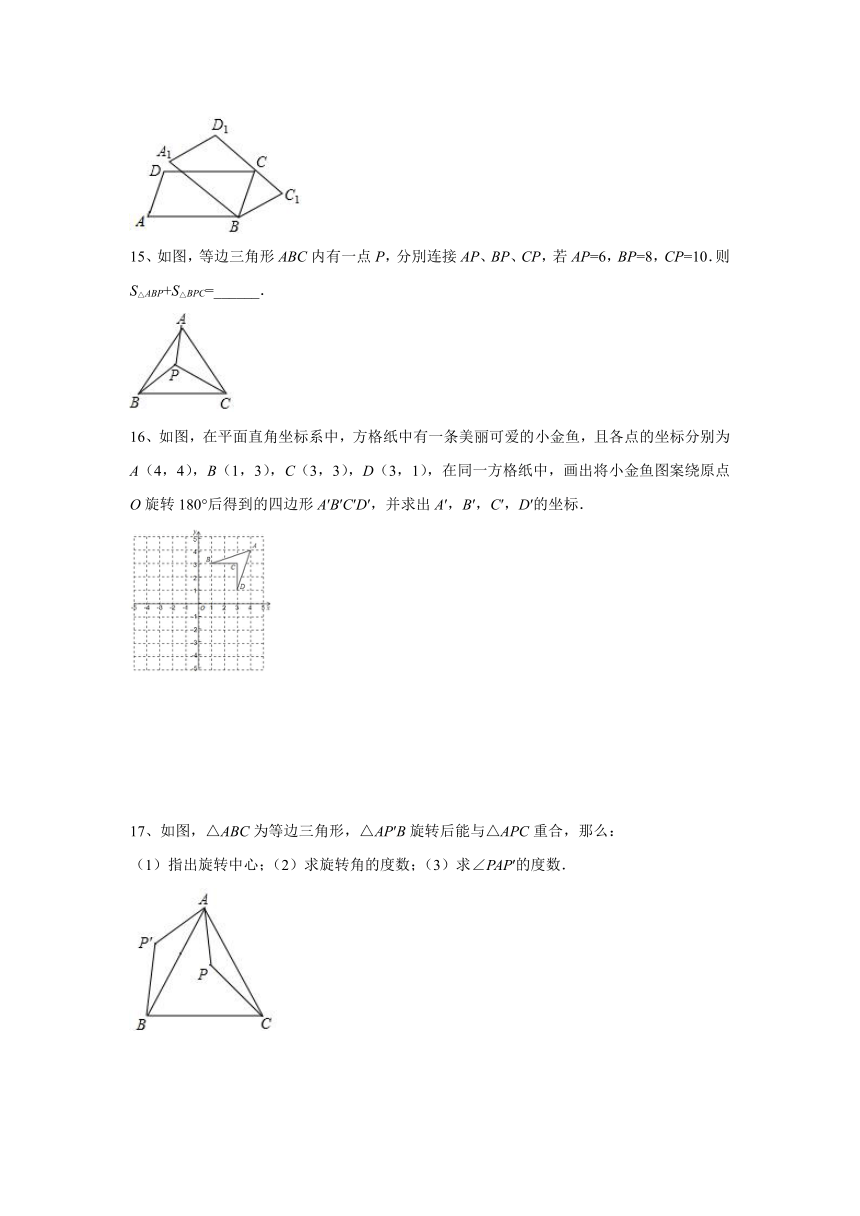
17、如图,△ABC为等边三角形,△AP′B旋转后能与△APC重合,那么:
(1)指出旋转中心;(2)求旋转角的度数;(3)求∠PAP′的度数.
18、如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,将△PAB绕A逆时针旋转90°得△DAC.
(1)试判断△PAD的形状并说明理由;
(2)连接PC,若∠APB=135°,PA=1,PB=3,求PC的长.
19、如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=,求AB的长.
20、如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
21、已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.
(1)问题发现
如图1,△CDE的形状是三角形.
(2)探究证明
如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
(3)解决问题
是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.
1、答案:B
分析:本题考查了旋转的概念.
解答:A、滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;
B、钟表的钟摆的摆动,符合旋转变换的定义,属于旋转;
C、气球升空的运动是平移,不属于旋转;
D、一个图形沿某直线对折的过程是轴对称,不属于旋转.选B.
2、答案:D
分析:本题考查了利用旋转设计图案.
解答:A.可由一个基本花瓣绕其中心经过7次旋转,每次旋转45度得到;
B.
可由一个基本菱形绕其中心经过5次旋转,每次旋转60度得到;
C.
可由一个基本花瓣绕其中心旋转180度得到;
D.
不能由基本图案旋转得到,选D.
3、答案:A
分析:本题考查了旋转对称图形.
解答:第1个图形,既是旋转对称图形,也是轴对称图形,
第2个图形,是旋转对称图形,不是轴对称图形,
第3个图形,不是旋转对称图形,是轴对称图形,
第4个图形,既是旋转对称图形,也是轴对称图形,
第5个图形,是旋转对称图形,不是轴对称图形.
∴是旋转对称图形但不是轴对称图形的有:第2个,第5个,共2个.选A.
4、答案:B
分析:本题考查了旋转的性质.
解答:根据旋转的性质,根据题意要求旋转180°和原来形状一样,
故旋转180°和原来形状一样的字母必须是中心对称的图形,
分析可得只有B的4个字母是中心对称的图形.选B.
5、答案:B
分析:本题考查了旋转的性质、菱形的性质.
解答:菱形OABC的顶点O(0,0),B(2,2),得D点坐标为(1,1).
∴OD=,每秒旋转45°,则第2019秒时,得45°×2019,45°×2019÷360=252.375周,
OD旋转了252周,菱形的对角线交点D的坐标为(-,0),选B.
6、答案:C
分析:本题考查了旋转的性质.
解答:根据旋转的性质,可知:(1)AC=AC1,故错误;(2)BC=B1C1,故正确;(3)∠BAC=∠B1AC1,故正确;(4)在(3)的基础上,结合等式的性质,得∠CAC1=∠BAB1.选C.
7、答案:D
分析:本题考查了旋转的性质.
解答:旋转后的Rt△A′B′C′如图所示,观察图象可知A′(4,4).
选D.
8、答案:C
分析:本题考查了旋转的性质、正方形的性质、勾股定理.
解答:∵把△ADE顺时针旋转△ABF的位置,
∴四边形AECF的面积等于正方形ABCD的面积等于25,∴AD=DC=5,
∵DE=2,∴Rt△ADE中,AE=,选
C.
9、答案:A
分析:本题考查了旋转的性质、勾股定理.
解答:如图,过点B作BC⊥OA于C,过点B'作B'C'⊥OA'于C',
在Rt△AOB中,∠AOB=30°,AB=1,∴OA=2,
根据勾股定理得,OB==,
在Rt△BOC中,BC=OB=,根据勾股定理得,OC==,
由旋转知,B'C'=BC=,OC'=OC=,,∴B′点的坐标为(,).选A.
10、答案:B
分析:本题考查了旋转的性质、等腰直角三角形的性质.
解答:∵将△ACP顺时针旋转到△BCQ的位置,
∴PC=CQ,∠PCQ=90°,
∴PQ2=PC2+CQ2=2PC2,
∴当PC最小时,PQ有最小值,即PC⊥AB时,PQ有最小值,
∵∠ACB=90°,AC=BC=2,
∴AB=2,且PC⊥AB,
∴PC=,
∴PQ的最小值为2,选B.
二、填空题
11、答案:(5,2)
分析:本题考查了旋转的概念、点的坐标.
解答:如图所示:作出对应点连线AD、BE、CF中任意两条中垂线的交点P,就是对称中心,∵(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,
∴点P的位置为:(5,2).故答案为:(5,2).
12、答案:90
分析:本题考查了旋转对称图形.
解答:图形可看作由一个基本图形每次旋转90°,旋转4次所组成,故最小旋转角为90°.
故答案为:90.
13、答案:45°
分析:本题考查了旋转的性质.
解答:∵△ABC绕顶点A按逆时针方向旋转80°得到△AB′C′,∴∠BAB′=80°,
∴∠B′AC=∠B′AB–∠CAB=80°–35°=45°.故答案为:45°.
14、答案:36
分析:本题考查了旋转的性质、平行四边形的性质.
解答:∵ABCD绕顶点B顺时针旋转到?A1BC1D1,
∴BC=BC1,
∴∠BCC1=∠C1,
∵∠A=72°,
∴∠BCC1=∠C1=72°,
∴∠BCC1=∠C1,
∴∠CBC1=180°–2×72°=36°,
∴∠ABA1=36°,故答案为:36.
15、答案:
分析:本题考查了旋转的性质、等边三角形的性质.
解答:如图,将△BPC绕点B逆时针旋转60°后得△AP'B,连接PP′,
根据旋转的性质可知,旋转角∠PBP′=∠CAB=60°,BP=BP′,
∴△BPP′为等边三角形,
∴BP′=BP=8=PP',
由旋转的性质可知,AP′=PC=10,
在△BPP′中,PP′=8,AP=6,由勾股定理的逆定理得,△APP′是直角三角形,
∴S△ABP+S△BPC=S四边形AP'BP=S△BP'B+S△AP'P=BP2+×PP'×AP=24+16,
故答案为:.
三、解答题
16、答案:见解答
分析:本题考查了旋转作图.
解答:
由图中可以看出A′(–4,–4),B′(–1,–3),C′(–3,–3),D′(–3,–1).
17、答案:见解答
分析:本题考查了旋转的概念和性质.
解答:(1)∵△AP′B旋转后能与△APC重合,
∴旋转中心是点A;
(2)旋转角是∠BAC=60°;
(3)由(2)得:∠P′AP=∠BAC=60°.
18、答案:见解答
分析:本题考查了旋转的性质、等腰直角三角形的判定、勾股定理.
解答:(1)△PAD为等腰直角三角形.理由如下:
∵将△PAB绕A逆时针旋转90°得△DAC,
∴∠DAP=90°,PA=DA,
∴△PAD为等腰直角三角形.
(2)由旋转知,
∴∠CDA=∠APB=135°,∠ADP=45°,CD=PB=3,
∴∠CDP=135°-∠ADP=90°,
∴CD⊥PD,
∴PD=AP+AD=2,
在Rt△PDC中,
∴CP=.
19、答案:见解答
分析:本题考查了旋转的性质、全等三角形的判定与性质.
解答:(1)∵将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,
∴△ABC≌△DBE,
∴∠BAC=∠CDF,
∵∠BAC+∠ACB=90°,
∴∠CDF+∠ACB=90°,
∴DF⊥AC,且点F是AC中点,
∴DF垂直平分AC,
∴AE=CE.
(2)∵△ABC≌△DBE,
∴BE=CE=,
∴CE=AE=2,
∴AB=AE+BE=2+.
20、答案:见解答
分析:本题考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质.
解答:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=A
D.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,∵,
∴△EAB≌△DAC,
∴∠AEB=∠ADC;
(2)如图,∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形,
∴∠AED=60°,
又∵∠AEB=∠ADC=105°,
∴∠BED=105°–60°=45°.
21、答案:见解答
分析:本题考查了旋转的性质、等边三角形的判定与性质、垂线段最短、直角三角形的判定.
解答:(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形,
故答案为:等边.
(2)存在,当6<t<10时,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE=AB+DE=4+DE,
由(1)知,△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,,
∴△BDE的最小周长.
(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,
∴当点D与点B重合时,不符合题意,
②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEB=60°,
∴∠CEB=30°,
∵∠CEB=∠CDA,
∴∠CDA=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA-DA=6-4=2,
∴m=2.
③当6<m<10时,由∠DBE=120°>90°,∴此时不存在.
④当m>10时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14,∴m=14,
综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.
一、选择题
1、下列运动属于旋转的是(
)
A.
滚动过程中的篮球的滚动
B.
钟表的钟摆的摆动
C.
气球升空的运动
D.
一个图形沿某直线对折的过程
2、下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是(
)
A.
B.
C.
D.
3、下列汽车标志中,是旋转对称图形但不是轴对称图形的有(
)
A.
2个
B.
3个
C.
4个
D.
5个
4、下列每组大写字母中,旋转180°和原来形状一样的是(
)
A.
HIOE
B.
HION
C.
HIOU
D.
HIOB
5、如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2019秒时,菱形两对角线交点D的横坐标为(
)
A.
B.
-
C.
1
D.
-1
6、如图,将△ABC绕点A旋转到△AB1C1,下列说法正确的个数有(
)
(1)AC=AB;(2)BC=B1C1;(3)∠BAC=∠B1AC1;(4)∠CAC1=∠BAB1.
A.
1个
B.
2个
C.
3个
D.
4个
7、如图,在平面直角坐标系中,Rt△ABC的三个顶点的坐标分别为A(1,1),B(4,3),C(4,1),如果将Rt△ABC绕点C按顺时针方向旋转90°得到Rt△A′B′C′,那么点A的对应点A'的坐标是(
)
A.
(3,3)
B.
(3,4)
C.
(4,3)
D.
(4,4)
8、如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转到ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为(
)
A.
7
B.
6
C.
D.
5
9、如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB',已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为(
)
A.
B.
C.
D.
10、如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,点P是AB上一动点,以点C为旋转中心,将△ACP顺时针旋转到△BCQ的位置,则PQ最小值为(
)
A.
B.
2
C.
D.
11、如图,在方格纸上△DEF是由△ABC绕定点P顺时针旋转得到的,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,那么点P的位置为______.
12、分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是______度.
13、如图,将△ABC绕顶点A按逆时针方向旋转得到△AB′C′,∠CAB=35°,若旋转角为80°,则∠B′AC的度数为______.
14、如图,在ABCD中,∠A=72°,将ABCD绕顶点B顺时针旋转到A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=______°.
15、如图,等边三角形ABC内有一点P,分別连接AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC=______.
16、如图,在平面直角坐标系中,方格纸中有一条美丽可爱的小金鱼,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1),在同一方格纸中,画出将小金鱼图案绕原点O旋转180°后得到的四边形A′B′C′D′,并求出A′,B′,C′,D′的坐标.
17、如图,△ABC为等边三角形,△AP′B旋转后能与△APC重合,那么:
(1)指出旋转中心;(2)求旋转角的度数;(3)求∠PAP′的度数.
18、如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,将△PAB绕A逆时针旋转90°得△DAC.
(1)试判断△PAD的形状并说明理由;
(2)连接PC,若∠APB=135°,PA=1,PB=3,求PC的长.
19、如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=,求AB的长.
20、如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
21、已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.
(1)问题发现
如图1,△CDE的形状是三角形.
(2)探究证明
如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
(3)解决问题
是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.
1、答案:B
分析:本题考查了旋转的概念.
解答:A、滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;
B、钟表的钟摆的摆动,符合旋转变换的定义,属于旋转;
C、气球升空的运动是平移,不属于旋转;
D、一个图形沿某直线对折的过程是轴对称,不属于旋转.选B.
2、答案:D
分析:本题考查了利用旋转设计图案.
解答:A.可由一个基本花瓣绕其中心经过7次旋转,每次旋转45度得到;
B.
可由一个基本菱形绕其中心经过5次旋转,每次旋转60度得到;
C.
可由一个基本花瓣绕其中心旋转180度得到;
D.
不能由基本图案旋转得到,选D.
3、答案:A
分析:本题考查了旋转对称图形.
解答:第1个图形,既是旋转对称图形,也是轴对称图形,
第2个图形,是旋转对称图形,不是轴对称图形,
第3个图形,不是旋转对称图形,是轴对称图形,
第4个图形,既是旋转对称图形,也是轴对称图形,
第5个图形,是旋转对称图形,不是轴对称图形.
∴是旋转对称图形但不是轴对称图形的有:第2个,第5个,共2个.选A.
4、答案:B
分析:本题考查了旋转的性质.
解答:根据旋转的性质,根据题意要求旋转180°和原来形状一样,
故旋转180°和原来形状一样的字母必须是中心对称的图形,
分析可得只有B的4个字母是中心对称的图形.选B.
5、答案:B
分析:本题考查了旋转的性质、菱形的性质.
解答:菱形OABC的顶点O(0,0),B(2,2),得D点坐标为(1,1).
∴OD=,每秒旋转45°,则第2019秒时,得45°×2019,45°×2019÷360=252.375周,
OD旋转了252周,菱形的对角线交点D的坐标为(-,0),选B.
6、答案:C
分析:本题考查了旋转的性质.
解答:根据旋转的性质,可知:(1)AC=AC1,故错误;(2)BC=B1C1,故正确;(3)∠BAC=∠B1AC1,故正确;(4)在(3)的基础上,结合等式的性质,得∠CAC1=∠BAB1.选C.
7、答案:D
分析:本题考查了旋转的性质.
解答:旋转后的Rt△A′B′C′如图所示,观察图象可知A′(4,4).
选D.
8、答案:C
分析:本题考查了旋转的性质、正方形的性质、勾股定理.
解答:∵把△ADE顺时针旋转△ABF的位置,
∴四边形AECF的面积等于正方形ABCD的面积等于25,∴AD=DC=5,
∵DE=2,∴Rt△ADE中,AE=,选
C.
9、答案:A
分析:本题考查了旋转的性质、勾股定理.
解答:如图,过点B作BC⊥OA于C,过点B'作B'C'⊥OA'于C',
在Rt△AOB中,∠AOB=30°,AB=1,∴OA=2,
根据勾股定理得,OB==,
在Rt△BOC中,BC=OB=,根据勾股定理得,OC==,
由旋转知,B'C'=BC=,OC'=OC=,,∴B′点的坐标为(,).选A.
10、答案:B
分析:本题考查了旋转的性质、等腰直角三角形的性质.
解答:∵将△ACP顺时针旋转到△BCQ的位置,
∴PC=CQ,∠PCQ=90°,
∴PQ2=PC2+CQ2=2PC2,
∴当PC最小时,PQ有最小值,即PC⊥AB时,PQ有最小值,
∵∠ACB=90°,AC=BC=2,
∴AB=2,且PC⊥AB,
∴PC=,
∴PQ的最小值为2,选B.
二、填空题
11、答案:(5,2)
分析:本题考查了旋转的概念、点的坐标.
解答:如图所示:作出对应点连线AD、BE、CF中任意两条中垂线的交点P,就是对称中心,∵(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,
∴点P的位置为:(5,2).故答案为:(5,2).
12、答案:90
分析:本题考查了旋转对称图形.
解答:图形可看作由一个基本图形每次旋转90°,旋转4次所组成,故最小旋转角为90°.
故答案为:90.
13、答案:45°
分析:本题考查了旋转的性质.
解答:∵△ABC绕顶点A按逆时针方向旋转80°得到△AB′C′,∴∠BAB′=80°,
∴∠B′AC=∠B′AB–∠CAB=80°–35°=45°.故答案为:45°.
14、答案:36
分析:本题考查了旋转的性质、平行四边形的性质.
解答:∵ABCD绕顶点B顺时针旋转到?A1BC1D1,
∴BC=BC1,
∴∠BCC1=∠C1,
∵∠A=72°,
∴∠BCC1=∠C1=72°,
∴∠BCC1=∠C1,
∴∠CBC1=180°–2×72°=36°,
∴∠ABA1=36°,故答案为:36.
15、答案:
分析:本题考查了旋转的性质、等边三角形的性质.
解答:如图,将△BPC绕点B逆时针旋转60°后得△AP'B,连接PP′,
根据旋转的性质可知,旋转角∠PBP′=∠CAB=60°,BP=BP′,
∴△BPP′为等边三角形,
∴BP′=BP=8=PP',
由旋转的性质可知,AP′=PC=10,
在△BPP′中,PP′=8,AP=6,由勾股定理的逆定理得,△APP′是直角三角形,
∴S△ABP+S△BPC=S四边形AP'BP=S△BP'B+S△AP'P=BP2+×PP'×AP=24+16,
故答案为:.
三、解答题
16、答案:见解答
分析:本题考查了旋转作图.
解答:
由图中可以看出A′(–4,–4),B′(–1,–3),C′(–3,–3),D′(–3,–1).
17、答案:见解答
分析:本题考查了旋转的概念和性质.
解答:(1)∵△AP′B旋转后能与△APC重合,
∴旋转中心是点A;
(2)旋转角是∠BAC=60°;
(3)由(2)得:∠P′AP=∠BAC=60°.
18、答案:见解答
分析:本题考查了旋转的性质、等腰直角三角形的判定、勾股定理.
解答:(1)△PAD为等腰直角三角形.理由如下:
∵将△PAB绕A逆时针旋转90°得△DAC,
∴∠DAP=90°,PA=DA,
∴△PAD为等腰直角三角形.
(2)由旋转知,
∴∠CDA=∠APB=135°,∠ADP=45°,CD=PB=3,
∴∠CDP=135°-∠ADP=90°,
∴CD⊥PD,
∴PD=AP+AD=2,
在Rt△PDC中,
∴CP=.
19、答案:见解答
分析:本题考查了旋转的性质、全等三角形的判定与性质.
解答:(1)∵将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,
∴△ABC≌△DBE,
∴∠BAC=∠CDF,
∵∠BAC+∠ACB=90°,
∴∠CDF+∠ACB=90°,
∴DF⊥AC,且点F是AC中点,
∴DF垂直平分AC,
∴AE=CE.
(2)∵△ABC≌△DBE,
∴BE=CE=,
∴CE=AE=2,
∴AB=AE+BE=2+.
20、答案:见解答
分析:本题考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质.
解答:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=A
D.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,∵,
∴△EAB≌△DAC,
∴∠AEB=∠ADC;
(2)如图,∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形,
∴∠AED=60°,
又∵∠AEB=∠ADC=105°,
∴∠BED=105°–60°=45°.
21、答案:见解答
分析:本题考查了旋转的性质、等边三角形的判定与性质、垂线段最短、直角三角形的判定.
解答:(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形,
故答案为:等边.
(2)存在,当6<t<10时,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE=AB+DE=4+DE,
由(1)知,△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,,
∴△BDE的最小周长.
(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,
∴当点D与点B重合时,不符合题意,
②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEB=60°,
∴∠CEB=30°,
∵∠CEB=∠CDA,
∴∠CDA=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA-DA=6-4=2,
∴m=2.
③当6<m<10时,由∠DBE=120°>90°,∴此时不存在.
④当m>10时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14,∴m=14,
综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.
同课章节目录
