北师大版九年级上册数学课件:4.5 相似三角形判定定理的证明课件(共24张PPT)
文档属性
| 名称 | 北师大版九年级上册数学课件:4.5 相似三角形判定定理的证明课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
4.5相似三角形判定定理的证明
?
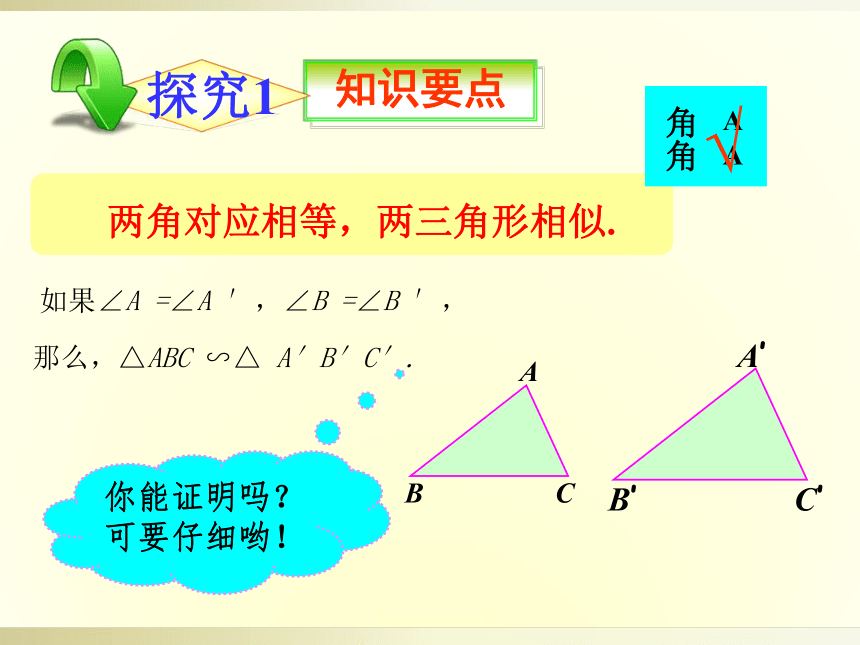
两角对应相等,两三角形相似.
?
三边对应成比例,两三角形相似.
相似三角形的判定方法:
?
两边对应成比例且夹角相等,两三角形相似.
回顾与复习
知识要点
两角对应相等,两三角形相似.
角角
A
A
A′
B′
C′
A
B
C
那么,△ABC
∽△
A′B′C′.
√
如果∠A
=∠A
′,∠B
=∠B
′,
探究1
你能证明吗?可要仔细哟!
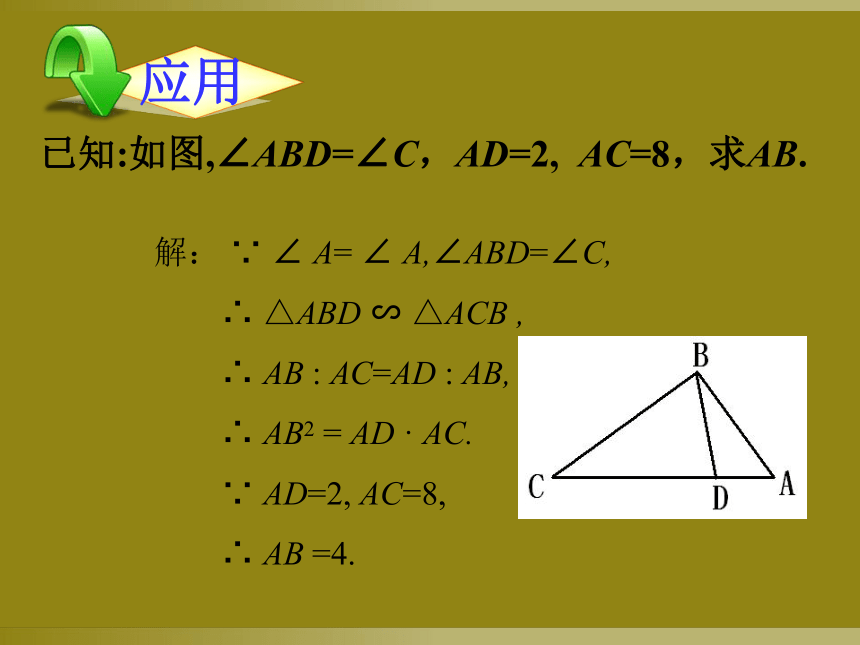
解:
∵
∠
A=
∠
A,∠ABD=∠C,
∴
△ABD
∽
△ACB
,
∴
AB
:
AC=AD
:
AB,
∴
AB2
=
AD
·
AC.
∵
AD=2,
AC=8,
∴
AB
=4.
已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB.
应用
知识要点
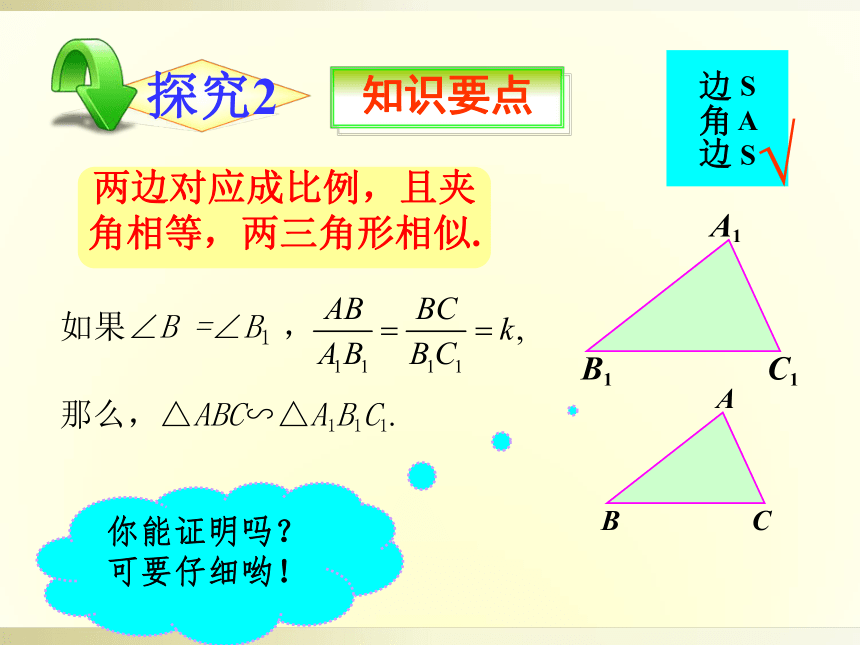
两边对应成比例,且夹角相等,两三角形相似.
边角边
S
A
S
√
A1
B1
C1
A
B
C
那么,△ABC∽△A1B1C1.
如果∠B
=∠B1
,
探究2
你能证明吗?可要仔细哟!
不会
思考
如果
这两个三角形一定会相似吗?
应用
解:(1)
∽
两个三角形的相似比是多少?
已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=
,求AD的长.
解:
AB=6,BC=4,AC=5,CD=
又∠B=∠ACD,
△ABC∽△DCA,
AD=
应用
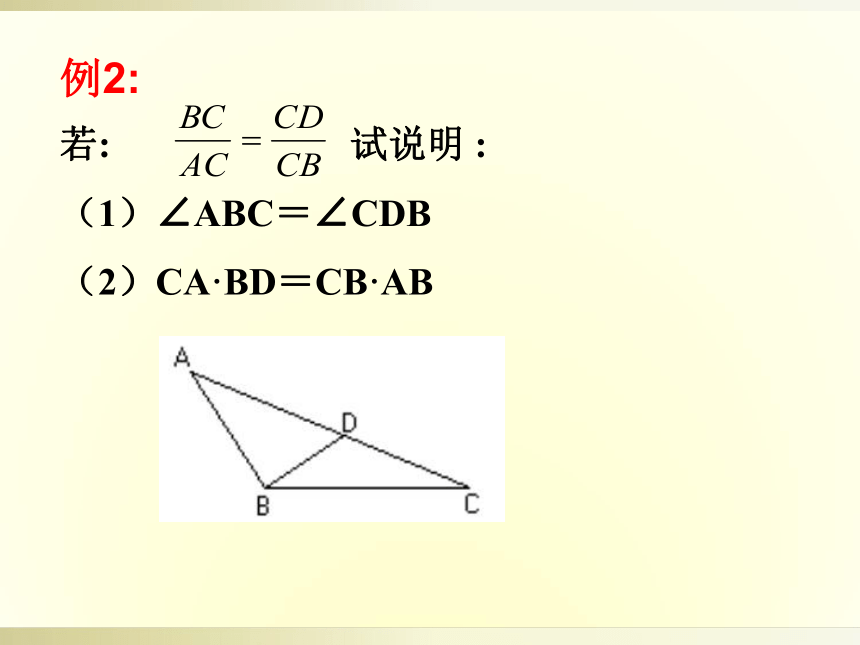
若:
试说明
:
(1)∠ABC=∠CDB
(2)CA·BD=CB·AB
例2:
知识要点
那么,△ABC∽△A′B′C′.
A′
B′
C′
A
B
C
三边对应成比例,两三角形相似.
边边边
S
S
S
√
探究3
如果
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
画一画
求证:
△
.
∽△
A
B
C
D
E
∴
又
∴
同理
∴
∴
∥
∽
∽
∴
∽
∽
例1.下面两个三角形是否相似?为什么?
解:在△ABC和△DEF中.
∴△
ABC
∽
△
ADE.
(三条对应边成比例的两个
三角形相似.)
A
B
C
4cm
7cm
5cm
D
E
F
2cm
2.5cm
3.5cm
四.应用结论,解决问题
如图,△
ABC与△
A′B′C′相似吗?
你用什么方法来支持你的判断?
∴△
ABC∽△
A′B′C′
(三边对应成比例的两个三角形相似.)
C
B
A
A′
B′
C′
解:如图,设小正方形的边长为1,由勾股定理可得:
有一池塘,
周围都是空地.
如果要测量池塘两端A、B间的距离,
你能利用本节所学的知识解决这个问题吗?
?
?
A
B
?
?
?
D
E
C
?
?
2.(选做题)
?
?
C
E
D
?
?
B
A
3.如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°
得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形;
(2)解:BM=MC.
理由如下:∵∠BAM+∠AMB=90°,
∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴
=
,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴
=
,
∴
=
,
∴BM=MC.
Q
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值;
.
解(1)①当△BPQ∽△BAC时,
∵
=
,BP=5t,QC=4t,AB=10cm,BC=8cm,
∴
=
,
∴t=1;
②当△BPQ∽△BCA时,
∵
=
,
∴
,
=
∴t=
,
∴t=1或
时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,
∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且
∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴
=
,
∴
=
,
解得:t=
;
一、相似三角形判定定理的证明
1.两角对应相等,两三角形相似.
3.两边对应成比例且夹角相等,两三角形相似.
二、相似三角形判定定理的应用
2.三边对应成比例,两三角形相似.
小结
习题
知识技能
作业布置
4.5相似三角形判定定理的证明
?
两角对应相等,两三角形相似.
?
三边对应成比例,两三角形相似.
相似三角形的判定方法:
?
两边对应成比例且夹角相等,两三角形相似.
回顾与复习
知识要点
两角对应相等,两三角形相似.
角角
A
A
A′
B′
C′
A
B
C
那么,△ABC
∽△
A′B′C′.
√
如果∠A
=∠A
′,∠B
=∠B
′,
探究1
你能证明吗?可要仔细哟!
解:
∵
∠
A=
∠
A,∠ABD=∠C,
∴
△ABD
∽
△ACB
,
∴
AB
:
AC=AD
:
AB,
∴
AB2
=
AD
·
AC.
∵
AD=2,
AC=8,
∴
AB
=4.
已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB.
应用
知识要点
两边对应成比例,且夹角相等,两三角形相似.
边角边
S
A
S
√
A1
B1
C1
A
B
C
那么,△ABC∽△A1B1C1.
如果∠B
=∠B1
,
探究2
你能证明吗?可要仔细哟!
不会
思考
如果
这两个三角形一定会相似吗?
应用
解:(1)
∽
两个三角形的相似比是多少?
已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=
,求AD的长.
解:
AB=6,BC=4,AC=5,CD=
又∠B=∠ACD,
△ABC∽△DCA,
AD=
应用
若:
试说明
:
(1)∠ABC=∠CDB
(2)CA·BD=CB·AB
例2:
知识要点
那么,△ABC∽△A′B′C′.
A′
B′
C′
A
B
C
三边对应成比例,两三角形相似.
边边边
S
S
S
√
探究3
如果
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
画一画
求证:
△
.
∽△
A
B
C
D
E
∴
又
∴
同理
∴
∴
∥
∽
∽
∴
∽
∽
例1.下面两个三角形是否相似?为什么?
解:在△ABC和△DEF中.
∴△
ABC
∽
△
ADE.
(三条对应边成比例的两个
三角形相似.)
A
B
C
4cm
7cm
5cm
D
E
F
2cm
2.5cm
3.5cm
四.应用结论,解决问题
如图,△
ABC与△
A′B′C′相似吗?
你用什么方法来支持你的判断?
∴△
ABC∽△
A′B′C′
(三边对应成比例的两个三角形相似.)
C
B
A
A′
B′
C′
解:如图,设小正方形的边长为1,由勾股定理可得:
有一池塘,
周围都是空地.
如果要测量池塘两端A、B间的距离,
你能利用本节所学的知识解决这个问题吗?
?
?
A
B
?
?
?
D
E
C
?
?
2.(选做题)
?
?
C
E
D
?
?
B
A
3.如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°
得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形;
(2)解:BM=MC.
理由如下:∵∠BAM+∠AMB=90°,
∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴
=
,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴
=
,
∴
=
,
∴BM=MC.
Q
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值;
.
解(1)①当△BPQ∽△BAC时,
∵
=
,BP=5t,QC=4t,AB=10cm,BC=8cm,
∴
=
,
∴t=1;
②当△BPQ∽△BCA时,
∵
=
,
∴
,
=
∴t=
,
∴t=1或
时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,
∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且
∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴
=
,
∴
=
,
解得:t=
;
一、相似三角形判定定理的证明
1.两角对应相等,两三角形相似.
3.两边对应成比例且夹角相等,两三角形相似.
二、相似三角形判定定理的应用
2.三边对应成比例,两三角形相似.
小结
习题
知识技能
作业布置
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
