华东师大版八年级上册13.2.3边角边课件 (SAS)(20张PPT)
文档属性
| 名称 | 华东师大版八年级上册13.2.3边角边课件 (SAS)(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 20:31:44 | ||
图片预览







文档简介
(共20张PPT)
2.3全等三角形的判定
---边角边(SAS)
华师版八年级上学期
第13章
《全等三角形》
学而不疑则怠,疑而不探则空
若△AOC≌△BOD,
对应边:
AC=
,
AO=
,
CO=
;
对应角:
∠A=
,
∠C=
,
∠AOC=
.
A
B
O
C
D
温故知新:全等三角形的性质
BD
BO
DO
∠B
∠D
∠BOD
思考:如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
上节课给大家留了这样一个思考题,你们想好了吗?
有以下的四种情况:
1、三角;2、两边一角;
3、两角一边;4、三边.
上节课我们已得出结论:三内角对应相等的两个三角形不一定全等.
本节课我们探索:
2、两角一边
探索:如果已知两个三角形有两边一角对应相等时,应分为几种情形讨论?
A
B
C
A'
B'
C'
第一种:
边--角--边
A
B
C
A'
B'
C'
第二种:
边--边--角
作图
画一个三角形,使它的一个内角
为45°,夹这个角的一条边为3厘米,另一条边长为4厘米.
步骤:1.画一线段AB,使它等于4cm;
△ABC就是所求作的三角形.
4cm
A
B
2.画∠MAB=45°;
M
45?
3.在射线AM上截取AC=3cm;
C
3cm
4.连结BC.
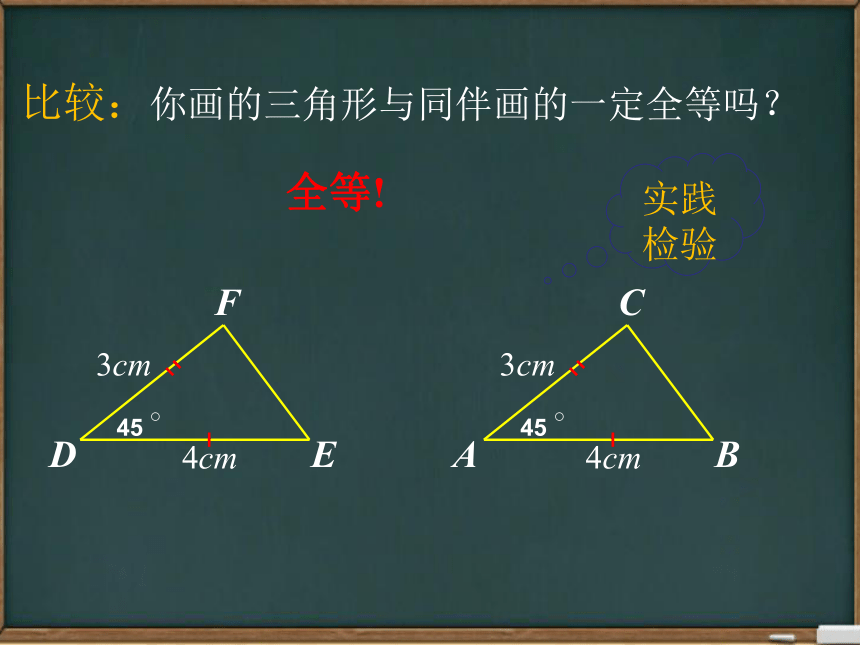
比较:你画的三角形与同伴画的一定全等吗?
实践检验
4cm
3cm
D
E
F
45?
4cm
3cm
A
B
C
45?
全等!
同桌两个同学自行约定:各画一个三角形,使它们具有相同的两条边和一个夹角,比较一下,可以得出什么结论?
实践与探索
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
结论:
温馨提示:
这是一个公理
D
E
F
A
B
C
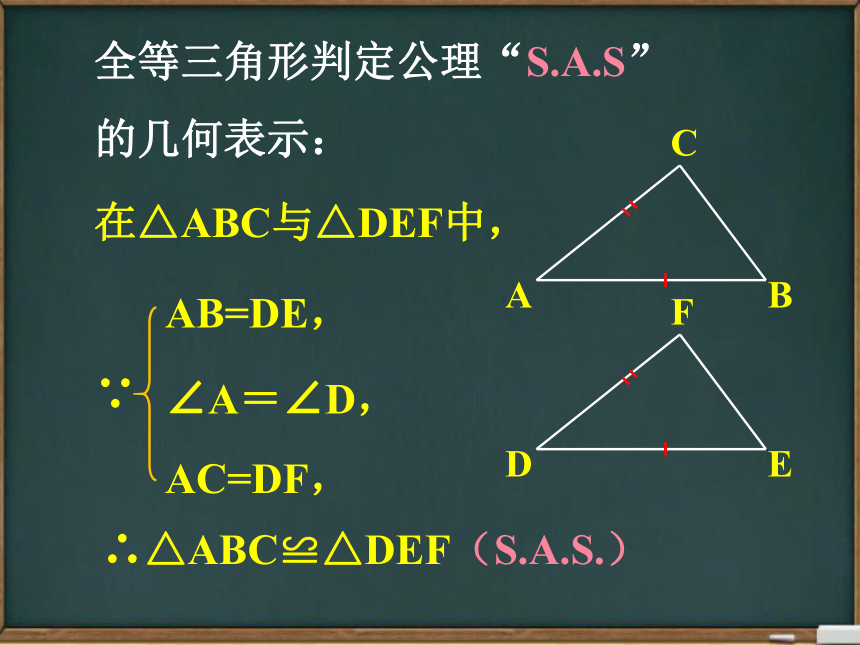
全等三角形判定公理“S.A.S”
的几何表示:
在△ABC与△DEF中,
∵
AB=DE,
∠A=∠D,
AC=DF,
∴△ABC≌△DEF(S.A.S.)
例1:如图,在△ABC中,AB=AC,AD平分∠BAC.
求证:△ABD≌△ACD.
证明:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
∴△ABD≌△ACD(S.A.S.)
∵
A
B
C
D
巩固练习
1.在下列图中找出全等三角形:
Ⅰ
?
30?
8
cm
9
cm
Ⅵ
?
30?
8
cm
8
cm
Ⅳ
8
cm
5
cm
Ⅱ
30?
?
8
cm
5
cm
Ⅴ
30?
8
cm
?
5
cm
Ⅷ
8
cm
5
cm
?
30?
8
cm
9
cm
Ⅶ
Ⅲ
?
30?
8
cm
8
cm
2、如图,已知AB和CD相交于O,
OA=OB,
OC=OD.说明
△OAD与△OBC全等的理由.
OA
=
OB
(已知)
∠1
=∠2
(对顶角相等)
OD
=
OC
(已知)
∴△OAD≌△OBC
(S.A.S)
解:在△OAD
和△OBC中
C
B
A
D
O
2
1
∵
3、如图所示, 根据题目条件,判断下面的
三角形是否全等.
(1)AC=DF,∠C=∠F,BC=EF;
(2)BC=BD,
∠ABC=∠ABD.
A
C
B
F
E
D
C
A
D
B
例2:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH,
ED=FD
,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
解:在△EDH和△FDH中:
ED=FD
(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)
∴△EDH≌△FDH(S.A.S)
∴EH=FH(全等三角形对应边相等)
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
∵
AB
=
A’B’
,∠B
=∠B’
,BC
=B’C’
∴
△
ABC≌
△A’B’C’(S.A.S)
A
B
C
A’
B’
C’
做一做:
以3cm、4cm为三角形的两边,长度3cm的边所对的角为45°
,情况又怎样?动手画一画,你发现了什么?
边边角对应相等的情况又会怎样呢?
探索:
A
B
C
3cm
4cm
45°
3cm
M
B'
步骤:1.画一线段AC,使它等于4cm
;
显然:
△ABC与△AB’C不全等!
4.连结CB、CB'
.
2.画∠CAM=
45?;
3.以C为圆心,
3cm长为半径画弧,
交AM于点B和点B';
△ABC与AB'C就是所求作的三角形.
结论:两边及其一边所对的角相等,
两个三角形不一定全等.
课堂小结
1、边角边公理:有两边和它们的夹角对应
相等的两个三角形全等。(S.A.S)
2、边角边公理的应用中所用到的数学方法:
转化法——要证明线段(或角)相等,
证明线段(或角)所在的两个三角形全等.
课后作业:
1、已知:如图,AB=AC,AD
=
AE
.
求证:△ABE≌△ACD.
B
E
A
C
D
2、如图:己知AD∥BC,AE=CF,AD=BC,
E、F都在直线AC上,试说明DE∥BF。
F
C
B
E
D
A
A
B
D
C
3、如图1:若AB=AC,则添加什么条件可得
△ABD≌△ACD?
4、如图2:若AB=AD,∠1=∠2,则添加什么
条件可得△ABC≌△ADE?
A
B
C
D
E
1
2
2.3全等三角形的判定
---边角边(SAS)
华师版八年级上学期
第13章
《全等三角形》
学而不疑则怠,疑而不探则空
若△AOC≌△BOD,
对应边:
AC=
,
AO=
,
CO=
;
对应角:
∠A=
,
∠C=
,
∠AOC=
.
A
B
O
C
D
温故知新:全等三角形的性质
BD
BO
DO
∠B
∠D
∠BOD
思考:如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
上节课给大家留了这样一个思考题,你们想好了吗?
有以下的四种情况:
1、三角;2、两边一角;
3、两角一边;4、三边.
上节课我们已得出结论:三内角对应相等的两个三角形不一定全等.
本节课我们探索:
2、两角一边
探索:如果已知两个三角形有两边一角对应相等时,应分为几种情形讨论?
A
B
C
A'
B'
C'
第一种:
边--角--边
A
B
C
A'
B'
C'
第二种:
边--边--角
作图
画一个三角形,使它的一个内角
为45°,夹这个角的一条边为3厘米,另一条边长为4厘米.
步骤:1.画一线段AB,使它等于4cm;
△ABC就是所求作的三角形.
4cm
A
B
2.画∠MAB=45°;
M
45?
3.在射线AM上截取AC=3cm;
C
3cm
4.连结BC.
比较:你画的三角形与同伴画的一定全等吗?
实践检验
4cm
3cm
D
E
F
45?
4cm
3cm
A
B
C
45?
全等!
同桌两个同学自行约定:各画一个三角形,使它们具有相同的两条边和一个夹角,比较一下,可以得出什么结论?
实践与探索
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
结论:
温馨提示:
这是一个公理
D
E
F
A
B
C
全等三角形判定公理“S.A.S”
的几何表示:
在△ABC与△DEF中,
∵
AB=DE,
∠A=∠D,
AC=DF,
∴△ABC≌△DEF(S.A.S.)
例1:如图,在△ABC中,AB=AC,AD平分∠BAC.
求证:△ABD≌△ACD.
证明:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
∴△ABD≌△ACD(S.A.S.)
∵
A
B
C
D
巩固练习
1.在下列图中找出全等三角形:
Ⅰ
?
30?
8
cm
9
cm
Ⅵ
?
30?
8
cm
8
cm
Ⅳ
8
cm
5
cm
Ⅱ
30?
?
8
cm
5
cm
Ⅴ
30?
8
cm
?
5
cm
Ⅷ
8
cm
5
cm
?
30?
8
cm
9
cm
Ⅶ
Ⅲ
?
30?
8
cm
8
cm
2、如图,已知AB和CD相交于O,
OA=OB,
OC=OD.说明
△OAD与△OBC全等的理由.
OA
=
OB
(已知)
∠1
=∠2
(对顶角相等)
OD
=
OC
(已知)
∴△OAD≌△OBC
(S.A.S)
解:在△OAD
和△OBC中
C
B
A
D
O
2
1
∵
3、如图所示, 根据题目条件,判断下面的
三角形是否全等.
(1)AC=DF,∠C=∠F,BC=EF;
(2)BC=BD,
∠ABC=∠ABD.
A
C
B
F
E
D
C
A
D
B
例2:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH,
ED=FD
,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
解:在△EDH和△FDH中:
ED=FD
(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)
∴△EDH≌△FDH(S.A.S)
∴EH=FH(全等三角形对应边相等)
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
∵
AB
=
A’B’
,∠B
=∠B’
,BC
=B’C’
∴
△
ABC≌
△A’B’C’(S.A.S)
A
B
C
A’
B’
C’
做一做:
以3cm、4cm为三角形的两边,长度3cm的边所对的角为45°
,情况又怎样?动手画一画,你发现了什么?
边边角对应相等的情况又会怎样呢?
探索:
A
B
C
3cm
4cm
45°
3cm
M
B'
步骤:1.画一线段AC,使它等于4cm
;
显然:
△ABC与△AB’C不全等!
4.连结CB、CB'
.
2.画∠CAM=
45?;
3.以C为圆心,
3cm长为半径画弧,
交AM于点B和点B';
△ABC与AB'C就是所求作的三角形.
结论:两边及其一边所对的角相等,
两个三角形不一定全等.
课堂小结
1、边角边公理:有两边和它们的夹角对应
相等的两个三角形全等。(S.A.S)
2、边角边公理的应用中所用到的数学方法:
转化法——要证明线段(或角)相等,
证明线段(或角)所在的两个三角形全等.
课后作业:
1、已知:如图,AB=AC,AD
=
AE
.
求证:△ABE≌△ACD.
B
E
A
C
D
2、如图:己知AD∥BC,AE=CF,AD=BC,
E、F都在直线AC上,试说明DE∥BF。
F
C
B
E
D
A
A
B
D
C
3、如图1:若AB=AC,则添加什么条件可得
△ABD≌△ACD?
4、如图2:若AB=AD,∠1=∠2,则添加什么
条件可得△ABC≌△ADE?
A
B
C
D
E
1
2
