华东师大版八年级上册13.3.1等腰三角形的性质课件(共19张PPT)
文档属性
| 名称 | 华东师大版八年级上册13.3.1等腰三角形的性质课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 20:37:33 | ||
图片预览






文档简介
(共19张PPT)
3.1等腰三角形的性质
华师版八年级上学期
第13章
《全等三角形》
学而不疑则怠,疑而不探则空
知识回顾
一、基本概念
1.定义:
两条边相等的三角形叫做等腰三角形.
如图:AB=AC,?ABC就是等腰三角形.
A
B
C
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做底(边)
底
两腰的夹角叫做顶角
顶角
腰和底边的夹角叫做底角
底角
腰
腰
底角
A
B
C
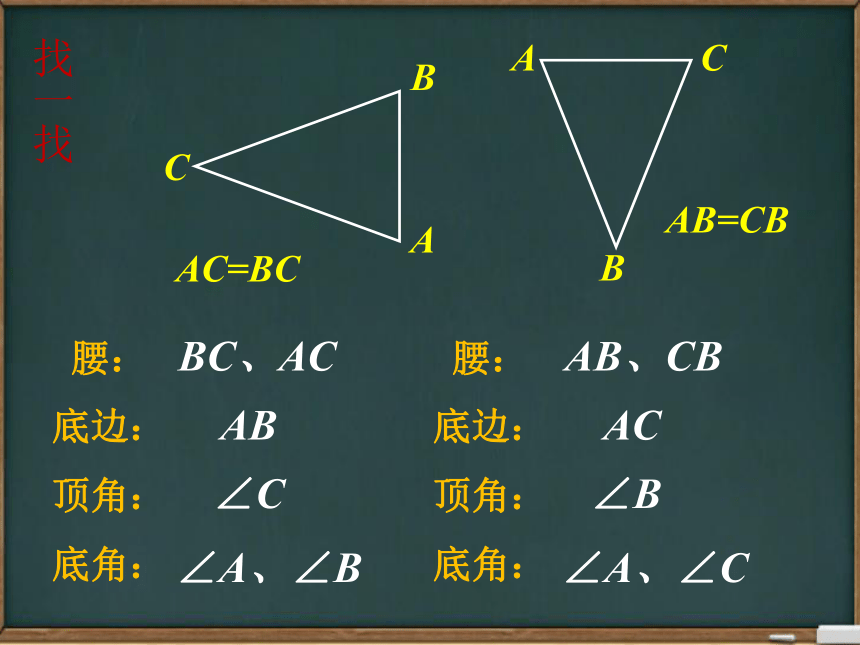
AC=BC
腰:
底边:
顶角:
底角:
A
B
C
AB=CB
找一找
BC、AC
AB
∠C
∠A、∠B
腰:
底边:
顶角:
底角:
AB、CB
AC
∠B
∠A、∠C
二、等腰三角形性质的探索
A
B
C
操作:将?ABC对折,使两腰AB、AC重叠在一起,折痕为AD.
D
观察:
你发现了什么?
重合的线段:
AB=AC
BD=CD
∠B=∠C
∠BAD=∠CAD
重合的角:
∠ADB=∠ADC
思考:除了两腰相等,
等腰三角形还
有哪些性质?
归纳:
A
B
C
D
1、等腰三角形是轴对称图形,
AD所在直线是对称轴;
2、∠B=∠C;
3、BD=CD,AD是底边的中线;
4、∠BAD=∠CAD,AD是顶角平分线;
5、∠ADB=∠ADC=90°,AD是底边上的高.
其中,“∠B=∠C”用文字如何表述?
A
B
C
等腰三角形的两底角相等.
(简称为“等边对等角”)
已知:如图,?ABC中,AB=AC.
求证:∠B=∠C.
D
证明:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
AB=AC,
AD=AD
∴
Rt△ADB≌Rt△ADC
(H.L.)
∴
∠B=∠C.
定理:
分析:要证明两角相等,通常先证明这两个角所在的两个三角形全等,此题需要添加辅助线构造全等三角形.
A
B
C
已知:如图,?ABC中,AB=AC.
求证:∠B=∠C.
E
法二:作∠BAC的平分线AE交BC点E,
则∠BAE=∠CAE.
在△AEB和△AEC中,
AB=AC,
∠BAE=∠CAE,
AE=AE
∴
△AEB≌△AEC
(S.A.S.)
∴
∠B=∠C.
A
B
C
已知:如图,?ABC中,AB=AC.
求证:∠B=∠C.
F
法三:作BC的中线AF交BC点F,
则BF=CF.
在△AFB和△AFC中,
AB=AC,
BF=CF,
AF=AF
∴
△AFB≌△AFC
(S.S.S.)
∴
∠B=∠C.
归纳:
A
B
C
D
1、等腰三角形是轴对称图形,
AD所在直线是对称轴;
2、∠B=∠C;
3、BD=CD,AD是底边的中线;
4、∠BAD=∠CAD,AD是顶角平分线;
5、∠ADB=∠ADC=90°,AD是底边上的高.
其中3、4、5用一句话可以归纳为什么?
等边对等角
等腰三角形的顶角平分线、底边上的高、底边的中线互相重合.(简称“三线合一”)
A
B
C
注意
“等腰三角形”是三线合一的大前提;
一定要明确是哪三线.
A
B
C
用几何语言表示等腰三角形的性质
在?ABC中,∵AB=AC,
∴∠B=∠C.(等边对等角)
在?ABC中,AB=AC时,
D
(1)
∵AD是BC的高,
∴∠BAD=∠CAD,BD=CD.(三线合一)
(2)
∵AD是BC的中线,
∴∠BAD=∠CAD,AD⊥BC.(三线合一)
(3)
∵AD是∠BAC的平分线,
∴BD=CD,AD⊥BC.(三线合一)
判断下列命题是否正确:
1、等腰三角形的角平分线、中线和高
互相重合.
(
)
2、有一个角是60°的等腰三角形,其余
两个内角也是60°.
(
)
3、等腰三角形的底角都是锐角.
(
)
4、钝角三角形不可能是等腰三角形.
(
)
错
对
错
对
及时反馈
1、等腰三角形的一个角是70°,它的另外两个角为
.
2、等腰三角形的一个角是110°,它的另外两个角为
.
3、等腰三角形有两边长是4和7,则它的周长为
.
70°,40°或55°,55°
35°,35°
15或18
4、等腰三角形有两边长是3和7,则它的周长为
.
17
及时反馈
1.已知在?ABC中,AB=AC,
∠C=80°,求∠A和∠B的度数.
A
B
C
解:∵AB=AC,
∴∠B=∠C=80°.
(等边对等角)
∵∠A+∠B+∠C=180°,
∴∠A=180°-80°-80°=20°
例题解析
2.如图,在?ABC中,AB=AC,D是BC边的中点,∠B=30°,求∠ADC和∠1的度数.
解:∵AB=AC且D是BC边的中点,
∴AD是∠BAC的平分线及BC边的高.
(三线合一)
∵∠1+∠B=∠ADC,
∴∠ADC=90°
∠B=30°,
∴∠1=90°-30°=60°
A
B
C
D
1
三、等边三角形
A
B
C
1、定义:三条边都相等的三角形叫等边三角形(或正三角形).
如图,∠A=∠B=∠C=60°.
如图,AB=BC=AC,
?ABC是等边三角形.
三条边都相等.
2、等边三角形的性质:
三个角都相等,都等于60°.
如图,AB=BC=AC.
1、等腰三角形的性质:
(1)等边对等角.
(2)等腰三角形的顶角平分线、底边上的高、底边的中线互相重合.
(简称“三线合一”)
“三线合一”性质在实际应用中,只要其中一个结论成立,另外两个一定成立。
2、等边三角形的性质:
三条边相等;三个角都是60°.
知识小结
1、如图,在△ABC中,AB=AC,D是BC边上的中点,DE⊥AB于E,
DF⊥
AC于F。求证:DE=DF.
课后作业
A
E
D
C
B
F
2、如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。
求证:AH=2BD.
A
E
D
C
B
H
3.1等腰三角形的性质
华师版八年级上学期
第13章
《全等三角形》
学而不疑则怠,疑而不探则空
知识回顾
一、基本概念
1.定义:
两条边相等的三角形叫做等腰三角形.
如图:AB=AC,?ABC就是等腰三角形.
A
B
C
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做底(边)
底
两腰的夹角叫做顶角
顶角
腰和底边的夹角叫做底角
底角
腰
腰
底角
A
B
C
AC=BC
腰:
底边:
顶角:
底角:
A
B
C
AB=CB
找一找
BC、AC
AB
∠C
∠A、∠B
腰:
底边:
顶角:
底角:
AB、CB
AC
∠B
∠A、∠C
二、等腰三角形性质的探索
A
B
C
操作:将?ABC对折,使两腰AB、AC重叠在一起,折痕为AD.
D
观察:
你发现了什么?
重合的线段:
AB=AC
BD=CD
∠B=∠C
∠BAD=∠CAD
重合的角:
∠ADB=∠ADC
思考:除了两腰相等,
等腰三角形还
有哪些性质?
归纳:
A
B
C
D
1、等腰三角形是轴对称图形,
AD所在直线是对称轴;
2、∠B=∠C;
3、BD=CD,AD是底边的中线;
4、∠BAD=∠CAD,AD是顶角平分线;
5、∠ADB=∠ADC=90°,AD是底边上的高.
其中,“∠B=∠C”用文字如何表述?
A
B
C
等腰三角形的两底角相等.
(简称为“等边对等角”)
已知:如图,?ABC中,AB=AC.
求证:∠B=∠C.
D
证明:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
AB=AC,
AD=AD
∴
Rt△ADB≌Rt△ADC
(H.L.)
∴
∠B=∠C.
定理:
分析:要证明两角相等,通常先证明这两个角所在的两个三角形全等,此题需要添加辅助线构造全等三角形.
A
B
C
已知:如图,?ABC中,AB=AC.
求证:∠B=∠C.
E
法二:作∠BAC的平分线AE交BC点E,
则∠BAE=∠CAE.
在△AEB和△AEC中,
AB=AC,
∠BAE=∠CAE,
AE=AE
∴
△AEB≌△AEC
(S.A.S.)
∴
∠B=∠C.
A
B
C
已知:如图,?ABC中,AB=AC.
求证:∠B=∠C.
F
法三:作BC的中线AF交BC点F,
则BF=CF.
在△AFB和△AFC中,
AB=AC,
BF=CF,
AF=AF
∴
△AFB≌△AFC
(S.S.S.)
∴
∠B=∠C.
归纳:
A
B
C
D
1、等腰三角形是轴对称图形,
AD所在直线是对称轴;
2、∠B=∠C;
3、BD=CD,AD是底边的中线;
4、∠BAD=∠CAD,AD是顶角平分线;
5、∠ADB=∠ADC=90°,AD是底边上的高.
其中3、4、5用一句话可以归纳为什么?
等边对等角
等腰三角形的顶角平分线、底边上的高、底边的中线互相重合.(简称“三线合一”)
A
B
C
注意
“等腰三角形”是三线合一的大前提;
一定要明确是哪三线.
A
B
C
用几何语言表示等腰三角形的性质
在?ABC中,∵AB=AC,
∴∠B=∠C.(等边对等角)
在?ABC中,AB=AC时,
D
(1)
∵AD是BC的高,
∴∠BAD=∠CAD,BD=CD.(三线合一)
(2)
∵AD是BC的中线,
∴∠BAD=∠CAD,AD⊥BC.(三线合一)
(3)
∵AD是∠BAC的平分线,
∴BD=CD,AD⊥BC.(三线合一)
判断下列命题是否正确:
1、等腰三角形的角平分线、中线和高
互相重合.
(
)
2、有一个角是60°的等腰三角形,其余
两个内角也是60°.
(
)
3、等腰三角形的底角都是锐角.
(
)
4、钝角三角形不可能是等腰三角形.
(
)
错
对
错
对
及时反馈
1、等腰三角形的一个角是70°,它的另外两个角为
.
2、等腰三角形的一个角是110°,它的另外两个角为
.
3、等腰三角形有两边长是4和7,则它的周长为
.
70°,40°或55°,55°
35°,35°
15或18
4、等腰三角形有两边长是3和7,则它的周长为
.
17
及时反馈
1.已知在?ABC中,AB=AC,
∠C=80°,求∠A和∠B的度数.
A
B
C
解:∵AB=AC,
∴∠B=∠C=80°.
(等边对等角)
∵∠A+∠B+∠C=180°,
∴∠A=180°-80°-80°=20°
例题解析
2.如图,在?ABC中,AB=AC,D是BC边的中点,∠B=30°,求∠ADC和∠1的度数.
解:∵AB=AC且D是BC边的中点,
∴AD是∠BAC的平分线及BC边的高.
(三线合一)
∵∠1+∠B=∠ADC,
∴∠ADC=90°
∠B=30°,
∴∠1=90°-30°=60°
A
B
C
D
1
三、等边三角形
A
B
C
1、定义:三条边都相等的三角形叫等边三角形(或正三角形).
如图,∠A=∠B=∠C=60°.
如图,AB=BC=AC,
?ABC是等边三角形.
三条边都相等.
2、等边三角形的性质:
三个角都相等,都等于60°.
如图,AB=BC=AC.
1、等腰三角形的性质:
(1)等边对等角.
(2)等腰三角形的顶角平分线、底边上的高、底边的中线互相重合.
(简称“三线合一”)
“三线合一”性质在实际应用中,只要其中一个结论成立,另外两个一定成立。
2、等边三角形的性质:
三条边相等;三个角都是60°.
知识小结
1、如图,在△ABC中,AB=AC,D是BC边上的中点,DE⊥AB于E,
DF⊥
AC于F。求证:DE=DF.
课后作业
A
E
D
C
B
F
2、如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。
求证:AH=2BD.
A
E
D
C
B
H
