人教版七年级上数学1.4.1有理数的乘法法则课件(22张)
文档属性
| 名称 | 人教版七年级上数学1.4.1有理数的乘法法则课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 360.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览





文档简介
问题的提出
在一条东西走向的马路(东为正,西为负)上小明的运动如下所示:
1.向东走,每次3米,走2次;
2.向西走,每次3米,走2次;
3.向东走,每次3米,反方向走2次;
4.向西走,每次3米,反方向走2次;
5.向东走,每次3米,走0次;
6.向西走,每次3米,走0次;
问题:那么他现在位于原来位置的哪个方向?相距多少米?
我的解释:
1.向东走,每次3米,走2次;
这个问题用乘法来解答为:
我的数轴表示:
我的解释:
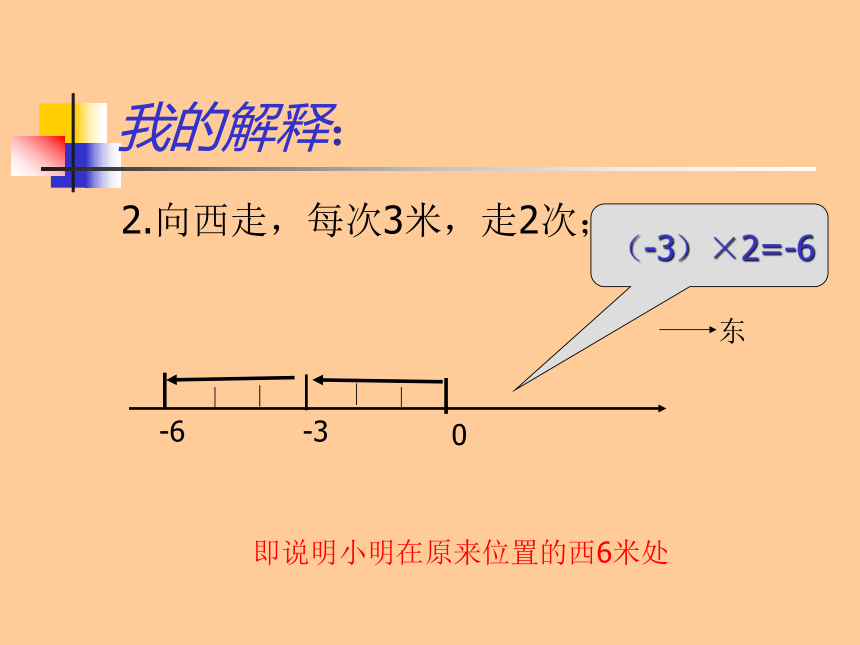
2.向西走,每次3米,走2次;
我的解释:
我的解释:
我的解释:
我的解释:
得出有理数乘法法则:
感受法则、理解法则
若均用 或 表示是相同符号的数相乘的话,请判断下面几种图形相乘所得到的图形结果。
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-5)×(-2)
感受法则、理解法则:
再例如计算(-6)×4
例题学习
计算:
①(-5)×(-6); ②
试试你自己
3×(-2)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
课堂小结
1)有理数的乘法法则。
小测
1.写出下列各数的倒数:
1.5 -2/3 0.3 -4
2.2X(-5/12)= (-4/5)X(-5/4)=
2/3X(-1/5)= (-10)X(-1/5)=
0X(-4)=
3.已知一个数的倒数的相反数是16/5,则这个数是( )
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
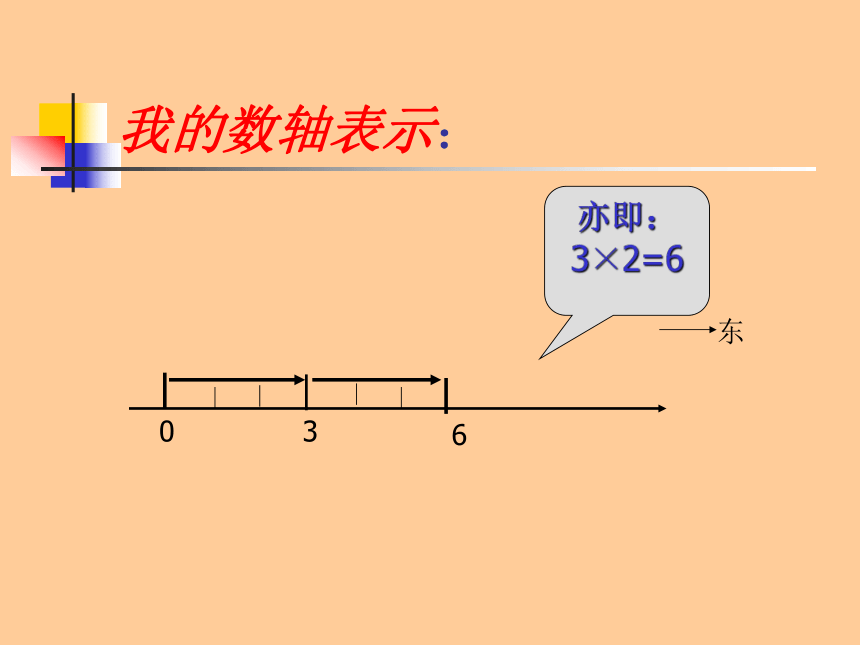
3×2=6
即小明位于原来位置的东方6米处
能用数轴表示这一事实么?动手画一画吧。
0
3
6
东
亦即:3×2=6
-6
-3
0
东
(-3)×2=-6
即说明小明在原来位置的西6米处
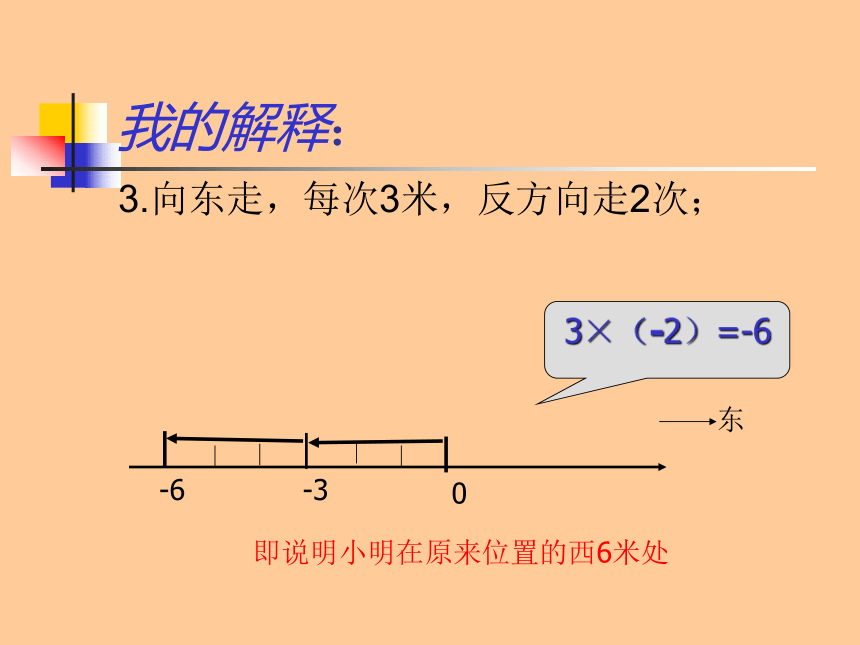
-6
-3
0
东
3×(-2)=-6
3.向东走,每次3米,反方向走2次;
即说明小明在原来位置的西6米处
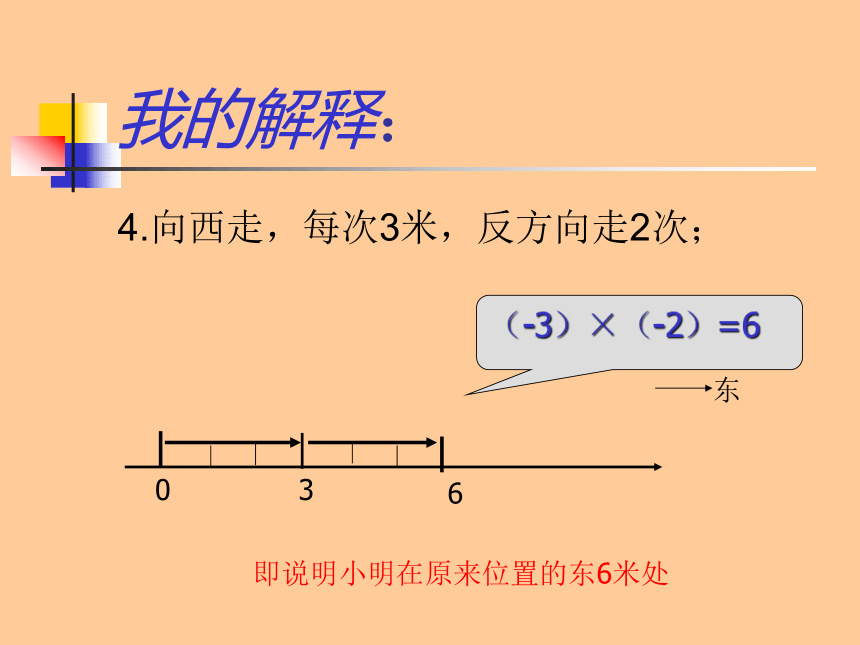
0
3
6
东
(-3)×(-2)=6
4.向西走,每次3米,反方向走2次;
即说明小明在原来位置的东6米处
-3
0
3
东
3×0=0
5.向东走,每次3米,走0次;
即说明小明在原来位置没动
-3
0
3
东
(-3)×0=0
6.向西走,每次3米,走0次;
即说明小明在原来位置没动
2×(-3)=-6
3×2=6
(-2)×(-3)=6
3×0=0
(-2)×3=-6
(-3)×0=0
观察下边的算式,你有什么发现?
同号得正
异号得负
任何数同0相乘,都得0
并把绝对值相乘
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0。
注意:先确定积的符号,再确定积的绝对值。
+
-
+
-
×
=
+
+
+
-
-
-
×
×
×
=
=
=
-
+
-
+
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-5)×(-2)=+( )的判断
三,把绝对值相乘,得出结果。
所以有
(-5)×(-2)=+(10)的结果
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-6)×4= -( )的判断
三,把绝对值相乘,得出结果。
所以有
(-6)×4= -(24)的结果
解: (-5)×(-6)
解:
=+( 5×6)
=30
(-5)×2=
3×(-4)=
-6
-10
-12
一般的,把一个因数换成它的相反数,所得的积是原来积的相反数。
3 × 2 =
(-5)×(-2)=
3 × 4 =
6
10
12
乘积是1的两个数互为倒数;任何数同1相乘,结果仍得原数;任何数同(-1)相乘,得原数的相反数。
计算
5×1
5×(-1)
= ×2
= 1
=5
=-5
计算:
解:原式=
=
这个解答正确么?你认为应该怎么做?答案是多少呢?
1)如果a×b=0,则这两个数 ( )
A 都等于0,
B 有一个等于0,另一个不等于0;
C 至少有一个等于0, D 互为相反数
2)已知-3a是一个负数,则 ( )
A a>0 B a<0 C a≥0 D a≤0
C
A
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
(-7)X8
X
X
X(-0.75)
(-4)X[+(+ )]
4)
2)特殊的乘法运算,任何数同0相乘都得0,乘积是1的两个数互为倒数;任何数同1得它本身,或者与(-1)相乘得它的相反数。
3)我们在进行乘法运算的时候,应该注意些什么呢?
先确定积的符号,再确定积的绝对值。
在一条东西走向的马路(东为正,西为负)上小明的运动如下所示:
1.向东走,每次3米,走2次;
2.向西走,每次3米,走2次;
3.向东走,每次3米,反方向走2次;
4.向西走,每次3米,反方向走2次;
5.向东走,每次3米,走0次;
6.向西走,每次3米,走0次;
问题:那么他现在位于原来位置的哪个方向?相距多少米?
我的解释:
1.向东走,每次3米,走2次;
这个问题用乘法来解答为:
我的数轴表示:
我的解释:
2.向西走,每次3米,走2次;
我的解释:
我的解释:
我的解释:
我的解释:
得出有理数乘法法则:
感受法则、理解法则
若均用 或 表示是相同符号的数相乘的话,请判断下面几种图形相乘所得到的图形结果。
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-5)×(-2)
感受法则、理解法则:
再例如计算(-6)×4
例题学习
计算:
①(-5)×(-6); ②
试试你自己
3×(-2)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
课堂小结
1)有理数的乘法法则。
小测
1.写出下列各数的倒数:
1.5 -2/3 0.3 -4
2.2X(-5/12)= (-4/5)X(-5/4)=
2/3X(-1/5)= (-10)X(-1/5)=
0X(-4)=
3.已知一个数的倒数的相反数是16/5,则这个数是( )
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
3×2=6
即小明位于原来位置的东方6米处
能用数轴表示这一事实么?动手画一画吧。
0
3
6
东
亦即:3×2=6
-6
-3
0
东
(-3)×2=-6
即说明小明在原来位置的西6米处
-6
-3
0
东
3×(-2)=-6
3.向东走,每次3米,反方向走2次;
即说明小明在原来位置的西6米处
0
3
6
东
(-3)×(-2)=6
4.向西走,每次3米,反方向走2次;
即说明小明在原来位置的东6米处
-3
0
3
东
3×0=0
5.向东走,每次3米,走0次;
即说明小明在原来位置没动
-3
0
3
东
(-3)×0=0
6.向西走,每次3米,走0次;
即说明小明在原来位置没动
2×(-3)=-6
3×2=6
(-2)×(-3)=6
3×0=0
(-2)×3=-6
(-3)×0=0
观察下边的算式,你有什么发现?
同号得正
异号得负
任何数同0相乘,都得0
并把绝对值相乘
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0。
注意:先确定积的符号,再确定积的绝对值。
+
-
+
-
×
=
+
+
+
-
-
-
×
×
×
=
=
=
-
+
-
+
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-5)×(-2)=+( )的判断
三,把绝对值相乘,得出结果。
所以有
(-5)×(-2)=+(10)的结果
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-6)×4= -( )的判断
三,把绝对值相乘,得出结果。
所以有
(-6)×4= -(24)的结果
解: (-5)×(-6)
解:
=+( 5×6)
=30
(-5)×2=
3×(-4)=
-6
-10
-12
一般的,把一个因数换成它的相反数,所得的积是原来积的相反数。
3 × 2 =
(-5)×(-2)=
3 × 4 =
6
10
12
乘积是1的两个数互为倒数;任何数同1相乘,结果仍得原数;任何数同(-1)相乘,得原数的相反数。
计算
5×1
5×(-1)
= ×2
= 1
=5
=-5
计算:
解:原式=
=
这个解答正确么?你认为应该怎么做?答案是多少呢?
1)如果a×b=0,则这两个数 ( )
A 都等于0,
B 有一个等于0,另一个不等于0;
C 至少有一个等于0, D 互为相反数
2)已知-3a是一个负数,则 ( )
A a>0 B a<0 C a≥0 D a≤0
C
A
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
(-7)X8
X
X
X(-0.75)
(-4)X[+(+ )]
4)
2)特殊的乘法运算,任何数同0相乘都得0,乘积是1的两个数互为倒数;任何数同1得它本身,或者与(-1)相乘得它的相反数。
3)我们在进行乘法运算的时候,应该注意些什么呢?
先确定积的符号,再确定积的绝对值。
